
Вписывание тележки подвижного состава в кривую
.pdf3.3 Динамическое вписывание экипажа в кривую
Динамическое вписывание предполагает движение в кривой на магистральных участках пути. Радиусы кривых при этом достаточно большие по сравнению с радиусами кривых на тракционных и деповских путях. Развиваемые в кривых большие скорости движения обусловливают появление больших центробежных сил, которые могут вызвать нарушение поперечной устойчивости, всползание гребня направляющего колеса на рельс, поперечный сдвиг рельсо-шпальной решетки, отрыв подошвы наружного рельса от шпалы. Причиной нарушения комфортных условий для пассажиров и локомотивных бригад могут быть большие ускорения, причиной которых также являются центробежные силы. Поэтому конечной целью исследований динамического вписывания является определение максимальной скорости движения, при которой еще обеспечивается безопасность и соответствующий комфорт пассажиров.
Для расчета максимально допустимой скорости движения в кривой прежде всего необходимо найти зависимость бокового давления гребня направляющего колеса на рельс (или рельса на гребень колеса) от скорости движения. Задача эта достаточно сложная и требует громоздких вычислений, поэтому для упрощения расчетов принимаются следующие допущения:
–подвижной состав работает в режиме выбега;
–отсутствует сочленение между тележками;
–пренебрегают влиянием конусности бандажей;
–вертикальные давления колес на рельсы при движении остаются постоянными и равными давлениям в статическом состоянии;
–коэффициент трения между колесом и рельсом не зависит от скорости движения и равен 0,25;
–все силы, действующие на экипаж, находятся в горизонтальной плоскости на уровне головок рельсов;
–отсутствует поперечное отжатие наружного рельса, т. е. путь абсолютно жесткий;
–между кузовом и тележками отсутствуют силы, препятствующие повороту их друг относительно друга;
40

– не учитывается влияние упругих связей колесных пар с рамой тележки.
С учетом перечисленных допущений на рисунке 3.5 приведена расчетная схема вписывания трехосной тележки.
Y |
|
|
Пf |
Пf |
Y |
V |
3 |
|
|
|
|
1 |
|
Пf |
Ω |
α2 |
C |
α1 |
|
|
α3 |
|
Пf |
Пf |
|
||
|
|
|
|
2s |
Пf
xс
x3 x2
x1
2a
Рисунок 3.5 – Вписывание трехосной тележки
На этой схеме:
Y1 – направляющее усилие, действующее на первую колесную пару;
Y3 – боковое усилие от рельса на третью колесную пару; П – вертикальное давление колеса на рельс;
Пf – сила трения между колесом и рельсом;
C– центробежная сила от массы экипажа, приходящейся на одну тележку;
Ω– полюс поворота тележки;
2s – расстояние между кругами катания бандажей, принимаемое в расчетах равным 1,6 м;
xс – расстояние от центра тяжести экипажа до полюса поворота;
x1 , x2 , x3 – расстояние от полюса поворота до первой, второй и третьей колесной пары соответственно.
Величина центробежной силы, приложенной к центру тяжести эки-
пажа
41

C = P( |
V 2 |
− |
h |
) , |
(3.20) |
gR |
2s |
||||
|
д |
|
|
|
|
где P – масса экипажа, приходящаяся на одну тележку; Rд – радиус кривой;
V – скорость движения;
h – возвышение наружного рельса над внутренним;
g– ускорение свободного падения.
Из уравнения (3.20) скорость движения равна
V = |
gCR |
ghR |
|
P д + |
2s д . |
(3.21) |
Как известно, для нахождения полюса поворота из центра кривой опускают перпендикуляр на продольную ось тележки. При достаточно большой скорости движения передние и задние колесные пары тележки будут касаться наружного рельса и точка Ω пересечения перпендикуляра с продольной осью совпадает с центром тяжести экипажа, и тележка займет
так называемое хордовое положение, для которого xc = 0 . В другом крайнем положении тележки, называемом наибольшим перекосом, передняя колесная пара касается наружного рельса, а задняя – внутреннего рельса. Расстояние от центра тяжести или середины экипажа до полюса поворота в этом случае равно
xc = xснп = |
( 2σ+ )Rд |
. |
(3.22) |
|
|||
|
2a |
|
|
Движение экипажа в кривой будем рассматривать в виде двух составляющих движения, одна из которых направлена вдоль касательной к средней окружности пути в кривой. Вторая составляющая представляет собой поворот тележки относительно полюса Ω или мгновенного центра, который происходит под действием усилий Y1 , Y3 и центробежной силы C . В точках контакта колес с рельсами появляются при этом силы трения Пf , препятствующие повороту тележки вокруг мгновенного центра.
Зависимость боковых давлений от скорости движения может быть найдена на основе решения уравнений, составленных применительно к расчетной схеме на рисунке 3.5.
42

Тележка находится в равновесии, если сумма проекций сил на вертикальную ось равна нулю, т. е.
|
Y1 Y3 −C −2Пf cosα1 −2Пf cosα2 2Пf cosα3 = 0 . |
(3.23) |
|||||
|
Кроме того, сумма моментов сил, действующих на тележку, относи- |
||||||
тельно полюса поворота тоже должна быть равна нулю. |
|
|
|
||||
Y x |
Y x |
−Cx −2Пf |
x2 + s2 −2Пf |
x2 + s2 −2Пf |
x2 |
+ s2 =0 |
. (3.24) |
1 1 |
3 3 |
c |
1 |
2 |
3 |
|
|
|
Эти уравнения содержат четыре неизвестных Y1 , |
Y3 , |
C и xc . Значе- |
||||
ния двух «лишних» неизвестных, а именно Y3 и xc могут быть найдены до решения системы уравнений. Действительно, в двух крайних положениях тележки, хордовом и положении наибольшего перекоса, значения xc , как уже отмечалось, определяются достаточно просто. Если предположить, что в этих положениях тележки гребень бандажа задней колесной пары лишь касается рельса, не оказывая при этом бокового давления, можно принять Y3 = 0 . Таким образом, в исходных уравнениях останутся неизвестными
только Y1 и C . Входящие в уравнениях(3.23) |
значения косинусов углов |
|||
определяются |
|
|
|
|
cosαi = |
xi |
. |
(3.25) |
|
x2 + s2 |
||||
|
|
|
||
|
i |
|
|
|
При расположении тележки в промежуточных положениях Y3 |
всегда |
|||
равен нулю, значение же xc будут находиться в пределах от нуля до
xснп (уравнение 3.22). Принимая, например, xc = 0,25xснп, xc =0,5xснп и т. д. и решая совместно уравнения (3.23) и (3.24), можно найти Y1 и C для промежуточных положений тележки в кривой. Зная величину центробежной силы по формуле (3.21), находим скорость движения экипажа в кривой с учетом и без учета возвышения наружного рельса над внутренним. Расчет динамического вписывания удобно выполнять в форме таблицы 3.1.
43

Таблица 3.1 – Расчет динамического вписывания |
|
|
||||||
Расчетная |
|
|
Значения xc ,м |
|
|
|||
|
величина |
0 xснп |
0,25 xснп |
0,5 xснп 0,75 xснп 1 xснп |
||||
|
|
|
|
|||||
|
|
1 |
|
2 |
3 |
4 |
5 |
6 |
x1, м |
|
|
|
|
|
|
|
|
x2 , м |
|
|
|
|
|
|
|
|
x3, м |
|
|
|
|
|
|
|
|
x2 |
+ s2 |
, м |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x22 + s2 , м |
|
|
|
|
|
|||
x2 +s2 |
, м |
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
cosα1 |
= |
x1 |
|
|
|
|
|
|
|
+ s2 |
|
|
|
|
|
||
|
x2 |
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
cosα2 |
= |
x2 |
|
|
|
|
|
|
|
+ s2 |
|
|
|
|
|
||
|
x2 |
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2Пf ∑cosαi , кН |
|
|
|
|
|
|||
i=1 |
|
|
|
|
|
|
|
|
3 |
|
+ s2 , кНм |
|
|
|
|
||
2Пf ∑ x2 |
|
|
|
|
||||
|
i |
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
Y1 , кН |
|
|
|
|
|
|
|
|
C , кН |
|
|
|
|
|
|
|
|
V , км |
h = 0 |
|
|
|
|
|
||
h > 0 |
|
|
|
|
|
|||
ч |
|
|
|
|
|
|||
|
Используя найденные значения, строим кривые зависимостей боко- |
|||||||
вых давлений Y1 |
рельса на гребень первой направляющей колесной пары |
|||||||
от скорости движения V экипажа (рисунок 3.6). |
|
|
||||||
|
Определение максимально допустимой по условиям всползания |
|||||||
гребня на рельс скорости движения является завершающим этапом иссле- |
||||||||
дований динамического вписывания экипажа в кривую. |
|
|
||||||
44
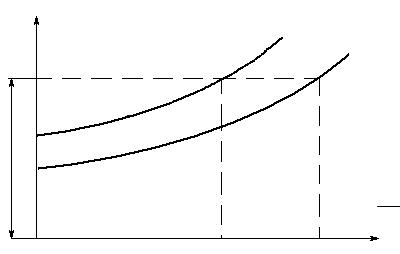
Y1,кН |
h =0 |
h >0 |
|
Y1max
V , кмч
V1max V2 max
Рисунок 3.6 – Зависимости боковых давлений рельса от скорости движения экипажа
Критерием устойчивости против схода с рельсов вследствие всползания гребня на рельс является отношение
Y1max |
≤(1,1....1,3 ), |
(3.26) |
П |
|
|
Y1max ≤(1,1....1,3 ) П. |
(3.27) |
|
Отложив по вертикальной оси Y1max (рисунок 3.6), графически на-
ходим Y1max без учета возвышения наружного рельса над внутренним и
V2 max – с учетом возвышения. Найденные значения скоростей должны быть выше конструкционной скорости движения. В противном случае необходимо принять меры, исключающие всползание гребней направляющих колесных пар на рельс.
К таким мерам можно отнести применение:
–оптимального возвышения наружного рельса над внутренним;
–упругих межтележечных сочленений;
–упругих связей колесных пар с рамами тележек (поводковые буксы
ибуксы с цилиндрическими направляющими);
–принудительного наклона кузова на подвижном составе, оборудованном пневматическими рессорами.
45
Контрольные вопросы
1.Как отличаются ощущения пассажиров при движении с одной и той же скоростью в кривой с возвышением наружного рельса и без него?
2.Какова специфика износа бандажей локомотивов с одним преимущественным направлением кривых малого радиуса?
3.Как изменится полюсное расстояние, если тележка при неизменной скорости въедет на участок с замасленными рельсами?
4.Почему после смены балласта ограничивают скорость движения подвижного состава?
5.Для чего поводки на буксах располагают на разных уровнях?
46
Список использованных источников
1.Механическая часть тягового подвижного состава : учеб. для вузов ж.-д. трансп. / И. В. Бирюков и др.; под ред. И. В. Бирюкова. – М. : Транс-
порт, 1992. – 440 с.
2.Минов Д. К. Механическая часть электрического подвижного состава. – М.-Л. : Госэнергоиздат, 1959. – 383 с.
3.Медель В. Б. Проектирование механической части электроподвижного состава. – М. : Транспорт, 1963. – 423 с.
4.Магистральные электровозы. Механическая часть электровозов / П. И. Аброскин и др. – М. : Машиностроение, 1967. – 435 с.
47
Учебное издание
Цихалевский Игорь Станиславович Нафиков Габдул-Ахат Маннанович Стаценко Константин Алексеевич
ВПИСЫВАНИЕ ТЕЛЕЖКИ ПОДВИЖНОГО СОСТАВА В КРИВУЮ
Методические рекомендации к выполнению расчетно-графической работы
по дисциплине «Основы механики подвижного состава» для студентов специальности 23.05.03 –
«Подвижной состав железных дорог» всех форм обучения
Редактор Н. А. Попова
Подписано в печать 09.10.2017. Формат 60х84 1/16. Усл. п. л. 2,8. Электронная версия. Заказ 255.
УрГУПС 620034, Екатеринбург, ул. Колмогорова, 66
48
