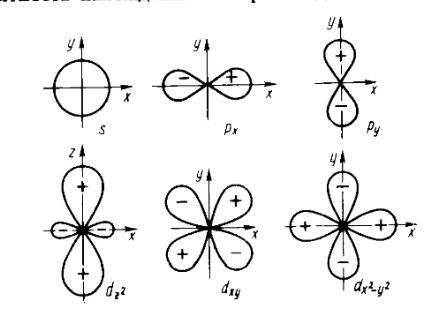
Угловая часть волновой функции

    При графическом представлении атомных орбиталей в виде

электронных облаков в пространстве вокруг ядра выделяются области, внутри которых преимущественно находится электрон (например, с вероятностью в 95%). Границы областей соответствуют определенным значениям угловой части волновой функции или ее квадрата. Поскольку характер симметрии электронных облаков при этом сохраняется, такое различие в больщинстве случаев несущественно. На отдельных частях изображений орбиталей часто указываются отвечающие им знаки волновой функции. 

Рис. 2.4. Диаграмма угловых частей волновой функции атома водорода

    Угловые части волновой функции определяют квантовые числа I и т

102

Функция г) называется радиальной 0 (0) — азимутальной, Ф (ф) — широтной. Обычно угловая часть волновой функции обозначается У = 0 (д) Ф (ф). Не приводя подробного решения уравнения 1.10 ,

рассмотрим лишь результаты определения радиальной и угловой частей волновой функции Ч .

    В котором / (г) называют радиальной частью, а К(0, ф) — угловой частью волновой функции.

103

    Угловые части волновой функции У[, для и р-атомных орбиталей представлены в табл. 1 в зависимости от значений квантовых чисел I и т. Здесь же приведены полные волновые функции полученные с учетом радиальных частей Я (г) для тех же АО. 

    В табл. 5 представлены волновые функции, соответствующие трем низшим энергетическим уровням атома водорода. Отметим, что произведение, содержащее угловую часть волновой функции,

умноженную на r , где I — азимутальное квантовое число, может быть записано в виде простого выражения в декартовых координатах. 

    К(0, <р) — угловая часть волновой функции 

    УСб, ф ) — угловая часть волновой функции 2 — атомный номер элемента 2 — статическая сумма 2 — число соударений 7о — фактор соударений 

    Произведение функций 0(0) и Ф(<)з) представляет собой

угловую часть волновой функции 

104

 V — оператор потенциальной энергии У1т(9, 9 —угловая часть волновой функции водородоподобного атома 2 — заряд ядра а, Р — спиновые волновые функции

    Произведение функций 0(9) и Ф(ср) представляет собой угловую часть волновой функции  [c.27]

Билет 16

1.​ Интерференция света. Кольца Ньютона. Вывод формулы для радиуса кольца.

Интерференция - наложение двух волн, приводящее к устойчивой картине колебаний. Давать интерференцию могут только когерентные волны. Когерентные волны - волны одного типа, обладающие одинаковой частотой. постоянной разностью фаз и одинаковой поляризацией. Также волны имеют и одинаковую длину.

Условия когерентности:

1.​ Постоянная разность фаз 2.​ Одинаковый период колебаний 3.​ Одинаковая природа волн

Кольца Ньютона представляет собой частный случай интерференции в тонких пленках. Они наблюдаются при отражении света от соприкасающихся друг параллельной толстой стеклянной пластины и плоско выпуклой линзы с большим радиусом кривизны. Роль тонкой пленки играет зазор между пластиной и линзой.

Картина интерференции состоит из чередующихся светлых и темных полос при монохроматическом свете.

В полихроматическом свете кольца окрашены.

105

Вывод формулы: оптическая разность хода между лучами, отраженными от верхней и нижней поверхностей зазора на произвольном расстоянии r от оси линзы, которой соответствует толщина зазора h:

По теореме Пифагора: Пренебрегая величиной h^2 получим:

106

минимумы. Из этих соотношений следует, что радиусы k этих колец светлых Ньютона r_k в отраженном свете определяется:

Радиусы темных колец в отраженном свете:

2. Люминесценция. Правило Стокса. Закон Вавилова.

Люминесценция – нетепловое свечение вещества, происходящее после поглощения им энергии возбуждения, длительность которого значительно превышает период световых колебаний

Период световых колебаний: t ≈ 10^(-15)c

Формула, характеризующая люминесценцию, может быть записана как

I=k ϕ,

Обозначения величин:

I- интенсивность излучения (Вт/м²),

k - коэффициент пропорциональности (1/м²), ϕ - плотность потока излучения (Вт/м²).

Значение постоянных для конкретного материала можно определить экспериментальным путем.

Для построения графиков зависимостей величин в случае люминесценции, необходимо провести эксперименты, измерить интенсивность излучения

107

при различных значениях плотности потока излучения и построить соответствующие графики. Таким образом, можно проанализировать зависимость между этими величинами и выявить закономерности, характерные для конкретного вещества или процесса люминесценции

Правило Стокса

108

109