Билет 12

1. Поляризованный свет. Поляроиды. Закон Малюса.

87

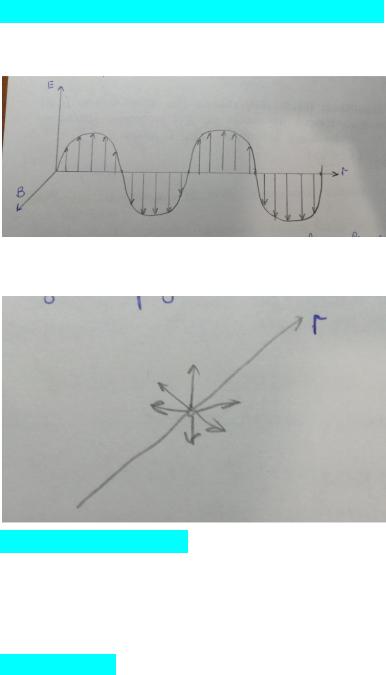
Свет - это поперечные волны, в которых E и B колеблются перпендикулярно направлению распространения волны. Далее будем рассматривать волну Е, именно она воспринимается глазами. Поляризованный ( плоскополяризованный) свет - свет, колебания Е которого происходят в одном и том же направлении, независимо от времени и независимо от расстояния, пройденного волной

Естественный свет - случай сочетания поляризованных волн ( колебания Е происходят в различных плоскостях)

Поляроид (поляризатор) - устройство, способное пропускать колебания Е только с направлением, изменяющимся по определенному закону. Представляет собой тонкую пленку. Изготавливают из вещества, обладающего свойством дихроизма - способностью неодинаково поглощать волны разной поляризации.

Закон Малюса - выражает зависимость интенсивности поляризованного света после его прохождения через поляризатор от угла (альфа) между плоскостями поляризации падающего света и поляризатора

88

Если поляризатор не идеальный, то на выходе получим частично поляризованный свет, который можно представить как:

Если на анализатор падает поляризованный свет интенсивностью I(0), а плоскость поляризации которого составляет угол (альфа) с плоскостью пропускания анализатора, то интенсивность пропущенного света I равна:

2. Дифракция электронов. Соотношение Гейзенберга. Волновая функция. Уравнение Шредингера Принципиальных отличий дифракции электронов от дифракции фотонов нет.

Условие дифракции - соизмеримость длины волны с расстоянием между рассеивающими центрами.

Впервые экспериментальное наблюдение дифракции было проведено Дэвисоном и Джермером: пучок электронов после рассеяния на кристалле Никеля дает дифракционную картину.

После них опыт провел Томсон: наблюдал дифракционную картину после прохождения пучка электронов через поликристаллическую золотую пластину.

Этот опыт повторялся и для настолько слабых пучков электрона, что через прибор могла проходить только одна частица. То есть волновые свойства присущи не только пучку электронов, но и каждому электрону в отдельности.

89

Закон де-Бройля: Соотношение неопределенностей Гейзенберга:

Каждая частица, обладающая волновыми свойствами имеет свой волновой пакет ( набор разрешенных длин волн)

Волновой пакет - определенная совокупность волн, обладающих разными частицами, которые описывают обладающую волновыми свойствами частицу, ограниченную во времени и пространстве.

В результате сложения результирующую волну с амплитудой, отличной от нуля, и занимающую ограниченную область пространства.

Принцип неопределенности - фундаментальное соображение, устанавливающее предел точности одновременного определения пары характеризующих систему квантовых наблюдаемых.

90

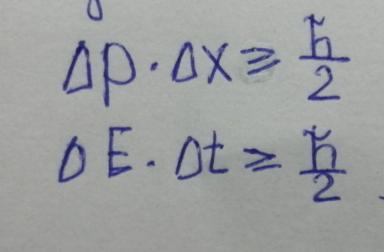- неопределенность Гейзенберга вследствие того, что объекты являются волнами

Волновая функция - математическое выражение, описывающее волну де Бройля. Не имеет физического смысла.

Имеет физический смысл квадрат модуля этой функции (квадрат амплитуды волны де Бройля равен плотности вероятности обнаружения микрообъекта в данной точке пространства)

Уравнение Шредингера имеет два вида:

1.Стационарное:

2.Временное:

Самое верхнее Уравнение временное, т.к. его решение представляет собой волновую функцию, зависящую от координат и времени.

91

Смысл уравнения Шредингера:

оно позволяет найти волновую функцию микрообъекта, если известны условия его движения.

Уравнение Шредингера - квантово - механический аналог второго закона Ньютона.

Основная задача квантовой механики - найти волновую функцию микрообъекта.

Стационарные задачи - в них условия движения микрообъекта не меняются со временем, т.е. U зависит только от координат.

Уравнение Шредингера предназначено для частиц без спина, движущихся со скоростями, много меньшими скорости света.

Уравнение позволяет найти волновую функцию микрообъекта, если известны условия его движения. Условия движения микрообъекта, подставляем U в уравнение и решаем. В нем появляется множество констант (они связаны с различными физическими величинами, описывающими движение) После получения волновой функции, предъявляем к ней требования. Затем видно, что величины дискретны

92