
Расчетно-графические работы по статистики
.pdf
Расчетно-графическая работа №1
Статистическое распределение выборки. Гистограмма. Точечные оценки.
Вариант 8
Задание 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Случайная выборка: |
|
|
|
Вариационный ряд: |
|
|
|
||||||||||||
81 |
73 |
75 |
68 |
74 |
83 |
71 |
72 |
72 |
72 |
61 |
64 |
65 |
66 |
67 |
67 |
67 |
67 |
68 |
68 |
69 |
76 |
67 |
77 |
65 |
74 |
64 |
95 |
71 |
67 |
68 |
69 |
70 |
70 |
70 |
71 |
71 |
71 |
71 |
72 |
80 |
70 |
68 |
85 |
77 |
77 |
84 |
72 |
70 |
71 |
72 |
72 |
72 |
72 |
72 |
73 |
73 |
74 |
74 |
75 |
79 |
70 |
72 |
81 |
81 |
68 |
66 |
75 |
75 |
61 |
75 |
75 |
75 |
76 |
77 |
77 |
77 |
79 |
79 |
80 |
73 |
72 |
71 |
81 |
85 |
75 |
81 |
67 |
67 |
79 |
81 |
81 |
81 |
81 |
81 |
83 |
84 |
85 |
85 |
95 |
Объем выборки: n=50;
Число интервалов группировки: k=7; Наименьшее значение варианты: m=61; Наибольшее значение варианты: M=95; Размах выборки: = − = 34 Интервал группировки: h= (95-61)/7 = 5
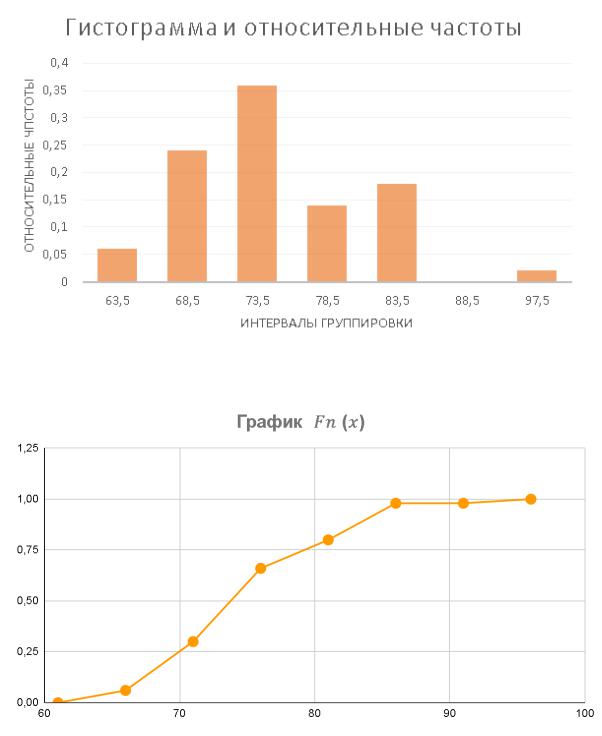
Выборочное среднее: x = 74,68
Выборочная дисперсия: s= 44,51795918 (s = 43,6276)
Выборочное среднеквадратическое отклонение: σ = 6, 67217799373
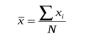
Ответы на вопросы:
1. Что такое генеральная совокупность?
Генеральная совокупность — совокупность всех объектов (единиц), относительно которых предполагается делать выводы при изучении конкретной задачи. Она состоит из всех объектов, которые имеют качества, свойства, интересующие исследователя.
2. Что называется выборкой объема n?
Выборкой объема n называется часть генеральной совокупности, которую случайным образом отбирают для наблюдения.
3. Что такое варианта?
Варианта — это отдельное значение варьируемого признака, которое он принимает в ряду распределения.
4. Как определяется вариационный ряд?
Вариационный ряд определяется путем упорядочивания значений признака в порядке возрастания или убывания. Это означает, что вы собираете все данные, относящиеся к изучаемому признаку, а затем располагаете их в последовательном порядке от наименьшего значения к наибольшему или наоборот.
5. Какой график называется гистограммой?
Гистограммой называется диаграмма с горизонтальным расположением оси категорий, в которой значения ряда данных определяют высоты последовательно расположенных вертикальных столбиков. При наличии в гистограмме нескольких рядов данных вертикальные столбики объединяются в группы, каждая из которых соответствует одной категории.
6. Что называется генеральным средним?
Генеральным средним называют среднее арифметическое всех значений генеральной совокупности. Если значения генеральной совокупности имеют соответствующие частоты, то формула для вычисления генеральной средней выглядит так:
xi — значения генеральной совокупности. n — объём генеральной совокупности.
7. Что называется генеральной дисперсией?
Генеральной дисперсией D называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения хi.

8. Что такое точечная оценка?
Точечная оценка – отдельное число (точка), которое используется в качестве оценки параметра генеральной совокупности. Точечной оценкой называют статистическую оценку, которая определяется одним числом *Q = f(x1, x2, …, xn), где x1, x2, …, xn ─ результаты n наблюдений над количественным признаком Х (выборка).
9. Какие оценки называются состоятельными и несмещенными?
Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру , то есть .
Смещенной называют статистическую оценку , математическое ожидание которой не равно оцениваемому параметру.
10.Каким образом определяется выборочное среднее?
Выборочное среднее определяется формулой:
11.Каким образом определяется выборочная дисперсия?
Выборочная дисперсия определяется формулой
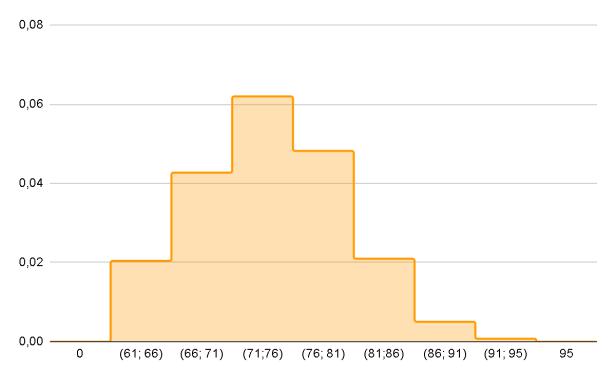
Расчетно-графическая работа №2
Статистическое распределение выборки. Гистограмма. Точечные оценки.
Вариант 8
Задание 2. μ=74; σ =6,31
i |
[hi-1,hi) |
zi |
Ф(zi) |
pi |
pi/h |
npi |
ni |
|
|
|
|
|
|
|
|
|
|
1 |
(-∞, 66) |
-∞ |
-0,5 |
0,102 |
0,0204 |
5,1 |
3 |
|
|
|
|||||||
-1,27 |
-0,398 |
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
[66, 71) |
-0,48 |
-0,1844 |
0,2136 |
0,04272 |
10,68 |
12 |
|
|
|
|
|
|
|
|
|
|
3 |
[71, 76) |
0,32 |
0,1255 |
0,3099 |
0,06198 |
15,495 |
18 |
|
|
|
|
|
|
|
|
|
|
4 |
[76, 81) |
1,11 |
0,3665 |
0,241 |
0,0482 |
12,05 |
7 |
|
|
|
|
|
|
|
|
|
|
5 |
[81, 86) |
1,90 |
0,4713 |
0,1048 |
0,02096 |
5,24 |
9 |
|
|
|
|
|
|
|
|
|
|
6 |
[86, 91) |
2,69 |
0,4964 |
0,0251 |
0,00502 |
1,255 |
0 |
|
|
|
|
|
|
|
|
|
|
7 |
[91; +∞) |
∞ |
0,5 |
0,0036 |
0,00072 |
0,18 |
1 |
|
|
|
|
|
|
|
|
|
Ответы на вопросы:
1. Какое распределение называется нормальным?
Нормальное распределение (распределение Гаусса) — это особый тип распределения, при котором большинство значений сосредоточено около среднего. Его также называют колоколообразным распределением, а его график — кривой Гаусса, или гауссианой.
2. Что означает термин статистическая оценка?
Статистической оценкой неизвестного параметра распределения называется функция от наблюдаемых случайных величин, которая позволяет вычислить приближённое значение этого параметра.
3. Приведите статистическую оценку генерального среднего.
Статистическая оценка генерального среднего — это выборочная средняя, которая представляет собой среднее арифметическое значений признака выборочной совокупности.
Выборочная средняя является несмещённой оценкой генеральной средней, то есть она эквивалентна истинному среднему в генеральной совокупности.
4. Приведите статистическую оценку генеральной дисперсии.
Генеральная дисперсия Вг есть среднее арифметическое отклонение квадратов разности признаков x1,x2,...xn генеральной совокупности X от их среднего значения x¯г.
Оценкой генеральной дисперсии является исправленная или выборочная несмещенная дисперсия. Чтобы вычислить исправленную дисперсию, умножим полученную ранее выборочную дисперсию на множитель nn−1
5. Что такое поправка Шеппарда?
В.Ф.Шеппард установил, что погрешность в расчете дисперсии, вызванная применением сгруппированных данных, составляет 1/12 квадрата величины интервала (T.e.i^2/12), как в сторону занижения, так и в сторону завышения величины дисперсии. Поправка Шеппарда должна применяться, если распределение близко к нормальному, относится к признаку с непрерывным характером вариации, построено по большому количеству исходных данных (n >500)
6. Поясните смысл правило «3сигм».
Правило 3 сигм означает, что вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю, то есть вероятность попадания очередного случайного значения в доверительный интервал с заданным значением три сигма близится к 100%
7. Что называют выравнивающими частотами?
Выравнивающими (теоретическими) частотами называют частоты, найденные теоретически.
Они вычисляются по формуле ni' = nPi, где n — число испытаний, а Рi — вероятность наблюдаемого значения хi, вычисленная при допущении, что величина имеет предполагаемое распределение. Они показывают, сколько в среднем элементов выборки должно попасть в i-й интервал
группировки
8. Что такое критерий согласия?
Критерий согласия — это статистическое правило, по которому принимается или отвергается статистическая гипотеза о том, что исследуемая случайная величина подчиняется заданному эмпирическому закону распределения, построенному на основе наблюдений, имеющихся в распоряжении исследователя.

Расчетно-графическая работа №3
Построение доверительного интервала
Вариант 8 Задание 3.
1. Построить доверительные интервалы с доверительными вероятностями равными 0.9, 0.95 и 0.99 по выборке объема 10 (малая выборка), отвечающей нормальной случайной величине. Изобразить полученные интервалы на общей числовой оси и сделать заключение о влиянии величины доверительной вероятности на ширину интервала.
Малая выборка: {69, 69, 84, 70, 68, 75, 74, 82, 85, 75}. 2). Построить доверительные интервалы с доверительными вероятностями равными 0.9, 0.95 и 0.99 по выборке объема 50 (из задания 1), отвечающей нормальной случайной величине. Изобразить полученные интервалы на общей числовой оси и сделать заключение о влиянии величины доверительной вероятности на ширину интервала
1. |
|
|
|
1 |
(69+ 69+ 84+70+ 68+75+ 74+ 82+85+ 75) = 75,2 |
|
|
|
|
|||
S |
= 101−1 |
|
|
|
|
|
|
|
|
|||
|
2 Х |
= |
|
|
((6910 |
-75,2)2+(69-75,2)2+(84-75,2)2+(70-75,2)2+(68-75,2)2+(75-75,2)2+(74-75,2)2+(82-75,2)2+(85-75,2)2+(75-75,2)2=41.8 |
|
|||||
|
|
|
|
|
|
|||||||
n=10 |
|
|
|
|
|
α |
zα .9 |
|
Доверительный |
|||
Х = 75,2 |
|
интервал |
||||||||||
|
|
|
||||||||||
|
|
|
377 |
|
|
|
|
|
||||
S2 = |
|
= 41.8; (S= 6,47216) |
|
|
|
|
||||||
|
0,9 |
1,83 |
75,2±3,745 |
(71,4; |
||||||||
|
|
|
|
9 |
|
|
|
|
|
78,9) |
||
|
|
|
|
|
|
|
|
|
0,95 |
2,262 |
75,2±4,629 |
(70,6 |
|
|
|
|
|
|
|
|
|
|
|
|
;79,8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,99 |
3,250 |
75,2±6,651 |
(68,5; |
|
|
|
|
|
|
|
|
|
|
|
|
81,8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД: Чем больше доверительная вероятность, тем больше доверительный интервал.
2. ВЫБОРКА: 61 64 65 66 67 67 67 67 68 68 |
n=50 |
|||||||||||||
68 69 70 70 70 71 |
71 71 71 |
72 |
X =61 |
|||||||||||
72 72 72 72 72 73 |
73 74 74 |
75 |
S2 = 213,92 |
|||||||||||
75 |
75 |
75 |
76 |
77 |
77 |
|
77 |
79 |
79 |
|
80 |
|
||
81 |
81 |
81 |
81 |
81 |
83 |
|
84 |
85 |
85 |
|
95 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
α |
|
zα .49 |
|
|
|
|
|
|
Доверительный |
|
||||
|
|
|
|
|
|
|
|
интервал |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||
0,9 |
|
1,64 |
|
61±3,39 |
|
(57,6 64,4) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
0,95 |
|
1,96 |
|
61±4,05 |
|
(56,9 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
;65,1) |
|
|
||
|
|
|
|
|
|
|
|
|
||||||
0,99 |
|
2,576 |
|
61±5,33 |
|
(55,7; |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
66,3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД: Чем больше доверительная вероятность, тем больше доверительный интервал.

Ответы на вопросы:
1. Что называется доверительным интервалом?
Доверительный интервал — это интервал, построенный по результатам наблюдений над случайной величиной, накрывающий с заданной вероятностью неизвестное значение параметра распределения этой случайной величины.
2. Что такое доверительная вероятность?
Доверительная вероятность — это вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал. Другими словами, это показатель точности измерений.
3. Как вычисляется исправленная выборочная дисперсия?
Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:
В данной формуле DГ – это истинное значение дисперсии генеральной совокупности. Исправить выборочную дисперсию можно путем умножения ее на дробь:
Получим формулу следующего вида:
Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2.
Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:
При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах.
4. Какой распределение называется распределением Стьюдента?
Распределение Стьюдента (t-распределение) — это однопараметрическое семейство абсолютно непрерывных распределений.
