ЛР№3н

ЛАБОРАТОРНА РОБОТА №3

ДОСЛІДЖЕННЯ СТІЙКОСТІ СИСТЕМИ АВТОМАТИЧНОГО УПРАВЛІННЯ ЗА КРИТЕРІЄМ МИХАЙЛОВА

МЕТА РОБОТИ: Оволодіти навиками дослідження стійкості системи за допомогою математичної системи MathCAD, засвоїти методи дослідження стійкості за критерієм Михайлова та впливу коефіцієнта передачі системи на її стійкість.

ТЕОРЕТИЧНІ ПОЛОЖЕННЯ

1. Стійкість. Стійкість – це здатність системи автоматичного керування повертатися у вихідний стан після зняття обмежених збурюючих або керуючих дій на систему. Основоположником вчення про стійкість є видатний академік А. М. Ляпунов. Він дав точне математичне визначення стійкості й розробив основні теоретичні положення, які лежать в основі сучасних методів дослідження стійкості.

Аналіз стійкості системи автоматичного управління нерозривно пов’язаний з дослідженням руху системи, який можна описати диференціальними рівняннями. Для визначення стійкості системи необхідно розв’язати диференціальне рівняння

С1,…,Сn — постійні інтегрування, які визначаються початковими умовами. Вид залежності (2) визначається коренями характеристичного рівняння.

Оскільки залежності в (2) являють собою експоненти, то для затухання перехідного процесу, а, значить, і стійкості системи необхідно, щоб дійсні

корені чи дійсні частини комплексних коренів були від'ємними.

Якщо хоча б один корінь характеристичного рівняння буде мати додатну дійсну частину, то загалом перехідний процес буде зростаючим, а система - нестійкою.

2. Критерій стійкості Михайлова. Далеко не завжди буває зручно і можливо обчислювати корені характеристичного рівняння. Тому були розроблені такі правила (критерії), за допомогою яких можна судити про стійкість системи безпосередньо без знаходження коренів. Ці правила називаються критеріями стійкості.

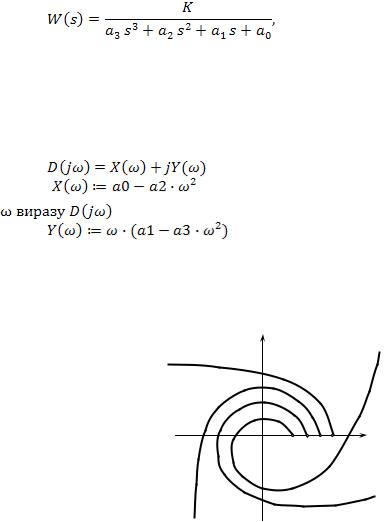
У 1931 р. А.В.Михайлов розробив графоаналітичний метод дослідження стійкості системи автоматичного регулювання. Визначення стійкості автоматичної системи за критерієм Михайлова проводиться на основі аналізу передаточної функції замкненої системи автоматичного управління у наступному порядку. Записують передаточну функцію замкненої системи:

Записують вираз для характеристичного поліному:

Виконують заміну комплексної змінної s на уявну змінну jω, розділяють вираз на дійсну Х(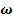) і уявну Y(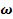) частини і отримують вираз для кривої Михайлова:

степені.

Змінюючи значення ω у межах 0≤ ω ≤∞ будують на комплексній площині криву Михайлова, рис.1.

Y

n=2

n=5

0 1=0 X

n=4

n=3

Рис. 1. Форма кривих Михайлова для стійких систем другого n=2, третього n=3 , четвертого n=4 та п’ятого n=5 порядків

Крива Михайлова для стійких систем повинна починатися на дійсній додатній осі і послідовно обходити n квадрантів площини проти ходу годинникової стрілки (рис. 1). Крива повинна мати плавну спіралеподібну форму, причому її кінець повинен прямувати до нескінченності у тому квадранті комплексної площини, номер якого дорівнює степені характеристичного рівняння n.

Для нестійкої системи така послідовність проходження квадрантів кривої Михайлова порушується.

2

ПОРЯДОК ВИКОНАННЯ РОБОТИ

1. Запустити програму MathCAD. Використовуючи кнопку Math, Vector and Matrix Toolbar, пункт (m..n), задати діапазон зміни частоти :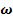

:=0,0.001..10

2. Задати коефіцієнти a3, a2, a1 згідно вказаного варіанту, обчислити і присвоїти відповідне значення коефіцієнту a0=Крац+1, де Крац - значення, отримане при виконанні лабораторної роботи №1, та формули для обчислення дійсної та уявної частини кривої Михайлова:

:=

:=

:= :=

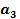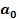3. За допомогою кнопок Math, Graph, X-Y Plot побудувати криву Михайлова стійкої системи. Задаємо для осі ординат Y(), для осі абсцис -

Х() так, як показано на рис. 2. Встановити масштаб осі Х(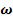) та осі Y()

відповідно до діапазону їх зміни.

При неповному, або частково неповному відображенні кривої Михайлова на графіку, необхідно змінити діапазон частот ω, заданий у п.1,

або масштаб осі Х() та осі Y() так, щоб найбільш повно відобразити криву.

Рис.2. Крива Михайлова стійкої системи третього порядку: n=3

3

За виглядом кривої Михайлова зробити висновок про стійкість

автоматичної системи згідно критерію Михайлова.

4. Збільшити коефіцієнт Крац до значення Кгр, отримане при виконанні лабораторної роботи №1, обчислити і присвоїти відповідне значення коефіцієнту a0 та побудувати криву Михайлова для системи на границі стійкості.

5. Збільшити коефіцієнт Крац до значення 1,3Кгр, отримане при виконанні лабораторної роботи №1, обчислити і присвоїти відповідне

значення коефіцієнту a0 та побудувати криву Михайлова нестійкої системи.

Оформлення звіту

Звіт має містити:

1.Назву і мету роботи.

2.Графіки кривих, отриманих при виконанні п. 3, 4, 5.

3.Висновки по роботі.

Контрольні питання

1.Яка залежність використовується для дослідження стійкості за критерієм Михайлова?

2.Сформулюйте критерій стійкості Михайлова.

3.Сформулюйте послідовність операцій для побудови кривої Михайлова.

4.Яку форму мають криві Михайлова для нестійкої системи та системи на границі стійкості?

Список літератури

1.Мартиненко И.И. и др. Автоматика и автоматизация производственных процессов. - М.: Агропромиздат, 1985.

2.Головінський Б.Л., Шуруб Ю.В., Лисенко В.П. Теорія автоматичного управління. -К.: ВЦ НУБіП України, 2012.-240 с.

3.Лисенко В.П., Головінський Б.Л., Руденський А.А., Шевченко М.М. Теорія автоматичного управління/навчальний посібник для студентів спеціальності АУТПВ. -К.: РВЦ НАУ, 2003.-109 с.

4.Зайцев Г.Ф., Костюк В.И., Чинаев П.И. Основы автоматического управления. - К.: Техніка, 1977.

5.Имаев Д.Х., Краснопрошина А.А., Яковлев В.Б. Теория автоматического управления. Ч.1. Линейные системы автоматического управления. - К.: Вища школа, 1992.

6.Кудрявцев Е.М. Mathcad 8. - М.: ДМК, 2000.

4