
ЛР1_К_РР
.pdf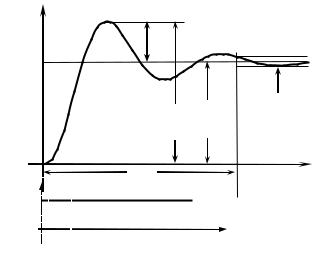
ЛАБОРАТОРНА РОБОТА №1
ДОСЛІДЖЕННЯ ПЕРЕХІДНОГО ПРОЦЕСУ ЛІНІЙНОЇ СИСТЕМИ АВТОМАТИЧНОГО УПРАВЛІННЯ
МЕТА РОБОТИ: Дослідити вплив коефіцієнта передачі системи та часу запізнення на характер перехідного процесу.
ТЕОРЕТИЧНІ ПОЛОЖЕННЯ
Динамічні властивості системи автоматичного управління описуються диференціальними рівняннями. У загальному випадку диференціальне рівняння лінійної системи з постійними коефіцієнтами за відсутності зовнішніх збурень має вигляд:
an |
d n y |
|
an 1 |
d n 1 y |
|
... a1 |
dy |
|
a0 y(t) |
|
(1) |
|||||
dt |
n |
|
dt |
n 1 |
dt |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
b |
d m x |
b |
|
d m 1 x |
... b |
|
dx |
b x(t) |
|
|
||||||
|
m |
|
|
|
m 1 |
|
|
|
|
|
||||||
m |
dt |
m 1 |
|
dt |
1 |
|
dt |
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
де y(t) – вихідна величина; |
|
x(t) |
– вхідна величина (управляюча дія); |
а0, |
||||||||||||
а1,…,аn і b0, b1,…,bm... постійні коефіцієнти; |
t – час. |
|
|
|||||||||||||
Розв’язок диференціального |
рівняння при заданих початкових умовах |
|||||||||||||||
і вхідній величині |
описує |
|
залежність |
|
вихідної |
величини системи |
від |
|||||||||
часу. Ця залежність визначає перехідний процес системи. При аналізі роботи системи використовують два типи залежностей вихідної величини від часу: перехідну функцію; імпульсну перехідну функцію.
Залежність вихідної величини системи від часу, яка визначається розв’язком диференціального рівняння при нульових початкових умовах і стрибкоподібній вхідній величині у вигляді функції 1(t) називається перехідною функцією. Перехідна функція позначається h(t).
Графік перехідної функції називається перехідною характеристикою. h(t)
σ
 2Δ
2Δ
|
max |
уcт |
|
y |
y |
0 |
tp |
t |
|
|
1(t)
1
0
Рис.1. Перехідна характеристика системиt автоматичного керування: x(t) = 1(t) – стрибкоподібна вхідна величина
Розв’язок диференціального рівняння при нульових початкових умовах і імпульсній вхідній величині у вигляді дельта–функції Дірака (t)
називається імпульсною перехідною функцією. Графік імпульсної перехідної функції називається імпульсною перехідною характеристикою.
За формою кривої перехідного процесу можна дати оцінку якості роботи системи автоматичного управління. Показники якості, які визначаються безпосередньо за кривими часових динамічних характеристик системи, називають прямими. Ці показники дають оцінку точності роботи автоматичної системи в перехідному (динамічні показники: час регулювання, перерегулювання, коливальність) і усталеному (усталене значення статичної похибки) режимах.
Величину максимальної динамічної похибки регулювання за час перехідного процесу характеризує перерегулювання . Перерегулювання визначається відношенням максимального відхилення вихідної величини від усталеного значення до усталеного значення, вираженим у процентах:
|
ymax y уст ) |
100% , |
(2) |
|
y уст
де ymax — максимальне значення, а yуст — усталене значення вихідної величини.
Перерегулювання характеризує перехідну складову похибки регулювання δn(t). Допустиме значення перерегулювання для тієї або іншої системи автоматичного керування визначається допустимими значеннями відхилень параметрів технологічних процесів. У більшості випадків вважається, що величина перерегулювання не повинна перевищувати 10— 30%. Однак у деяких випадках потрібно, щоб перехідний процес протікав узагалі без перерегулювання, тобто був монотонним, у деяких інших випадках може допускатися перерегулювання 50—70%.
Усталене значення вихідної величини yуст характеризує точність роботи автоматичної системи в усталеному режимі. Цю точність оцінюють вимушеною складовою похибкою регулювання δв(t), яка визначається як різниця між заданим x0(t) і усталеним yуст значеннями вихідної величини системи: δв(t)= x0(t)- yуст.
Узагальному випадку значення похибки δв(t) визначається як сума похибки відтворення завдання та похибки δf(t), обумовленої збурюючими діями при їх наявності: δз(t)= δв(t)+ δf(t).
Основна вимога, що ставиться до системи, полягає в тому, щоб відхилення керованої величини від завдання як в перехідному, так і в усталеному режимах роботи були якомога менші.
Усистемах, які реалізують принцип керування за відхиленням, вимушена (усталена) складова похибки, як відомо, може бути зменшена за рахунок збільшення коефіцієнта підсилення системи к. Проте зі збільшенням коефіцієнта к зменшується запас стійкості системи, зростає коливальність перехідного процесу, тобто збільшується перехідна складова похибки. Таким
2

чином, у системах з управлінням за відхиленням існує протиріччя між умовами підвищення точності в усталеному та перехідному режимах. Через це при виборі к доводиться приймати компромісне рішення, яке забезпечить допустиме значення усталеної похибки і задовільний перехідний процес.
Швидкодія системи характеризується за тривалістю перехідного процесу. Тривалість перехідного процесу оцінюють за часом регулювання
tрег. Час регулювання визначається проміжком |
часу від |
моменту |
надходження вхідного стрибкоподібного сигналу |
до того моменту, коли |
|
різниця між заданим і фактичним значеннями вихідної величини стає
меншою від |
деякої |
величини : y(t)- yуст ≤ . |
Величина |
являє собою |
||
зазвичай допустиму похибку і характеризує |
зону |
нечутливості |
регулятора. |
|||
Вона, як правило, |
становить 3-5% |
від |
заданого значення вихідної |
|||
величини. |
|
|
|
|
|
|
Число |
півперіодів коливань n |
за |
час перехідного |
процесу tрег |
||
називають коливальністю перехідного процесу. Коливальність для більшості систем автоматики становить звичайно 1…2. У деяких системах коливання можуть взагалі не допускатися, а іноді може допускатися до 3—4 коливань.
Перерегулювання і коливальність в основному залежать від запасу стійкості системи і можуть бути його опосередкованим показником. Чим
ближче знаходиться система |
до границі стійкості, тим більші |
значення |
мають і n. |
|
|
Показники якості, які |
безпосередньо визначаються за |
кривими |
перехідних процесів, широко використовуються не тільки при формуванні вимог до якості роботи автоматичних систем, теоретичних дослідженнях якості регулювання, але і при налагодженні, настроюванні та експлуатації систем з використанням експериментальних часових характеристик.
ПОРЯДОК ВИКОНАННЯ РОБОТИ
1.Запустити програму MATLAB.
2.Для створення моделі натиснути кнопки: бібліотеки Simulink  і у цьому середовищі
і у цьому середовищі  - створити файл.
- створити файл.
3.Скласти схему моделі автоматичної системи. рис.2. Для цього необхідно перемістити із бібліотеки Simulink у відкритий файл елементи, показані на рис.2 та описані у п.6.1-6.4.
4.З'єднання окремих блоків у схему здійснюється шляхом з'єднання виходів блоків помічених ">" із входами інших за допомогою лівої кнопки миші.
5.Для переходу у режим настройки необхідно навести курсор на відповідний блок і двічі натиснути на ліву кнопку миші.
3

 +-
+- 

 .
.
Scope
Рис.2. Схема моделі дослідження перехідних функцій
6.Призначення блоків та їх настройка.
6.1.Розділ Sources, блок Step – блок, який формує одиничний стрибкоподібний сигнал.
Налаштування блоку: Step time = 0, Initial value = 0, Final value = 1.
6.2.Розділ Continuous, блок Transfer Fcn – блок, який моделює передаточну функцію. Numerator – коефіцієнти чисельника передаточної функції. Denominator - коефіцієнти знаменника передаточної функції. У MatLab передаточна функція представляється у вигляді поліному:
W(s) |
b xn b |
xn 1 |
b |
|
xn 2 |
... b |
|
|||
n |
n 1 |
|
n 2 |
|
0 |
. |
(3) |
|||
a |
yn a |
n 1 |
yn 1 |
a |
n 2 |
yn 2 |
... a |
|||
|
n |
|
|
|
|
0 |
|
|
||
Передаточна функція системи задається шляхом введення відповідних значень коефіцієнтів чисельника bn та знаменника an, які заносяться у розділ Parameters послідовно і розділяються інтервалами.
Приклад:
Для передаточної W(s) |
|
|
30 |
|
e 12s |
коефіцієнти чисельника (k): b0 |
|
|
|
|
|
||||
15s |
2 |
5s 1 |
|||||
|
|
|
|||||
= 30, коефіцієнти знаменника: a2=15, a1=5, a0=1. Відповідні настройки блоку
“Transfer Fcn” у Matlab показані на рис.3.
a) |
b) |
|
|
Рис. 3. Блок “Transfer Fcn”: |
а – загальний вигляд; b - настройки блоку: |
||
чисельник b0 =К=30, Numerator [30];
знаменник a2=15, a1=5, a0=1, Denominator [15 5 1].
6.3. Розділ Continuous, блок Transport Delay – блок, який реалізує чисте запізнення Time delay.
4

Для прикладу, наведеного вище, налаштування блоку показано на
рис.4.
Рис. 4. Настройки блоку “Transport Delay” з часом чистого запізнення =12.
6.4. Розділ Sinks, блок Scope (осцилограф).
7. Настроювання параметру “Simulation” “Parameters”. Час моделювання, параметр Stop time, необхідно вибрати таким, щоб якісно та повністю відобразити перехідний процес (рис. 5).
Рис. 5. Настройки часу моделювання: t [0 … 100].
8. Запуск моделі здійснюється кнопкою “Start Simulation”, рис. 6.
Рис. 6. Кнопка “Start Simulation”
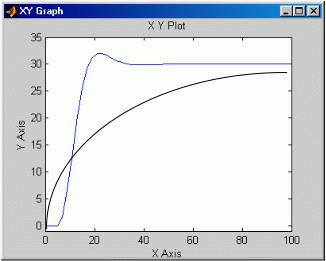
Для отримання графіку необхідно зробити мишею подвійний клік на зображенні осцилографа Scope на схемі. На екрані з’явиться вікно з графіком перехідної функції, рис. 7. Масштаб зображення встановлюється натиском на піктограму бінокля, рис.8.
5
1-Крац
2-Кап
Рис. 7. Графік перехідного процесу
ПРОГРАМА РОБОТИ
1.Ввести значення параметрів блоку Transfer Fcn відповідно до варіанту, заданого викладачем:
Numerator [b0], b0 - дорівнює номеру варіанту;
Denominator [а3 а2 а1 1].
Коефіцієнт а0=1 для всіх варіантів.
2.Ввести значення параметру Time delay блоку Transport Delay рівне
нулю.
3.Запустити процес моделювання, натиснувши на кнопку Start simulation, рис. 8.
4.Отримати зображення кривої перехідного процесу автоматичної системи без запізнення, зробивши мишею подвійний клік на зображенні осцилографа Scope і натиснувши на піктограму бінокля, рис. 7.
5.Дослідити характер перехідного процесу автоматичної системи без запізнення, змінюючи значення загального коефіцієнту передачі системи К в сторону зростання в орієнтовних межах від 0,1 до 50:
5.1.Визначити значення Кап і отримати графік перехідного процесу системи при аперіодичному русі, рис. 7, крива 2.
5.2.Визначити значення Крац, при якому значення перерегулювання знаходиться в межах 20-30%, і отримати графік перехідного процесу системи при коливальному русі, рис.7, крива 1.
5.3.Визначити значення Кгр і отримати графік перехідного процесу системи на границі стійкості, рис. 8.
6
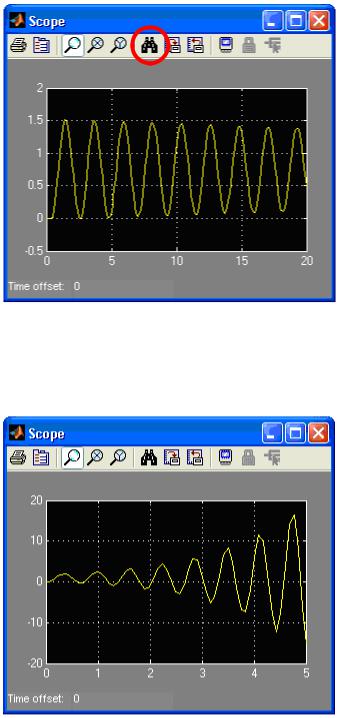
Рис. 8. Графік перехідного процесу системи на границі стійкості
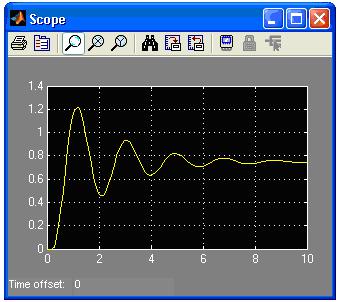
5.4. Вибрати значення К>Кгр і отримати графік перехідного процесу системи при нестійкому русі, рис.9.
Рис.9. Графік перехідного процесу нестійкої системи
6. Ввести значення параметру Time delay блоку Transport Delay згідно заданого варіанту, і дослідити характер перехідного процесу автоматичної системи із запізненням:
6.1. Встановити значення коефіцієнту передачі системи Крац і змінюючи значення чистого запізнювання в орієнтовних межах 0,01-1 (параметр Time delay блоку Transport Delay) отримати графік перехідного процесу системи на границі стійкості, рис. 8. Записати граничне значення запізнення τгран.
7
6.2. При коефіцієнті передачі системи Крац встановити значення чистого запізнювання τ<τгран/2 (параметр Time delay блоку Transport Delay) і отримати графік перехідного процесу системи з запізненням, рис. 10.
Рис. 10. Графік перехідного процесу системи з запізненням
ОФОРМЛЕННЯ ЗВІТУ
Звіт має містити:
1.Назву і мету лабораторної роботи.
2.Схему моделі.
3.Шість графіків перехідних процесів системи для пунктів 5, 6 програми.
4.Значення коефіцієнтів передачі системи Кап, Крац, Кгр, К>Кгр для п.5.1-
5.4програми та значення чистого запізнення τгран і τ<τгран/2 для п.6.1 і
6.2програми.
5.Висновки.
КОНТРОЛЬНІ ПИТАННЯ
1.Дайте визначення перехідної характеристики системи.
2.Дайте визначення імпульсної перехідної характеристики системи.
3.Назвіть основні типи перехідного процесу системи.
4.Як змінюється характер перехідного процесу системи при зміні коефіцієнта передачі?
5.Як впливає запізнення на перехідний процес системи?
СПИСОК ЛІТЕРАТУРИ
1.Мартиненко И.И. и др. Автоматика и автоматизация производственных процессов. - М.: Агропромиздат, 1985.
2.Головінський Б.Л., Шуруб Ю.В., Лисенко В.П. Теорія автоматичного управління. -К.: ВЦ НУБіП України, 2012.-240 с.
8
3.Лисенко В.П., Головінський Б.Л., Руденський А.А., Шевченко М.М. Теорія автоматичного управління/Навчальний посібник для студентів спеціальності АУТПВ. -К.: РВЦ НАУ, 2003.-109 с.
4.Зайцев Г.Ф., Костюк В.И., Чинаев П.И. Основы автоматического управления. - К.: Техніка, 1977.
5.Имаев Д.Х., Краснопрошина А.А., Яковлев В.Б. Теория автоматического управления. Ч.1. Линейные системы автоматического управления. - К.: Вища школа, 1992.
6.Дьяконов В. Matlab 6. Учебный курс. - Санкт-Петербург, Питер, 2001.
Табл.1. Варіанти завдань
Варіант |
а3 |
а2 |
а1 |
Варіант |
а3 |
а2 |
а1 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
8 |
16 |
3 |
6 |
10 |
|
|
|
|
|
|
|
|
2 |
3 |
4 |
7 |
17 |
4 |
5 |
11 |
|
|
|
|
|
|
|
|
3 |
4 |
5 |
6 |
18 |
5 |
4 |
12 |
|
|
|
|
|
|
|
|
4 |
5 |
6 |
5 |
19 |
6 |
3 |
13 |
|
|
|
|
|
|
|
|
5 |
6 |
7 |
4 |
20 |
7 |
2 |
14 |
|
|
|
|
|
|
|
|
6 |
7 |
8 |
6 |
21 |
8 |
3 |
15 |
|
|
|
|
|
|
|
|
7 |
8 |
9 |
10 |
22 |
9 |
4 |
14 |
|
|
|
|
|
|
|
|
8 |
7 |
10 |
11 |
23 |
8 |
5 |
13 |
|
|
|
|
|
|
|
|
9 |
6 |
11 |
12 |
24 |
7 |
6 |
12 |
|
|
|
|
|
|
|
|
10 |
5 |
12 |
13 |
25 |
6 |
7 |
11 |
|
|
|
|
|
|
|
|
11 |
4 |
11 |
14 |
26 |
5 |
8 |
10 |
|
|
|
|
|
|
|
|
12 |
3 |
10 |
12 |
27 |
4 |
9 |
8 |
|
|
|
|
|
|
|
|
13 |
2 |
9 |
11 |
28 |
3 |
10 |
7 |
|
|
|
|
|
|
|
|
14 |
1 |
8 |
10 |
29 |
2 |
11 |
6 |
|
|
|
|
|
|
|
|
15 |
2 |
7 |
9 |
30 |
4 |
12 |
5 |
|
|
|
|
|
|
|
|
9
