
Курсова Скудря ТОА-1
.pdf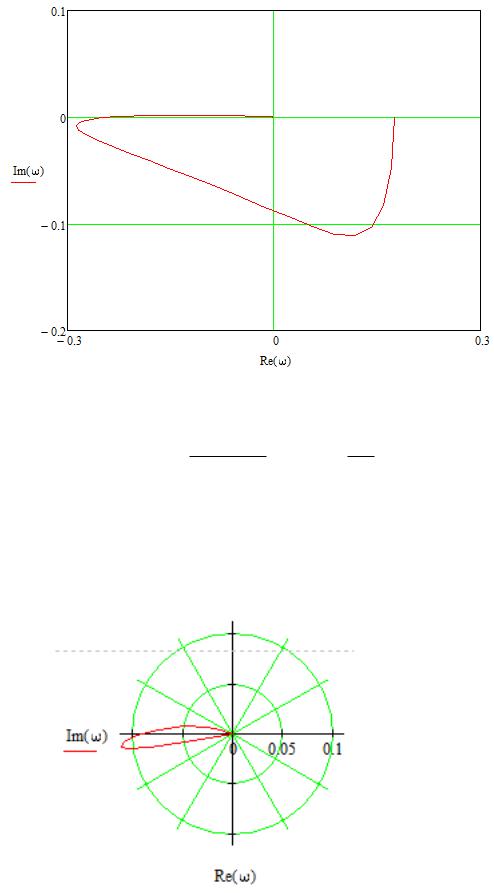
Рис. 7.1. Годограф Найквіста (червона лінія)
або |
∆ =− 20 |
1 |
=− 20 |
1 |
= 13, 979 |
|
| (0.025 )| |
0.2 |
Для визначення запасу стійкості системи за фазою φ необхідно на рис.
7.2 нарисувати коло одиничного радіусу з центром на початку координат (чорна пунктирна лінія).
Рис. 7.2. Визначення запасу стійкості за фазою
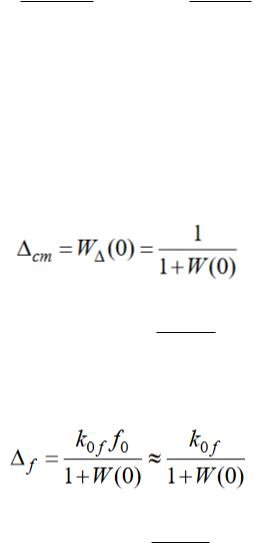
8 ОЦІНКА ЯКОСТІ РЕГУЛЮВАННЯ
Якість роботи системи автоматичного регулювання оцінюється за стійкістю, показниками якості перехідного процесу, точністю в усталеному режимі. До основних показників якості перехідного процесу відносяться: час регулювання, перерегулювання, коливальність процесу.
Дослідження стійкості системи проведено при виконанні п.7. Запаси стійкості за модулем і фазою складають:
Δφ = 80 град.
Основні показники якості регулювання були визначені у розділі 6: - час регулювання tp = 385 c;
-перерегулювання % =
-коливаня N = 1.
− (∞) |
* 100% = |
0.76−0.6 |
(∞) |
0.6 |
Точність автоматичної системи прийнято оцінювати за значенням похибки в статичному режимі й усталеному динамічному режимі.
Статична похибка в усталеному режимі визначається передаточною функцією замкнутої системи відносно похибки (5.4) при р=0:
Для досліджуваної САР отримуємо |
∆ст |
= |
1 |
= 0, 368 |
|
1+1,714 |
Складова статичної похибки від збурюючої дії розраховується за формулою:
Для досліджуваної САР отримуємо |
∆ |
= |
0.01 |
= 0. 003 |
|
1+1.714 |

9 СЕРЕДНЄ КВАДРАТИЧНЕ ВІДХИЛЕННЯ ВИХІДНОЇ ВЕЛИЧИНИ ПРИ ДІЇ НА СИСТЕМУ ВИПАДКОВОГО ЗБУРЕННЯ
1 = 1 ( 0 Тд Тв)2 = 0,17 (0,17 30 50)2 = 11 050
2 = − 1 ( 0 (Тд + Тв))2 = −0,17 (0,17 (30 + 50))2 = −31.443
3 = 1 ( 0 )2 = 0,17 (0,17)2 = 0.004913
0 = Тд Тв Т = 30 50 200 = 300000 = 3,0 105
1 = Т Тд + Т Тв + Тв Тд = 200 30 + 200 50 + 50 30 = 17
500
2 = Тд + Тв + Т = 30 + 50 + 200 = 280
3 = 1 + з = 1 + 4.05 = 5.05
10 ВИСНОВКИ
Система автоматичного регулювання є стійкою. Загальний коефіцієнт передачі системи складає 4.05. Запас стійкості за фазою ∆ = 80°. Час регулювання системи 385 секунд. Коливальність 1. Система є точною, похибка в усталеному режимі 0,3. Середньоквадратичне
відхилення вихідного сигналу при дії випадкового збурення на систему 2 =
1. 59∙10−5. Оскільки запаси стійкості та перерегулювання відповідають вимогам завдання, можна зробити висновок, що розроблена САР відповідає вимогам завдання на курсову роботу.
