

|
Критерії стійкості Михайлова |
|
План |
1 |
Критерій стійкості Михайлова |
2 |
Криві Михайлова стійкої системи |
3 |
Криві Михайлова нестійкої системи |
4 |
Дослідження стійкості за критерієм Михайлова |

КРИТЕРІЙ СТІЙКОСТІ МИХАЙЛОВА
•У 1931 р. А.В.Михайлов розробив графоаналітичний метод дослідження стійкості системи автоматичного регулювання. Визначення стійкості проводиться на основі аналізу характеристичного рівняння.
•Розглянемо окремо ліву частину характеристичного рівняння, яка являє собою характеристичний поліном:
M(r) a0rn a1rn 1 ... an 1r an
•Виконаємо заміну змінної r на уявну змінну jω:
M ( j ) a0 ( j )n a1 ( j )n 1 ... an 1( j ) an

КРИТЕРІЙ СТІЙКОСТІ МИХАЙЛОВА
• Наведемо характеристичний поліном у вигляді вектора:
M ( ) Re( ) j Im( )
• де дійсна частина містить парні степені :
Re( ) an an 2 2 ...
• а уявна — непарні степені : |
|
3 |
|
|
Im( ) a |
a |
... |
||
n 1 |
n 3 |
|
||
•Визначаючи значення Re( ) і Im( ) вектора за цими формулами при різних значеннях від 0 до можна побудувати графік функції M(j ) на комплексній площині - криву Михайлова.

Критерій стійкості Михайлова
•Для стійких систем крива Михайлова повинна починатись
на дійсній додатній осі (при =0 Re(0)=аn і Im(0)=0), послідовно обходити n квадрантів площини проти годинникової стрілки. Крива повинна мати плавну спіралеподібну форму, а в n-му квадранті комплексної площини її кінець повинен прямувати до нескінченності, де n - номер квадранта, який дорівнює степені характеристичного рівняння.
•Для нестійкої системи послідовність проходження квадрантів кривої Михайлова порушується

Криві Михайлова стійкої системи
Im
n=2
n=5
0 |
1=0 |
Re |
|
|
n=4 |
n=3
Форма кривих Михайлова для стійких систем другого
n=2, третього n=3 , четвертого n=4 та п’ятого n=5 порядків
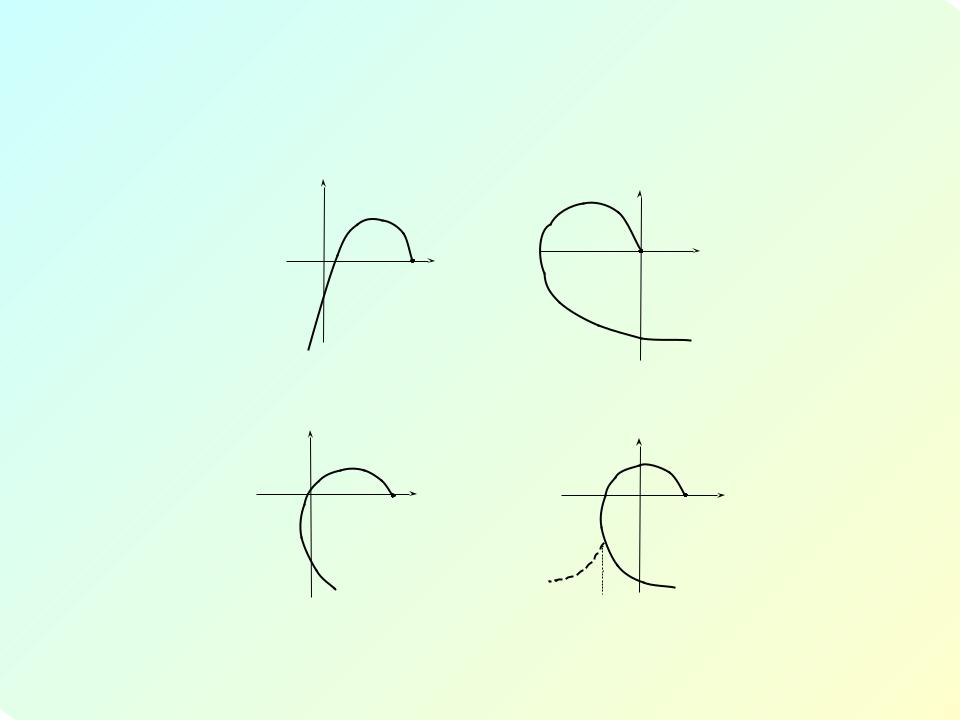
Криві Михайлова нестійкої системи (а), та системи на границі стійкості (б, в, г).
|
Y |
|
|
Y |
|
|
|
|
|
|
|
|
X |
X |
|
|
|
0 |
|
0 |
|
=0 |
|
|
|
|
|
||
n=3 |
|
|
|
n=4 |
|
|
|
|
а |
|
б |
|
Y |
|
Y |
n=4 |
|
|
||
0 |
|
X |
X |
0 |
=0 |
|
|
0 |
=0 |
||
n=4 |
|
a0<0 |
a0>0 |
|
|
||
|
|
a0=0 |
|
в |
г |

ПРИКЛАД
•Дослідити стійкість системи, якщо характеристичне рівняння має вигляд:
2r3 3r2 5r 1 0.
•Для системи 3 порядку характеристичний поліном запишеться:
M( j ) a3 ( j )3 a2 ( j )2 a1 ( j ) a0 ,
•де дійсна частина:
Re( ) aо а |
2 2 , |
• і уявна частина: |
|
Im( ) a1 a3 3.
Таблиця значень
•Підставивши значення коефіцієнтів поліному отримаємо:
Re( ) 1 3 2 .
Im( ) 5 2 3.
• Складемо таблицю значень для різних ω:
|
|
|
|
ω |
0 |
1 |
2 |
Rе(ω) |
1 |
-2 |
-11 |
Im(ω) |
0 |
3 |
-6 |
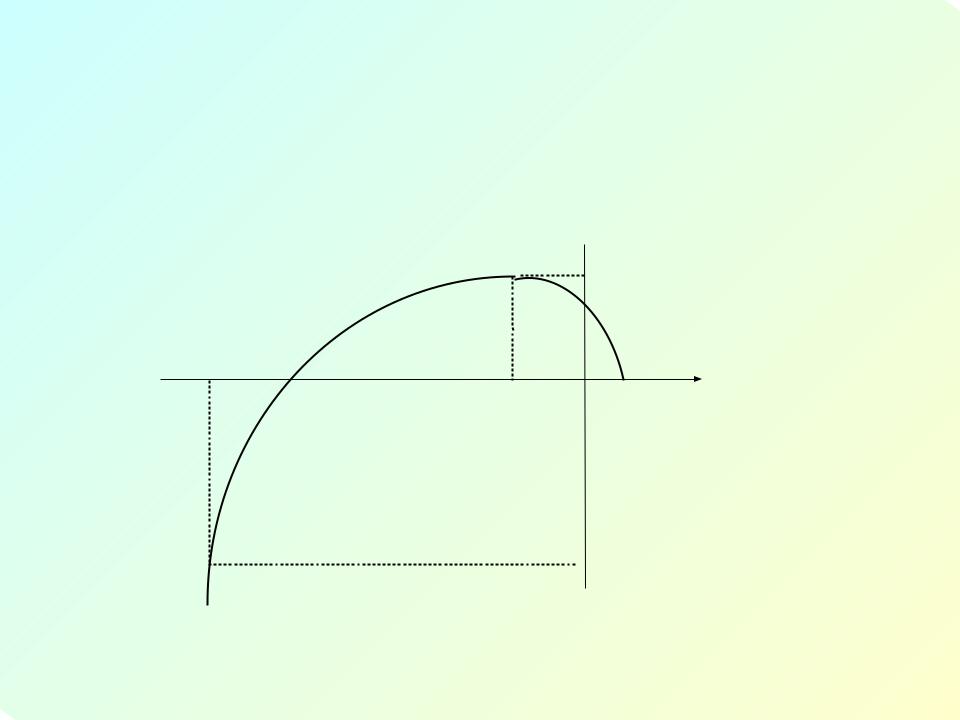
Крива Михайлова
•За таблицею значень будуємо криву Михайлова:
Im( )
3
-11 |
-2 |
0 |
1 Re( ) |
-6

Висновок
•Крива Михайлова починається на дійсній додатній осі (при =0 Re( )=1, а Im( )=0), послідовно обходить 3 квадранти комплексної площини проти годинникової стрілки, і в 3-му квадранті площини її кінець прямує до мінус нескінченності. Система є стійкою.
