ТОА ЛАБ 9 123123123
.pdf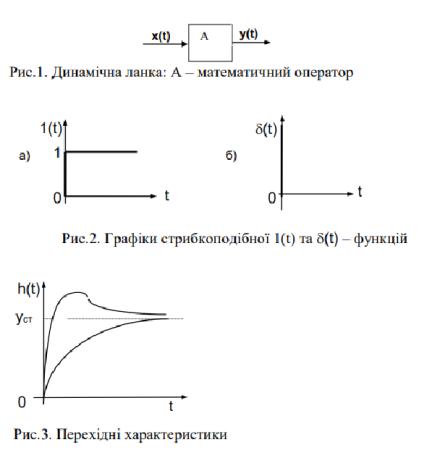
ЛАБОРАТОРНА РОБОТА №9
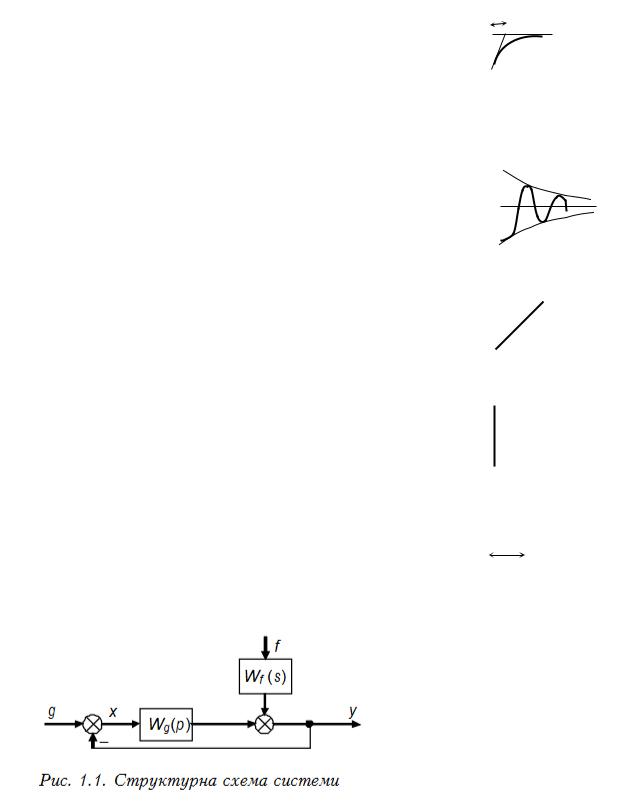
ДОСЛІДЖЕННЯ ПЕРЕХІДНИХ ХАРАКТЕРИСТИК ТИПОВИХ ДИНАМІЧНИХ ЛАНОК
МЕТА РОБОТИ: Дослідити та вивчити часові динамічні характеристики типових елементів автоматичних систем.
ТЕОРЕТИЧНІ ПОЛОЖЕННЯ
Теорія автоматичного управління при дослідженні систем використовує математичні моделі.
Математична модель системи автоматичного управління або елемента системи може бути подана в різних формах: диференціальних, різницевих, інтегральних чи алгебраїчних рівнянь, що описують стан системи. В залежності від виду руху системи розрізняють клас лінійних та нелінійних,
детермінованих та стохастичних, стаціонарних і нестаціонарних моделей. Найбільш простим є клас неперервних лінійних детермінованих моделей. Таким моделям відповідають звичайні лінійні
диференціальні рівняння з постійними коефіцієнтами n-го порядку:

a |
|
d n y |
a |
|
d n 1 y |
... a |
|
dy |
a |
|
y b |
|
d m x |
b |
|
d m 1x |
... b |
|
dx |
b |
|
x (1.1) |
|
0 dt n |
1 dt n 1 |
n 1 dt |
n |
0 dt m |
1 dt m 1 |
m 1 dt |
m |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
Диференціальне рівняння можна записати в операторній формі:
Q(p)y(t)=P(p)x(t),
де p=d/dt-оператор диференціювання, Q(p), P(p) - операторні поліноми степенів n та m. Диференціальні рівняння доповнюються початковими умовами.
Для дослідження власного руху системи при нульових початкових умовах використовується передаточна функція.
W(s)= |
Y(s) |
|
P(s) |
, |
(1.2) |
|
X(s) |
Q(s) |
|||||
|
|
|
|
де:Y(s), X(s) - зображення за Лапласом змінних y(t), x(t);
P(s), Q(s) - поліноми комплексного аргументу s степенів n і m.
Знаючи передаточну функцію і зображення вхідної змінної елемента чи
системи, легко знайти зображення вихідної змінної: |
|
Y(s)=W(s)X(s). |
(1.3) |
З усіх форм подання моделей вибирається найбільш зручна для дослідження системи.
Системи автоматичного управління та їх елементи часто моделюються типовими ланками. Найбільш часто використовуються такі типи ланок: пропорційна (безінерційна), інтегруююча, диференціююча, аперіодична першого порядку (інерційна), коливальна, запізнююча (чистого запізнювання).
2. Вивчити рівняння та перехідні функції типових динамічних ланок, наведених у табл.1 методичних вказівок до роботи.
|
Рівняння ланки |
|
Перехідна |
||
Назва ланки |
Передаточна функція |
|
|||
|
характеристика |
||||
|
Перехідна функція |
|
|||
|
|
|
|
|
|
1. Безінерційна |
y(t)=kx; |
h |
|
|
|
W(s) k ; |
|
|
|
||
|
|
|
|||
(підсилювальна, |
k |
|
|
|
|
h(t)=k1(t). |
|
|
|
||
пропорційна) |
0 |
|
|
|
|
|
t |
||||
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Інерційна |
Tdy / dt y kx ; |
|
h |
|
|
|
T |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(аперіодична |
W(s) k /(Ts 1) ; |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
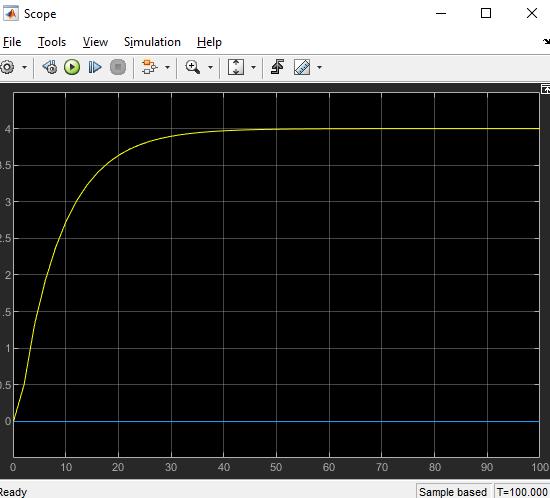
першого порядку) |
h(t) |
k(1 e |
t / T |
)1(t) . |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T 2d 2 y / dt 2 2 T dy / dt y kx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 ; |
|
h |
|
|
|
|
|
|
|
|
|
|||||||||
3. |
Коливальна |
W s |
|
|
2 |
2 |
|
k |
; |
|
|
|
|
|
|
|
|||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
T |
|
s |
2 Ts 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
h(t) k[1 e |
t |
( |
|
sin 1t |
cos 1t)]1(t) |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
t |
|||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y k xdt ; |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. |
Інтегруюча |
|
W(s) k / s ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
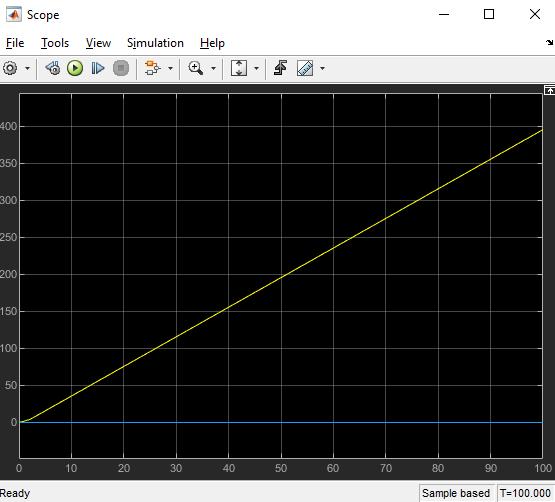
(астатична) |
|
h(t) kt 1(t) . |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y kdx / dt ; |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5. Диференціююча |
|
W(s) ks ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
h(t) k (t) . |
|
|
|
|
= k (t) |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x(t ) ; |
|
|
|
h |
|
|
|
|
|
1-(t- ) |
|
|
|
|
|
|
||||||||
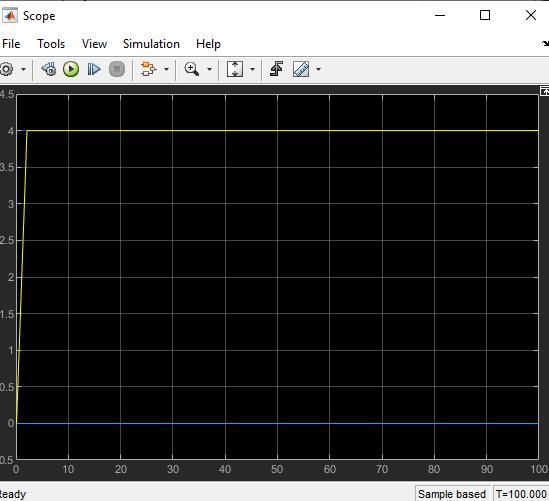
6. Чистого |
|
W(s) e s ; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
запізнювання |
|
h(t) 1(t ) . |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
t |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
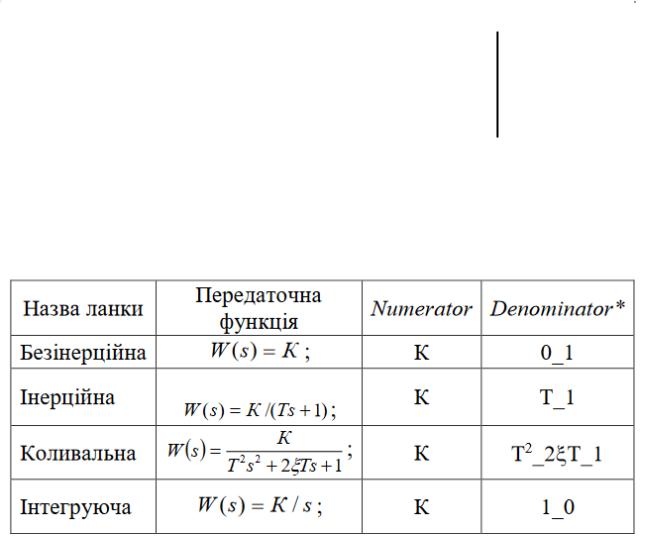
3 Записати у табл.1 передаточні і перехідні функції всіх елементарних ланок
|
Формули для |
Назва ланки |
Передаточної функції |
|
Перехідної функції |
1. Безінерційна |
W(s)=k; |
(підсилювальна, |
|
пропорційна) |
h(t)=k1(t). |
|
|
2. |
Інерційна |
Tdy / dt y kx ; |
|
W(s) k /(Ts 1) ; |
|||
(аперіодична першого |
|||
порядку) |
h(t) k(1 e t / T )1(t) . |
||
|
|
|
|
3. |
Інтегруюча |
y k xdt ; |
|
W(s) k / s ; |
|||
(астатична) |
|||
|
|||
|
|
h(t) kt 1(t) . |
|
|
|
|
|
|
|
y kdx / dt ; |
|
4. |
Диференціююча |
W(s) ks ; |
|
|
|
h(t) k (t) . |
|
|
|
|
|
|
|
y x(t ) ; |
|
5. |
Чистого |
W(s) e s ; |
|
запізнювання |
|||
|
|||
|
|
h(t) 1(t ) . |
|
|
|
|
|
Перехідна характеристика
h |
|
0 |
t |
|
h
= k (t)
0
t
4. Виконати аналітичні розрахунки перехідних функцій за формулами, наведеними в
табл.1. Підставте значення коефіцієнтів згідно зданих викладачем варіантом, табл.2 методичних вказівок, і прорахуйте кілька значень перехідної функції у граничних (t=0 та t, що прямує до нескінченності) та характерних (t=1, t=Т, t=3Т) точках.
Рівняння має вигляд:

1) Передавальна функція ОУ у загальному випадку може бути представлена у вигляді відношення:
де R(p) і Q(p) – зображення по Лапласу вихідний та вхідний змінних ОУ, що відповідають лівій та правій частинам рівняння. Звідси, передатна функція матиме вигляд:
2) Визначимо частотні показники ОУ. Відомо, що частотна передатна функція W(iφ) може бути представлена у вигляді: W(iω) = A(ω)eiφ(ω) = U(φ) + iV(φ)
де A(ω) – амплітудна частотна характеристика (АЧХ); φ(ω) – фазова частотна характеристика (ФЧХ);
U(ω) – речова частотна характеристика (ВЧХ); V(ω) – уявна частотна характеристика; Підставимо iω у вираз замість p. Отримаємо:
Виділимо окремо амплітудну та фазову частотні характеристики та підставимо чисельні значення коефіцієнтів. Виходячи з того що:
φ(ω) = arg(W(iω))
Для наших даних:
остаточно отримаємо:
Визначимо логарифмічну амплітудну частотну характеристику (ЛАЧХ). Відомо, що ЛАЧХ визначається із співвідношення:
L(ω) = 20lg(A(ω))
Ця характеристика має розмірність дБ (децибели) і свідчить про зміну відношення потужностей вихідний величини до вхідний. Для зручності ЛАЧХ будують у логарифмічному масштабі (рисунок 1).
Фазова частотна характеристика, побудована в логарифмічному масштабі, називатиметься логарифмічною фазовою частотною характеристикою (ЛФЧХ).
Визначимо імпульсну перехідну (вагову) функцію. Вагова функція w(t) є реакцією системи на одиничну імпульсну функцію, подану на її вхід. Вагова функція пов'язана з передатною функцією перетворення Лапласа.
W(p) = ∞∫0w(t)e-pt
Отже, вагову функцію можна визначити, застосувавши зворотне перетворення Лапласа до передавальної функції.
w(t) = L-1[W(p)]
Обчислимо приблизно коріння поліномів R(p) і Q(p), та був знайдемо зворотне перетворення Лапласа від передавальної функції і побудуємо графік вагової функції (рисунок 2).
Для обчислень представимо функцію у вигляді:

Вагова функція є похідною від перехідної функції h(t), яка є реакцією системи на ступінчасту дію.
Проінтегрувавши w(t) або виконавши зворотне перетворення Лапласа над W(p)/p, знайдемо перехідну функцію h(t) і збудуємо відповідний графік.
h(t) = 0.
5. За отриманими даними побудуйте криві перехідного процесу для всіх елементарних ланок. Отримані результати занести в табл.1.
|
Формули для |
|
|
Назва ланки |
Передаточної функції |
Перехідна |
|
характеристика |
|||
|
|
||
|
Перехідної функції |
|
|
1. Безінерційна |
W(s)=k; |
|
|
(підсилювальна, |
|
|
|
пропорційна) |
h(t)=k1(t). |
|
2. Інерційна |
Tdy / dt y kx ; |
|
|
|
W(s) k /(Ts 1) ; |
|
|
|
|
(аперіодична першого |
|
|
|
|
порядку) |
h(t) k(1 e t / T )1(t) . |
|
|
|
|
|
|
|
|
3. Інтегруюча |
y k xdt ; |
|
|
|
W(s) k / s ; |
|
|
|
|
(астатична) |
|
|
|
|
|
|
|
|
|
|
h(t) kt 1(t) . |
|
|
|
|
|
|
|
|
|
y kdx / dt ; |
h |
|
|
|
|
|
||
4. Диференціююча |
W(s) ks ; |
|
|
|
|
h(t) k (t) . |
0 |
|
|
|
t |
|||
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|||
|
|
||||
|
y x(t ) ; |
|
|
|
|
5. Чистого запізнювання |
W(s) e s ; |
= |
k (t) |
||
|
h(t) 1(t ) . |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
t |
||
|
|
|
|
|
|
6Запустити програму MatLab та провести дослідження перехідних характеристик
динамічних ланок згідно «Порядок розрахунку перехідних характеристик в середовищі MatLab, наведеного у методичних вказівках до роботи.
7.Побудувати графіки цих характеристик. Порівняти їх з графіками, отриманими шляхом аналітичних розрахунків.