Практика 9

Практика 9

ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

В прямоугольной декартовой системе координат Oxyz уравнение вто-

рого порядка может быть приведено к одному из следующих канонических

уравнений и определяет поверхность второго порядка или вырожденную

поверхность.

1

Последние три уравнения определяют вырожденные поверхности.

Цилиндрические поверхности состоят из параллельных прямых (обра-

зующих), пересекающих некоторую линию (направляющую). Если в уравне-

нии поверхности отсутствует переменная z, то уравнение определяет цилин-

дрическую поверхность с образующей, параллельной Oz, и направляющей с

F(x,y) 0,

уравнениями

z const.

Для построения не цилиндрических поверхностей второго порядка, как правило, применяется метод сечений.

x2 y2 1 и определяет эллипс (рис.47) с полуося- 9 4

ми 3 и 2, центром O 0;0;0 .

Сечения поверхности плоскостями Oxz и Oyz

Рис. 47

центр O 0;0;0 .

2

Рис. 49

3

деляет цилиндрическую поверхность с образующей, параллельной оси Oz. На-

правляющая в любой плоскости

z const имеет уравнение x2 y2 1 и

является гиперболой (рис.50).

Рис. 50

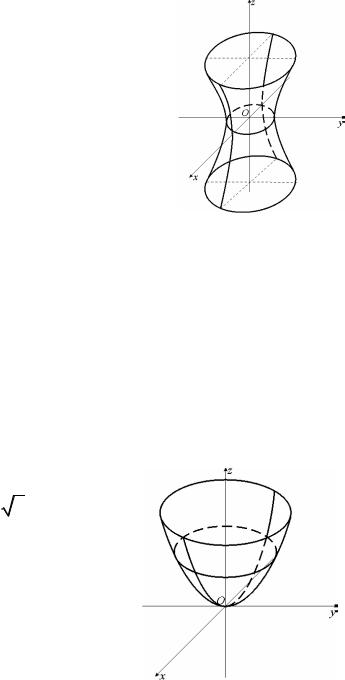
Пример 2.

Составить уравнение проекции на плоскость Oyz сечения эллиптиче-

ского параболоида y2 z2 x плоскостью x 2y z 0.

Решение.

Линия пересечения поверхности y2 z2 x плоскостью x 2y z 0

определяется системой y2 z2 x, x 2y z 0.

Для отыскания проекции этой линии на плоскость Oyz исключим x из

этой системы. Выразим x из каждого уравнения x y2 z2, x 2y z.

4

2). Найти центр и радиус окружности, являющейся сечением сферы

x 3 2 y 2 2 z 1 2 100 плоскостью 2x 2y z 9 0.

Указание. Центр окружности – проекция центра сферы на плоскость

сечения.

Ответ: 1;2;3 , R 8.

3). Определить, по каким линиям пересекаются поверхности

5