Добавил:

Engels Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

Дополнительные главы математики

Файл:

Практика 8

..pdf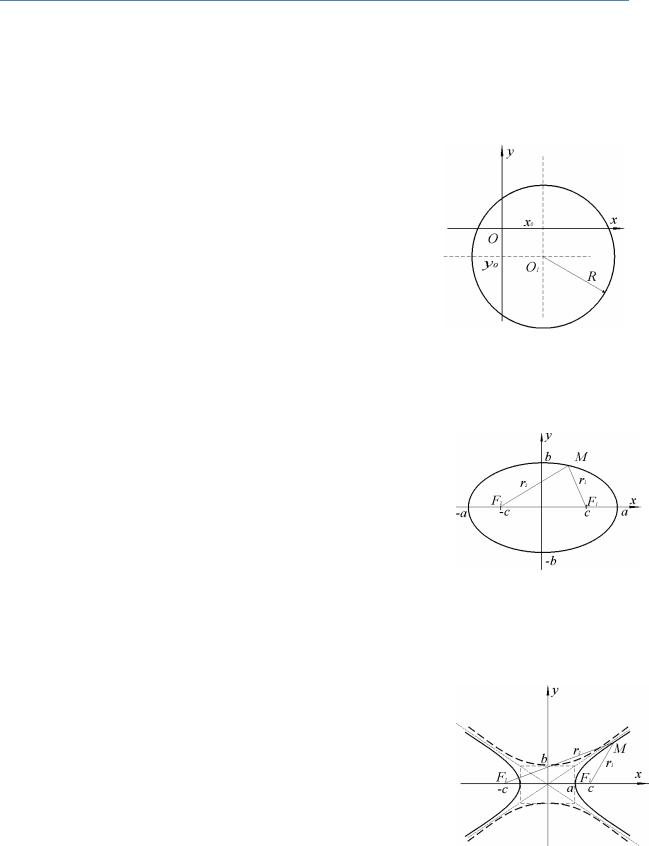

Скачиваний:

Добавлен:

13.07.2025

Размер:

554.21 Кб

Скачать

☆

Практика 8

КРИВЫЕ ВТОРОГОПОРЯДКА

Окружность (рис.33) – множество всех точек плоскости, равноудалён-

ных от данной точки (центра). Уравнение окружности с центром

O1 x0;y0 радиуса R:

x x0 2 y y0 2 R2.

Эллипс (рис.34)– множество всех точек
плоскости, сумма расстояний от которых до
двух данных точек (фокусов) есть величина
постоянная (обозначаемая 2a), большая, чем
расстояние между фокусами.				Рис.33
Каноническое уравнение эллипса:
	x2	y2	1,
	a2	b2

F1 c;0 , F2 c;0 – фокусы, a и b – большая и

малая полуоси эллипса,			2a 2c,				b2 a2 c2.
Уравнение эллипса с центром, смещенным в
точку O1 x0;y0 , и		осями,			параллельными осям
координат:
	x x	2		y y		0	2
	0							1.
	a2			b2

Гипербола (рис.35) – множество всех точек плос-

кости, модуль разности расстояний которых до двух данных точек (фокусов) есть величина по-

стоянная (обозначаемая 2a), меньшая, чем рас-

стояние между фокусами.

Каноническое уравнение гиперболы:

Рис. 34

Рис. 35

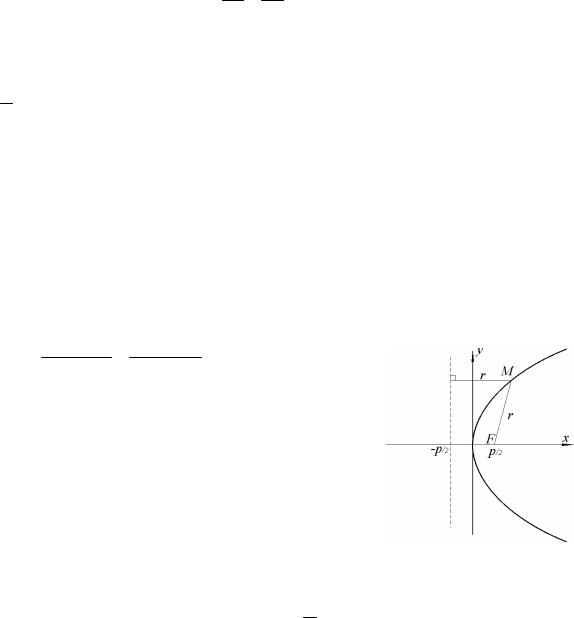
x2 y2 1, a2 b2

a, b– полуоси гиперболы, 2a 2c, b2 c2 a2, F1 c;0 , F2 c;0 – фокусы,

y b x – асимптоты. a

Сопряженные гиперболы

	x2		y	2				x	2	y	2
					1	и						1.
	a	2	b	2	1	и		a	2	b	2	1.
	a		b					a		b
(основная линия на рисунке)							(пунктир на рисунке)

Уравнение гиперболы с центром, смещенным в точку O1 x0;y0 парал-

лельно осям координат

x x0 2 y y0 2 1.

a2 b2

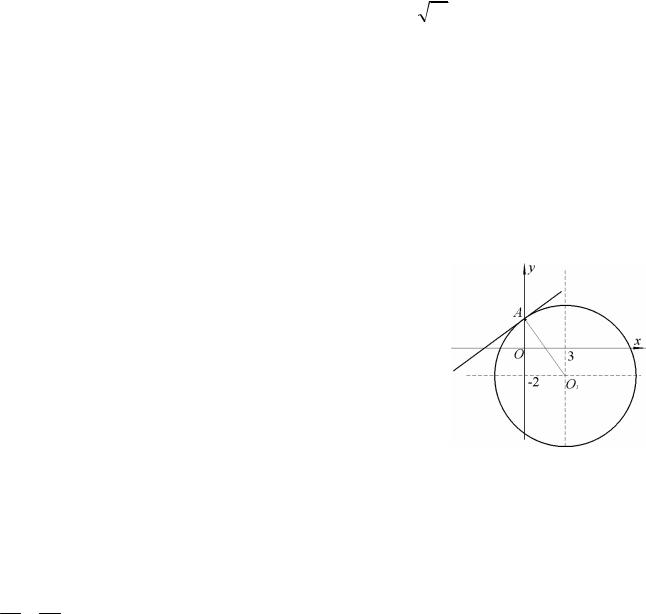
Парабола (рис.36) – множество всех то-

чек плоскости, равноудалённых от данной

точки (фокуса) и данной прямой (дирек-

трисы).

Каноническое уравнение параболы:

y2 2px,

ось симметрии совпадает с осью Ox, x p

Рис. 36

– директриса, F	p	;0	– фокус.
	2

Уравнение x2 2py	задает параболу,			ось симметрии которой совпадает с
осью Oy, директриса		p			p
	y		, фокус F	0;
		2
					2
Уравнение параболы с вершиной,					смещенной в точку O1 x0;y0 , и
осью симметрии, параллельной оси Ox:

y y0 2 2p x x0 .

Пример 1.

Составить уравнение окружности, проходящей через точки A 5;0 и

B 1;4 , если её центр лежит на прямой x y 3 0.

Решение.

Уравнение окружности со смещенным центром содержит три парамет-

ра x0, y0, R. Для их определения составим систему из трёх уравнений:

x	0	y		3 0,							(центр окружности на прямой x y 3 0),
	0	0	2		0 y			2		R2,
5 x			2		0 y		0	2		R2,	(точка A на окружности),
		0					0
				2	4 y				2	2
										R ,	(точка B на окружности).
1 x						0				R ,	(точка B на окружности).
		0				0

Результат решения системы: x0 2, y0 1, R 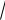10.

Таким образом, уравнение имеет вид: x 2 2 y 1 2 10.

Пример 2.

Составить уравнение касательной к окружности проведенной в точке A 0;2 .

Решение.

Воспользуемся уравнением прямой, проходя-

щей через заданную точку с заданным нормальным

вектором. Касательная, проходящая			через	точку
A 0;2 ,	имеет	нормальный	вектор
N1 O1A 0 3;2 2 3;4 . Таким образом, урав-
нение	касательной	3 x 0 4 y 2 0,		или

3x 4y 8 0.

x 3 2 y 2 2 25,

Рис.37

Пример 3.

Найти длину перпендикуляра, восстановленного из фокуса эллипса

x2 y2 1 к большой оси до пересечения с эллипсом. 9 4

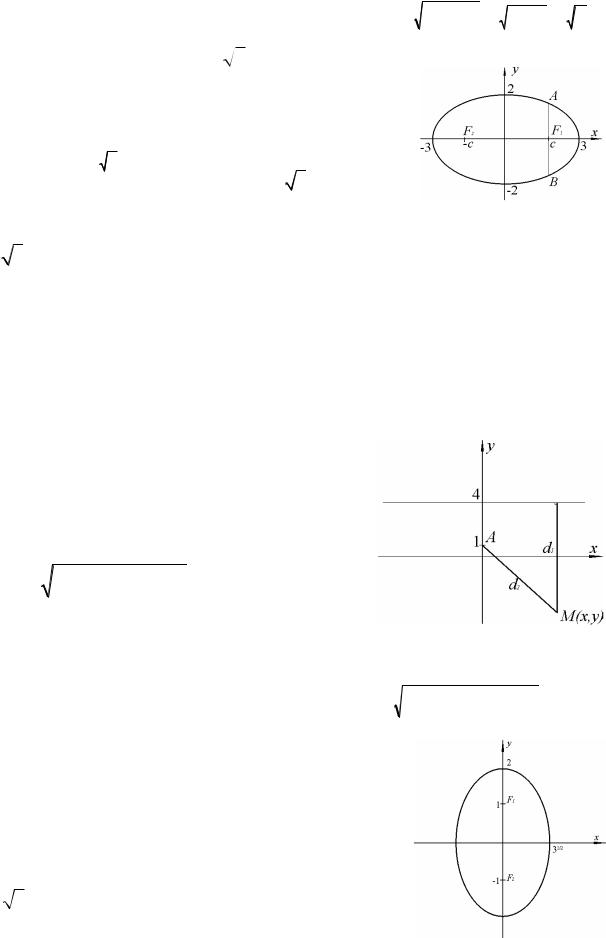
Решение.
	c; 0 ,		c; 0 , где
Фокусы эллипса F		F		c	a2 b2			.
Фокусы эллипса F		F		c	a2 b2	9 4	5	.
1		2

Уравнение перпендикуляра: x 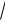5. Координа-

ты точек A и B пересечения эллипса и пер-

пендикуляра к большой оси удовлетворяют

			x			5,									4


системе:			x	2			y	2		откуда A				5;		,
системе:			x	2			y	2	1,	откуда A				5;	3	,

						4
			9			4										Рис. 38
		4							4		4	8				Рис. 38


B	5;		и		AB								.
B	5;	3	и		AB				3		3	3	.
		3							3		3	3

Пример 4.

Составить уравнение множества точек, расстояние которых от точки

A 0;1 в два раза меньше расстояния до прямой у 4 0.

Решение.

Пусть

M x;y – произвольная

точка

(рис.39). Расстояние от M до прямой y 4 0:

y 4

Расстояние от точки

M до точки

A: d2 x 0 2 y 1 2 .

По условию точка M x;y

принадлежит

Рис. 39

указанному в условии множеству тогда и толь-

ко

тогда,

когда d1 2d2 , откуда

y 4

x 0 2 y 1 2 , или

Таким образом, искомое множество точек – эллипс с центром в начале координат, оси которого совпадают с осями координат (рис.40). Полуоси

a 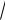3, b 2.

Рис. 40

Пример 5.

Асимптоты гиперболы имеют уравнения: y x. Составить уравнение

гиперболы, если она проходит через точку M 3;2 .

Решение.

Из уравнения асимптот получаем, что центр гиперболы находится в

начале координат и b 1, или a b. Тогда каноническое уравнение гипербо- a


лы принимает вид:				x2			y2		1.	Точка M					принадлежит гиперболе,
				x2			y2						3;	2
				a2			a2						3;	2
				a2			a2
			2					2
следовательно:		3	2			2		2		a	2
следовательно:	a2				a2				1,		2	1.
	a2				a2				1,			1.

Таким образом, искомое уравнение гиперболы x2 y2 1.

Пример 6.

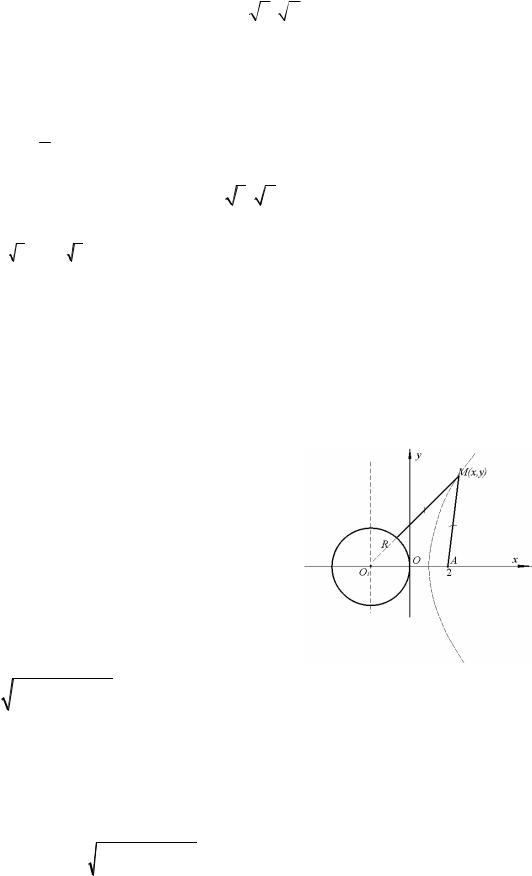
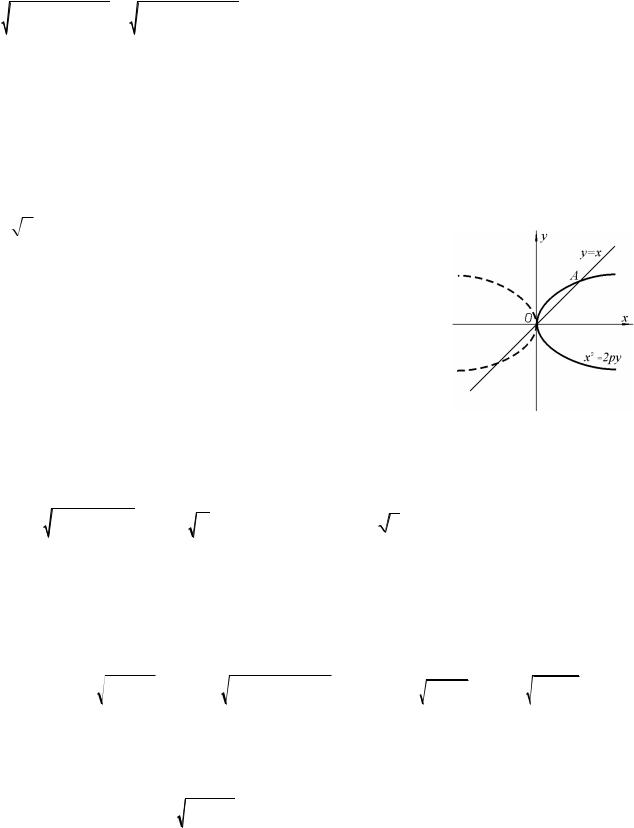
Найти уравнение множества точек, равноотстоящих от окружности

x2 4x y2

0 и от точки A 2;0 .

Решение.

Пусть

M x;y

–

произвольная

точка,

причем

x 0, иначе расстояние от точки

M до

окружности меньше расстояния от нее до точки

Расстояние

от

точки M x;y

до

точки

Рис. 41

A 2;0 :

x 2 2 y2 .

Расстояние от точки M до окружности: d MO1 R, где O1 x0;y0 –

центр,

R –

радиус окружности. Преобразуем уравнение окружности к виду

x 2 2

4, откуда x

2, y

R 2. Расстояние от точки M x;y

до точки O

2;0 : MO

x 2 2

y2 . Точка M принадлежит указанному

множеству					только		при			выполнении равенства:					MA d , или
												2		y2
												2		y2
	x 2	2	y	2		x 2	2	y	2	2, откуда получаем	x				1,	Получили
		2		2			2		2		x			3	1,
														3
													x 0.
													x 0.

правую ветвь гиперболы.

Пример 7.

Составить уравнение параболы с вершиной в начале координат, сим-

метричной относительно оси Ox и отсекающей от прямой y x отрезок

42.

Решение.

Вершина параболы – точка O 0;0 , Ox –

ось симметрии, следовательно, уравнение па-

раболы имеет вид y2 2px.

y x,

определяет координа-

Система

2px

Рис.42

ты точек пересечения прямой и параболы: O 0;0

A 2p;2p . Тогда

4p2 4p2 2

. По условию OA 4

, поэтому

Условию задачи удовлетворяют параболы y2 4x

и y2 4x.

Пример 8.

Установить тип линии, заданной уравнением, и построить линию:

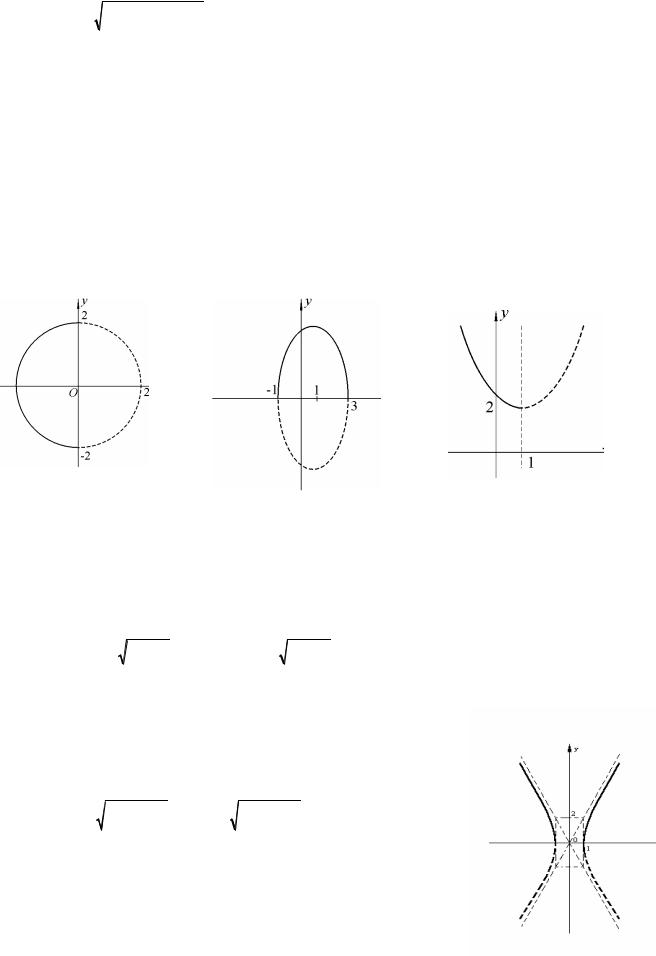
1) x 4 y2 ; 2) y 12 4x2 8x ; 3) x 1 y 2; 4) y 4x2 4.

Решение.

1). Преобразуем уравнение:

		x2 4 y2	x2 y2 4
x 4 y	2			.
		x 0	x 0.

Получили левую полуокружность с центром O 0;0 и радиусом R 2 (рис.43).

12 4x2 8x

y2 4x2 8x 12

2).

y 12 4x

y 0

y 0.

Выделим полный квадрат относительно

4 x 1 2

16,

y 0.

x 1 2

Разделим уравнение на 16: 16

y 0.

Получили верхнюю половину эллипса с центром 1; 0

и полуосями

a 2,

b 4 (рис.44).

Рис. 43

Рис. 45

Рис. 44

x 1 2

y 2

y 2 x 1 2

3).

x 1 y 2 x 1 y 2

x 1 0

x 1.

Эти соотношения определяют левую ветвь па-

раболы с вершиной 1;2 и осью симметрии,

параллельной оси ординат (рис.45).

4).

y 4x2 4 y 4x2 4

y2 4x2 4

4x2 y2 4

4 1,

y 0

y 0.

Рис. 46

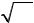
Эти соотношения определяют верхнюю половину гиперболы с центром

0;0 и полуосями a 1,b 2 (рис. 46).

Примеры для самостоятельного решения

1). Составить уравнение окружности, описанной около треугольника, сто-

роны которого заданы уравнениями 9x 2y 41 0, 7x 4y 7 0,

x 3y 1 0.

Указание. Определить координаты вершин треугольника и подставить их в уравнение окружности.

Ответ: x 3,1 2 y 2,3 2 22,1.

2). Составить уравнение общей хорды окружностей x2 y2 16 и

x 5 2 y2 9.

Ответ: x 3,2.

3). Определить координаты центров и радиусы окружностей:

1) x2 y2 8x 4y 0; 2) x2 5x y2 3y							1	0;
1) x2 y2 8x 4y 0; 2) x2 5x y2 3y								0;
						2
3) x2 y2 4x 14y 54 0.
Указание. Выделить полные квадраты по переменным x и y.
Ответ: 1) 4; 2 , R		5		3
		5		3
	20; 2)		;		, R 3; 3) R2	1 – уравнение не
	20; 2)	2	;		, R 3; 3) R2	1 – уравнение не
		2		2
имеет смысла (мнимая окружность).
4). Составить уравнение эллипса с фокусами F1 0;0						и F2 1;1 и длиной
большой полуоси a 1.
Указание. Воспользоваться определением эллипса.

Ответ: 3x2 3y2 2xy 2x 2y 1 0.

5). Найти центр и полуоси эллипса, заданного уравнением:

1) 5x2 9y2 30x 18y 9 0; 2)16x2 25y2 32x 100y 284 0 .

	Ответ: 1) 3; 1 , a 3, b 5; 2)					1;2 ,				a 5, b 4.
6).	Составить уравнение гиперболы,					проходящей через точку M 9;8 , если
асимптоты гиперболы имеют уравнения y									2				x.
									2		2
										3
										3
	Ответ:	x2	y	2	1.
	Ответ:	9	8		1.
		9	8
7).	Составить уравнение гиперболы, если она проходит через точку 2; 0 ,
а ее фокусы совпадают с фокусами эллипса							x	2				y		2	1.
а ее фокусы совпадают с фокусами эллипса							25				9				1.
							25				9
	Ответ:	x2	y	2	1.
	Ответ:	4	12		1.
		4	12