
Практика 6
..pdf
Практика 6
ПРЯМАЯ В ПРОСТРАНСТВЕ
Прямая в декартовой прямоугольной системе координат Oxyz может быть задана уравнением одного из следующих видов:
Ax B y C z D 0, |
|||
Общие уравнения: 1 |
1 |
1 |
1 |
A2x B2y C2z D2 0. |
|||
Прямая задана как линия пересечения двух плоскостей, где коэффици- |
|||
енты A1,B1,C1 не пропорциональны A2,B2,C2 . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 pt, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qt, |
|
где |
|
|
M |
|
x ;y |
|
;z |
|
|
– заданная |
|||||||||||||||||
Параметрические уравнения: y y |
0 |
|
|
|
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z0 rt, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
точка прямой, |
l p;q;r |
– направляющий вектор прямой. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Канонические уравнения прямой, проходящей через точку |
|
M0 x0;y0;z0 |
|||||||||||||||||||||||||||||||||||||||||||||||||
параллельно вектору l p;q;r : |
|
x x0 |
|
|
y y0 |
|
|
|
z z0 |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|||||||||
Уравнение прямой, |
проходящей через две заданные точки M1 x1;y1;z1 |
и |
|||||||||||||||||||||||||||||||||||||||||||||||||
M |
|
x ;y |
;z |
|
: |
x x1 |
|
y y1 |
|
z z1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2 |
2 2 |
|
2 |
|
|
y |
2 |
y |
|
z |
2 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Угол между прямыми с направляющими векторами l1 |
|
p1,q1,r1 |
и |
||||||||||||||||||||||||||||||||||||||||||||||
l2 p2,q2,r2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 l2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
cos cos l ,l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
l1 |
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Условие параллельности прямых: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
l |
l |
, или |
|
p1 |
|
|
q1 |
|
r1 |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
p2 |
|
|
q2 |
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Условие перпендикулярности прямых:
1
l1 l2 , или |
|
l1 l2 |
p1 p2 q1q2 r1r2 0. |
|
|
|
||||||||||||||
Расстояние от точки M |
1 |
x ,y ,z |
|
до прямой |
x x0 |
|
y y0 |
|
z z0 |
: |
||||||||||
|
|
|
||||||||||||||||||
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
p |
|
q |
|
r |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
M |
0 |
M |
1 |
, l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
d |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
Пример 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x y 3z 1 0, |
||||
Привести уравнения прямой к каноническому виду: |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x 4y z 7 0. |
||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 способ. Нормальные |
|
векторы |
|
плоскостей |
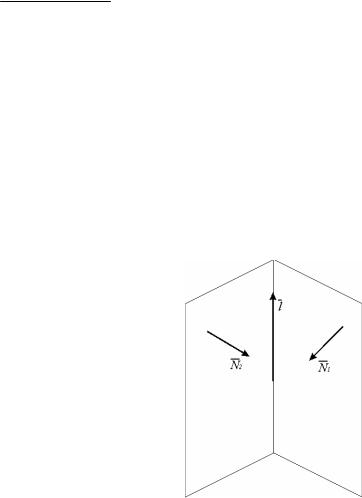
2x y 3z 1 0 и |
|||||||||||||||
5x 4y z 7 0 N1 2; 1;3 и N2 5;4; 1
соответственно. Эти векторы перпендикулярны
направляющему вектору l прямой. Поэтому
|
|
|
|
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
||
l N1 N2 |
2 |
1 |
3 |
11i 17j 13k . |
|
|||||||||||||||
|
|
|
|
5 |
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В качестве точки M0 x0,y0,z0 , через ко- |
|
||||||||||||||||||
торую проходит искомая прямая, можно взять, |
|
|||||||||||||||||||
например, |
точку её пересечения с координат- |
Рис.18 |
||||||||||||||||||
ной плоскостью Оху: |
z0 0, |
2x |
y |
|
|
1 0, |
|
|||||||||||||
|
0 |
|
0 |
|
|
откуда x0 11/13, y0 9/13, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5x0 4y0 7 0, |
|
||||||||
M0 11/13,9/13,0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Зная |
точку |
M0 |
и |
направляющий |
вектор |
l , запишем канонические |
|||||||||||||
|
|
|
|
|
|
x 11/13 |
|
y 9/13 |
|
z 0 |
|
|||||||||
уравнения прямой: |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||
|
11 |
|
|
|
17 |
|
|
13 |
|
|||||||||||
2

2 способ. Исключив из системы уравнений сначала y, потом x, получим
|
|
|
|
13x 11z 11 0, |
Разрешим каждое |
уравнение относительно z: |
||||||||||||||||||||||||||||||||
систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
13y 17z 9 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
13 |
x 11/13 |
|
|
13 y 9/13 |
|
|
|
|
x 11/13 |
|
|
|
y 9/13 |
z |
|
|||||||||||||||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, или |
|
|
|
|
|
|
|
|
|
|
. |
|
||||||
|
|
11 |
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
11 |
|
17 |
|
13 |
|
||||||||||||||||
|
|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Определить, при каком усло- |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
вии прямые |
|
x x1 |
|
|
y y1 |
|
z z1 |
|
и |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
q |
1 |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x x2 |
|
y y2 |
|
z z2 |
|
|
компланар- |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
q |
2 |
|
|
|
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ны, т.е. лежат в одной плоскости. |
|
|
|
|
|
|
|
|
|
|
Рис. 19 |
|
||||||||||||||||||||||||||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Данные прямые находятся в одной плоскости только при условии, что |
|||||||||||||||||||||||||||||||||||
векторы M1M2 x2 x1,y2 y1,z2 |
z1 , l1 p1;q1;r1 |
и l2 p2;q2;r2 |
ком- |
|||||||||||||||||||||||||||||||||||
планарны, |
|
т.е. смешанное |
произведение |
этих векторов равно |
нулю: |
|||||||||||||||||||||||||||||||||
M1M2, l1, l2 0 , или |
|
x2 x1 |
|
y2 y1 |
z2 z1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
p1 |
|
|
q1 |
r1 |
|
0 . |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
q2 |
r2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
Пример 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
В уравнениях прямой |
x |
|
y |
|
z |
определить параметр а так, чтобы эта |
|||||||||||||||||||||||||||||
|
|
|
|
3 |
a |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
прямая пересекаласьспрямой x 1 y 5 z , и найти точку их пересечения. 3 2 1
3
Решение. |
|
|
|
|
|
Направляющие векторы прямых l1 2, 3, a |
и l2 3,2,1 не являют- |
||||
ся коллинеарными, так как |
2 |
|
3 |
. Следовательно, эти прямые не будут па- |
|
|
|
||||
3 |
2 |
|
|
||
раллельными при любом значении а.
Запишем условие компланарности прямых (см. пример 2):
|
1 0 |
5 0 |
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
а |
0, откуда а 1. |
|
|
|
|
|
|
|
|
|||||||
|
3 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Координаты точки |
M0 x0,y0,z0 |
пересечения прямых есть решение |
|||||||||||||||||
|
|
|
|
x |
|
|
|
y |
|
z |
0 |
|
|
|
|
|
|||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
3 |
|
1 |
|
|
|
|
|
|||
системы, составленной из уравнений этих прямых: |
|
|
|
y |
|
|
z |
|
|
||||||||||
|
|
|
|
|
x |
|
1 |
5 |
0 |
|
|||||||||
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
, |
|||
|
|
|
|
|
|
3 |
|
|
|
2 |
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из первого равенства выразим x0 2z0, y0 3z0 |
и подставим во вто- |
||||||||||||||||||
рое, в результате получим x0 2, y0 |
3, z0 1, или M0 2, 3,1 . |
|
|
|
|||||||||||||||
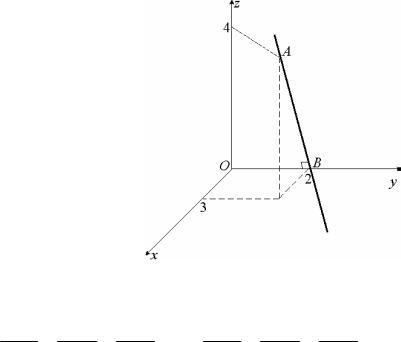
Пример 4.
Составить уравнения прямой,
проходящей через точку A 3;2;4 и пе-
ресекающей ось Oy под прямым углом.
Решение.
Искомая прямая перпендикулярна оси Oy и пересекает её, следовательно,
проходит через точку B 0;2;0 (рис.20).
Составим уравнение прямой, проходя-
щей через две заданные точки x 3 y 2 z 4, или
0 3 |
2 2 |
0 4 |
Рис.20
x 3 y 2 z 4.
3 0 4
4

Пример 5.
Выяснить взаимное расположение прямых x y 1 z 2 и 2 0 1
x 1 y 1 z 2. Вычислить угол между ними.
1 2 1
Решение.
Проверим условие компланарности, т.е. лежат ли прямые в одной
|
1 0 |
1 1 |
2 2 |
|
плоскости (см. пример 2): |
2 |
0 |
1 |
12 0. |
|
1 |
2 |
1 |
|
|
|
|
|
|
Прямые не лежат в одной плоскости, то есть скрещиваются.
Найдем угол между прямыми:
cos |
|
|
|
|
|
2 1 0 2 1 1 |
|
|
|
3 |
|
, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 2 02 12 12 22 1 2 |
30 |
|
|
||||||||
откуда arccos |
|
|
3 |
|
570. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
30 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Примеры для самостоятельного решения
1). Составить уравнение прямой, проходящей через точку M 1;1;1 и пер-
пендикулярной векторам N1 2i 3j k и N2 |
3i j 2k. |
||||||
Ответ: |
x 1 |
|
y 1 |
|
z 1 |
. |
|
|
1 |
|
|
||||
5 |
|
|
7 |
|
|||
2). Вычислить |
углы, |
образованные с |
осями координат прямой |
||||
x 2y 5 0,
x 3z 8 0.
Ответ: cos 6; cos 3; cos 2. 7 7 7
3). Найти уравнения прямой, проходящей через точку A 1; 2;3 и обра-
зующей с осями Ox и Oy углы 450 и 600 соответственно.
5

|
Ответ: |
x 1 |
|
|
|
y 2 |
|
z 3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4). |
Даны |
три |
последовательные вершины параллелограмма |
|
ABCD: |
||||||||||||||||||||||||
A 3;0; 1 , |
B 1;2; 4 и C 0;7; 2 . Найти уравнения сторон AD и СD. |
||||||||||||||||||||||||||||
|
Ответ: |
x 3 |
|
y |
|
z 1 |
; |
x |
|
y 7 |
|
z 2 |
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
1 |
5 |
|
|
2 |
|
|
2 2 |
3 |
|
|
|
|
|
|
|
|
|
|||||||||
5). |
Вычислить расстояние между параллельными прямыми |
x |
|
y 3 |
|
z 2 |
|
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
1 |
|
|||||
и |
x 3 |
|
y 1 |
|
|
z 2 |
. |
|
|
|
||
|
|
|
|
|
|
|||||||
1 |
2 |
1 |
|
|
|
|
|
|||||
|
|
Ответ: |
5 |
|
|
. |
|
|||||
|
|
30 |
|
|||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
6 |
|
|
|
|
|||
6). |
|
|
|
|
|
|
|
|
|
4x y z 12 0, |
3x 2y 16 0, |
|
Найти угол между прямыми |
и |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
y z 2 0. |
3x z 0. |
Ответ: cos 20 .
21
6
