
Практика 4
..pdf
Практика 4
ПРЯМАЯ НА ПЛОСКОСТИ
Прямая на плоскости в декартовой прямоугольной системе координат
Oxy может быть задана уравнением одного из следующих видов:
Ax By C 0 – общее уравнение прямой;
A x x0 B y y0 0 – уравнение прямой, проходящей через точку
M 0 x0;y0 перпендикулярно нормальному вектору N A;B ;
|
x x0 |
|
y y0 |
– каноническое уравнение прямой, где |
M 0 x0;y0 – точка |
|
|
|
|
||||
|
p |
|
q |
|
||
прямой, l p;q – направляющий вектор прямой; |
|
|||||
x x0 |
pt, |
|
||||
|
|
t ; .– параметрические уравнения прямой; |
||||
y y0 |
qt, |
|
||||
x y 1 – уравнение прямой в отрезках; a b
y kx b– уравнение прямой с угловым коэффициентом k tg , где –
угол, который составляет прямая с положительным направлением оси
Ox;
x x1 |
|
y y1 |
– уравнение прямой, проходящей через две точки |
x2 x1 |
|
||
|
y2 y1 |
||
M1 x1;y1 и M2 x2;y2 ; |
|||
y y0 |
k x x0 – уравнение прямой с угловым коэффициентом k, прохо- |
||
дящей через точку M 0 x0;y0 .
Угол между прямыми на плоскости:
|
|
|
|
|
|
|
|
|
|
N1 N2 |
|
|
|
|
k |
k |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
cos |
cos |
N ,N |
|
|
|
|
|
|
|
|
|
|
, или tg |
|
|
, |
||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 k1k2 |
|||||||||||||||
|
|
1 |
|
2 |
|
|
|
N |
N |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
где N1 , N2 - нормальные векторы прямых, k1, k2 – угловые коэффициенты пря-
мых.
Условие параллельности прямых:
|
|
|
|
|
|
|
|
|
|
A |
B |
|||||||
k |
k |
2 |
, или N |
|| N |
2 |
|
1 |
|
1 |
. |
||||||||
|
|
|
|
|
||||||||||||||
1 |
|
|
|
1 |
|
|
|
A |
B |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|||
Условие перпендикулярности прямых: |
|
|
|
|
|
|
|
|||||||||||
k1 k2 1 , или N1N2 |
0 A1A2 B1B2 0 . |
|||||||||||||||||
Расстояние от точки M |
0 x0;y0 |
до прямой Ax By C 0: |
||||||||||||||||
|
|
d |
|
|
Ax0 By0 |
C |
|
|
. |
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
A2 B2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 1.
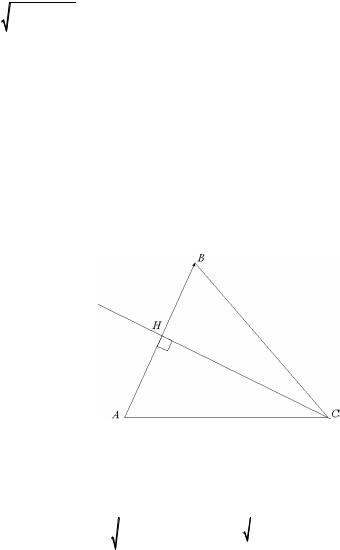
Составить уравнение высоты треугольника ABC, проведенной из точ-
ки C, и определить её длину, если A 0;1 , B 6;5 , C 12; 1 .
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Уравнение высоты CH треугольника ABC (рис.28) составим как урав- |
||||||||||||||||||||||
нение |
|
прямой, |
проходящей |
через точку |
|
|
|
|
|
|
|
|
|
|
|||||||||||
C 12; 1 |
с |
нормальным |
вектором |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
AB 6 0;5 1 6;4 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6 x 12 4 |
y 1 0, или 3x 2y 34 0. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Длину высоты |
CH |
находим как рас- |
|
|
|
|
|
|
|
|
|
|
||||||||||
стояние от точки C до прямой |
AB. Уравне- |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ние |
AB составим |
по |
точкам A 0;1 и |
B 6;5 : |
|
Рис.28 |
|||||||||||||||||||
|
x 0 |
|
y 1 |
, или |
2x 3y 3 0. Тогда |
|
CH |
|
|
|
2 12 3 1 3 |
|
|
|
30 |
|
. |
||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
6 0 |
|
5 1 |
|
|
|
|
|
|
|
|
|
|
|
22 3 2 |
|
|
13 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Составить |
уравнения |
биссектрис |
углов |
между |
|
прямыми |
||||||||||||||||
A1x B1y C1 0 и A2x B2y C2 0.
2

Решение.
Биссектриса угла – множество точек, равно-
удалённых от его сторон, то есть в данном случае,
от прямых A1x B1y C1 0 |
и A2x B2y C2 |
0. |
||||||||||||||||||||||||||
|
|
|
|
Точка |
|
M x;y |
принадлежит |
биссектрисе |
||||||||||||||||||||
тогда |
|
|
|
и |
|
|
|
|
|
|
только |
|
|
|
|
|
тогда, |
когда |
||||||||||
|
|
A1x B1y C1 |
|
|
|
|
|
A2x |
B2y |
C2 |
|
|
, |
|
или |
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
A2 |
B |
2 |
|
|
|
|
A2 B2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
1 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Ax B y C |
|
|
|
A x B y C |
2 |
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
1 |
1 |
|
|
|
|
2 |
|
2 |
|
|
0. |
Это и |
есть |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
A2 |
B2 |
|
|
A2 |
B2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
1 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
Рис.29 |
||||||||||||
уравнения обеих биссектрис. |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
Пример 3.
Составить уравнение прямой, проходящей через точку M 5;1 и обра-
зующей с прямой 2x y 4 0 |
угол |
|
. |
|
||
|
|
|||||
|
|
|
4 |
|
|
|
Решение. |
|
|
|
|
|
|
Угловой |
коэффициент |
данной |
|
|||
прямой |
2x y 4 0 равен |
–2. Тогда |
|
|||
угловой коэффициент k искомой прямой |
|
|||||
должен |
удовлетворять |
условию |
Рис. 30 |
|||
k 2 tg , откуда, учитывая равенство tg 1, получаем
1 2k |
4 |
4 |
k 3,
1
k .3
Таким образом, условию задачи удовлетворяют две прямые. Составим
уравнения этих |
прямых по угловому |
коэффициенту и точке M : |
|||
y 1 3 x 5 , |
|
3x y 14 0, |
|
||
|
1 |
|
|
|
|
|
x 5 |
, |
или |
|
|
y 1 |
|
x 3y 8 0. |
|
||
3 |
|
||||
|
|
|
|
|
|
3
Пример 4.
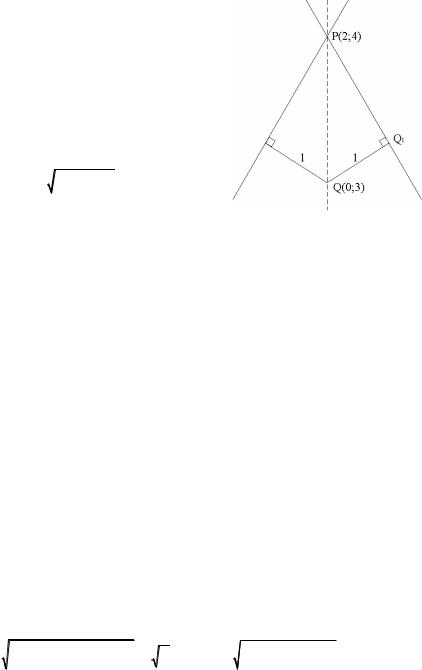
Написать уравнение прямой, проходящей через точку P 2;4 на рас-
стоянии 1 от точки Q 0;3 .
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 способ. Пусть Ax By C 0 – общее уравне- |
|
|
||||||||||||||||||
ние искомой прямой. Координаты точки P удовлетво- |
|
|
||||||||||||||||||
ряют этому уравнению: 2A 4B C 0. Расстояние от |
|
|
||||||||||||||||||
точки |
Q до прямой равно 1: |
|
|
0 A 3 B C |
|
|
1 , или |
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
A2 B2 |
|
|
||||||||
3B C 2 |
A2 B2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 31 |
||
Решаем систему |
2A 4B C 0, |
|
|
Для этого из первого уравнения |
||||||||||||||||
|
|
|
|
2 |
A |
2 |
|
2 |
. |
|||||||||||
|
|
|
|
3B C |
|
|
B |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выразим |
3B C 2A B и |
подставим во второе. Возведем полученное |
||||||||||||||||||
уравнение в квадрат: 3A2 4AB 0 и, |
учитывая первое уравнение, получим |
|||||||||||||||||||
A 0, |
C 4B; |
|
|
|
|
|
задачи |
|
удовлетворяют |
две |
прямые |
|||||||||
|
3 |
|
Условию |
|
|
|
|
|
||||||||||||
B |
A, |
C A. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4
By 4B 0, |
|
или |
y 4 0, |
||
|
3 |
|
|
||
|
|
|
|
4x 3y 4 0. |
|
Ax |
|
Ay |
A 0, |
|
|
|
|
||||
4
2 способ. Рассмотрим прямоугольный треугольник PQQ1, где Q1 – про-
екция точки Q на искомую прямую.
|
QQ1 |
|
1 по условию, |
|
PQ |
|
|
0 2 2 3 4 2 |
5, |
|
PQ1 |
|
|
|
PQ |
|
2 |
|
QQ1 |
|
2 2, |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
tg QPQ1 |
|
QQ1 |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
PQ1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4

|
Таким образом, задача сводится к |
тому, чтобы составить уравнение |
||||||||
прямой, проходящей через точку P 2;4 |
и образующей с прямой |
PQ угол |
||||||||
arctg |
1 |
(см. пример 3). Уравнение PQ (по 2 точкам): |
x |
|
y 3 |
, или |
y |
x |
3. |
|
|
||||||||||
|
|
|
|
|||||||
2 |
|
2 |
1 |
|
2 |
|
||||
|
Угловой коэффициент искомой |
прямой удовлетворяет |
условию: |
|||||||
1
k k2 12 , откуда
1 2
k 0,k 4.
3
Используя координаты точки P, записываем для каждого случая урав-
нение прямой с угловым коэффициентом y 4; |
y |
4 |
x |
4 |
. |
||
|
3 |
||||||
|
|
|
3 |
|
|
||
Пример 5. |
|
|
|
|
|
|
|
Известны уравнение стороны |
AB квадрата ABСD x 3y 3 0 и точ- |
||||||
ка пересечения диагоналей O 2;0 . Написать уравнение остальных его сто- |
|||||||
рон. |
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
Диагонали AC и BD проходят через |
|
|
|
|
|
||
точку O и образуют со сторонами квадрата |
|
|
|
|
|
||
углы в 45 . Как в примере 3 определяем их |
|
|
|
|
|
||
уравнения: |
y x/2 1 AC |
и |
|
|
|
|
|
y 2x 4 |
BD . |
|
|
|
|
|
Рис. 32 |
Координаты вершин A и B определяем как точки пересечения диаго-
x 3y 3 0 AB , |
||||
налей со стороной AB: A: |
x |
|
AC ; |
|
y |
|
1 |
||
2 |
||||
|
|
|
||
x 3y 3 |
0 AB , |
A 0;1 , |
B: y 2x |
4 (BD); |
B 3;2 . |
Канонические уравнения прямых AD и BC составим по точке и
направляющему вектору N 1;3 : |
x 0 |
|
y 1 |
|
AD , |
x 3 |
|
y 2 |
BC . |
1 |
|
|
1 |
|
|||||
|
3 |
|
|
3 |
|
||||
5
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
xA xC |
, |
откуда |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Точка O – середина отрезка AC, следовательно: 0 |
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
yA yC |
, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
C 4; 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Уравнение DC найдем по точке C и нормальному вектору N 1;3 : |
||||||||||||||||||||||
1 x 4 3 y 1 0, или x 3y 7 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Примеры для самостоятельного решения |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1). |
Написать уравнения сторон треугольника ABC, |
если задана его вер- |
|||||||||||||||||||||
шина |
A 1;3 и уравнения двух медиан |
x 2y 1 0 и y 1 0. Составить |
|||||||||||||||||||||
уравнение высоты AH этого треугольника. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Ответ: стороны: |
x 2y 7 0, |
x 4y 1 0, |
x y 2 0; |
|
|
высота: |
||||||||||||||||
4x y 7 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2). |
Дана точка |
M 1;2 и прямая L: |
2x y 1 0. Вычислить расстоя- |
||||||||||||||||||||
ние от точки M до прямой L. Записать уравнение прямой, проходящей через |
|||||||||||||||||||||||
точку M : а) перпендикулярно L; б) параллельно L; в) под углом /4 к L. |
|
|
|||||||||||||||||||||
|
Ответ: |
3 |
. |
а) |
x 1 |
|
|
y 2 |
; б) 2 x 1 y 2 0; |
в)y 3x 1, |
|
y |
x |
|
7 |
. |
|||||||
|
|
2 |
|
|
|
3 |
|||||||||||||||||
|
5 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||||
3). |
Даны две противоположные вершины квадрата A 1;3 и C 1;1 . Най- |
||||||||||||||||||||||
ти координаты двух других его вершин и написать уравнения сторон. |
|
|
|
|
|
||||||||||||||||||
|
Ответ: B 1;1 , D 1;3 , x 1 0 AB , |
y 1 0 BC , x 1 0 CD , |
|||||||||||||||||||||
y 3 0 AD .
4). Составить уравнение прямой, которая проходит через точку M 8;6 и
отсекает от координатного угла треугольник площадью 12.
Ответ: |
x |
|
y |
1, |
x |
|
y |
1. |
|
|
8 |
|
|||||
4 |
|
6 |
3 |
|
||||
5). Составить уравнения сторон треугольника, если известны координаты
их середин A1 1; 1 , B1 1;9 и C1 9;1 .
Ответ: x 5y 44 0 AC ; |
x y 2 0 BC ; |
5x y 44 0 AB . |
6
6). Определить расстояние от точки A 2; 1 до прямой, отсекающей на
осях координат отрезки a 8,b 6.
Ответ: 4,4.
7
