Лекция 3

второму виден против часовой стрелки.

В противном случае тройка векторов называется левой.

c

На рис. 21 тройка векторов

является правой, так как с

b

a,b,c

кратчайший поворот (т.е.

на угол ) от

0

a

конца вектора c

к вектору

происходит против часовой стрелки.

Рис. 21

вектора a

b

Тройка же

векторов

является левой,

так как

с конца третьего

вектора

b, a,c

поворот от первого

вектора

(вектора

второму

(вектора c ) кратчайший

b ) ко

вектору (вектору

a ) происходит по часовой стрелке.

меняется, т.е. ориентации троек (a,b,c) , (b,c, a) , (c, a,b ) − одинаковы.

Определение векторного произведения

Определение. Векторным произведением векторов

a

и b называется вектор

, удовлетворяющий трем условиям (рис.22):

c

c

1)

c

a

b

sin , где (a , b );

b

a

2) вектор c

перпендикулярен векторам a

и b ;

Рис.22

Обозначается векторное произведение

или

[a,b ]

a b . Заметим, что длина

вектора c равна площади параллелограмма, построенного на векторах a

и b .

Пример 2.8. Показать, что

i j k ,

i k j,

j k

i .

Решение.

Покажем,

что

Действительно,

k

i j k .

длина

вектора

единице,

т.е.

равна

площади

k равна

прямоугольника, построенного на векторах

и

Кроме

j

j

i

j .

i

того,

перпендикулярен векторам

Рис.23

вектор k

i , j и векторы

i ,

j, k

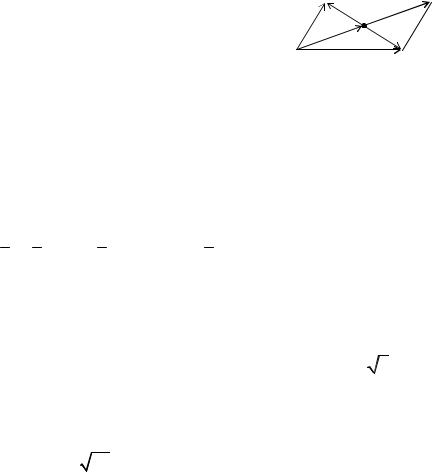
образуют правую тройку, так как с конца вектора k кратчайший поворот

от вектора i

к вектору

j происходит против часовой стрелки (рис.23).

Теперь

покажем,

что

1

, вектор

i k j. Действительно,

j

i k

j перпендикулярен векторам

i , k

и векторы i , k , j образуют правую тройку,

кратчайший поворот от вектора

так как с конца вектора j

i

к вектору k

происходит

против часовой

стрелки

(рис. 23).

Равенство

проверьте

j k

i

Докажем первое свойство:

0;

a b 0

a b

sin 0

sin 0

0

или ,

a

b

a

b

т.е. векторы a

и b коллинеарны.

Докажем второе свойство:

Действительно,

длины векторов

b

a

a b.

и

равны

(так

как

равны

площади

b

a

a b

параллелограммов, построенных на векторах

a b

a,b и b, a );

и

−

коллинеарны

(так

как

b

векторы b

a ,

a b

перпендикулярны

плоскости

векторов

и

и

a

b )

a

противоположно

направлены

(так

как

кратчайший

b

a

поворот (рис. 24) против часовой стрелки от

Рис. 24

a к b виден

с конца вектора

a b , а от b к

a

− с конца вектора a b ).

Доказательство третьего свойства опустим.

Из свойства линейности следует,

что при векторном умножении можно

Пример 2.9. Вычислить (i

j ) (i

j ).

Решение.

Раскроем

скобки, используя свойство

линейности

и сохраняя

порядок множителей:

(i

j ) (i

j ) i i j i

i

j j j.

0,

Из первого свойства следует, что i

i

j j 0. Из второго свойства и

примера

2.8

следует,

что

Окончательно

получим:

j i

i

j

k .

Заметьте,

что

при

векторном

умножении (в

отличие от

(i

j ) (i

j ) 2k .

векторы

и

Пусть в ортонормированном базисе i , j , k

a

b имеют

соответственно координаты {a1, a2 , a3}

и {b1,b2 ,b 3}. Это значит, что

a a 1 i a2 j a3 k ,

b b1 i b2 j b 3 k .

0.

Из первого свойства следует, что i i 0,

j j 0,

k k

Из второго свойства и примера 2.8 имеем:

i j k ,

i k j ,

j k i ,

j i k ,

k i j ,

k j i .

a b i (a2b3 a3b2 ) j (a1b3

a3b1) k (a1b2 a2b1) или

a

2

a

3

a

a

3

a

a

2

b

b

j

1

b

k

1

b

.

(2.19)

a b i

b

b

2

3

1

3

1

2

i

j

k

a1

a2

a3

.

(2.20)

a b

b1

b2

b3

В этой

формуле

{a1, a2 , a3}

− координаты

в

вектора a

базисе i , j , k ,

{b1,b2 ,b3} − координаты вектора

b

в базисе i , j , k .

Если разложить "определитель" в формуле (2.20) по элементам первой

строки, мы получим формулу (2.19).

, если

Пример 2.10. Вычислить a b

a 2i j 3k ,

b 3i j.

Решение. Векторы

имеют соответственно координаты

a и b в базисе i , j , k

{2, 1, 3} и {3, 1, 0}. Поэтому по формуле (2.20) имеем:

i

j

k

1

3

2 3

2 1

a b

2

1

3

i

1

0

j

3 0

k

3 1

3i 9 j k .

3

1

0

Пример 2.11.

Силы

F1 4i 2 j 7 k

и

F 2

2i j 3k

приложены к

точке

M (4, 3, 1).

Вычислить момент равнодействующей этих сил относительно

точки O(3, 1, 0).

Решение. Найдем равнодействующую сил F F1 F 2 {2, 1, 4} и вектор

r OM {1, 2,1}. Искомый момент m0

r

F вычислим по формуле (2.23):

i

j

k

1

2 1

m0

r F

9i 2 j 5k .

2

1

4

Пример 2.12. Вычислить площадь параллелограмма ABCD , если

AC 2e1 e2

BD 4e1 5e2

,

e1, e2

− единичные векторы и

(e1

, e

2 )

.

4