
Практика 2
..pdf
Практика 2
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
Вспомним понятие правой (левой) тройки векторов и ответим на вопрос: является ли изображённая на рис.7
тройка векторов a, b, c правой?
Ответ – нет. Так как поворот вектора a к вектору b с конца вектора c на угол φ (наименьший угол между векторами a и b) происходит по часовой стрелке, то тройка векторов a, b, c − левая.
Пример 1.
Вычислить j k , j i , i i .
Решение.
c
a
 φ
φ
Рис. 7 b
1). Покажем, что |
j k i . Сонаправленные векторы равны, если равны их |
|||||||||||||||
длины. Вектор |
j k |
сонаправлен вектору |
i , так |
|
||||||||||||
как |
j i , |
k i |
и поворот вектора |
j к вектору k с |
k |
|||||||||||
конца вектора i |
происходит против часовой стрел- |
|
||||||||||||||
ки (рис.8). Вычислим |
длину |
вектора |
j k : |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
1. Итак, вектор |
j |
|
|
j k |
|
j |
|
k |
sin |
1 1 1 1. |
|
|
|||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
i |
Рис.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
j k |
сонаправлен вектору |
i и имеет равную с ним |
k |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
длину, т.е. j k i .
2). Покажем, |
что |
j i k. Аналогично пункту (1) |
|
|
||||||||||
|
k |
|
1 и |
|
|
|
|
|
|
|
|
j i и k противо- |
|
|
|
|
j i |
|
j |
|
i |
sin |
1; |
|
j |
||||
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
Рис.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1

поi ложно направлены (поворот от вектора j к вектору i с конца вектора k
происходит по часовой стрелке, (рис. 9), следовательно, правую тройку обра-
зуют векторы |
j, i , k). |
|||||||||
3). Произведение |
i i 0, так как длина вектора равна нулю. Действи- |
|||||||||
тельно, |
|
|
|
|
|
|
|
|
2 |
sin0 1 0 0. |
|
|
|
|
|||||||
|
i i |
|
|
|
i |
|
|
|||
Пример 2.
Вычислить 5a b a b .
Решение.
Вычислим 5a b a b , используя свойства векторного произве-
дения: 5a b a b 5a a b a 5a b b b. Вспомним, что
a b b a и a a 0. Получим 5a b a b a b 5 a b 6 a b .
|
|
|
|
|
Пример 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Вычислить |
|
длину |
|
5a b a b , |
|
если |
известно, что |
|
a |
|
4, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
3 |
|
, а угол между векторами a и b равен 60˚. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Используя |
|
ответ задачи |
2, |
имеем |
5a b a b 6a b. |
|
Тогда |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
5a b |
|
|
|
a b |
|
|
|
|
|
a b |
|
|
a b |
|
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
6 |
6 |
|
|
|
sin a,b |
6 4 |
3 sin60 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
36. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
24 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Пример 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Вычислить |
|
a b |
|
, |
если a 2i j 6k, |
b j 3k . |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2

|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
По |
|
формуле |
вычисления |
векторного |
произведения |
|
векторов |
||||||||||||||||||||||
a a1;a2;a3 |
и |
b b1;b2;b3 |
|
в |
ортонормированном |
|
|
базисе: |
||||||||||||||||||||||
|
|
|
|
j |
k |
|
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
9 36 4 7. |
|||||||||||||||||||||||
a b |
a |
|
a |
a |
2 |
1 |
6 |
3i 6j 2k. Тогда |
|
|||||||||||||||||||||
|
|
1 |
|
2 |
3 |
|
0 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
b1 b2 b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Пример 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Вычислить площадь параллелограмма и площадь треугольника, по- |
|||||||||||||||||||||||||||||
строенных |
|
на |
векторах |
|
a m 2n, |
b m 3n , если |
|
m |
|
6, |
|
|
n |
|
3, |
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m,n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
a b |
|
|
||||||||||||||||||||||
|
Искомая |
площадь |
|
параллелограмма |
равна |
|
. |
Вычислим |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b m 2n m 3n m m 3m n 2n m 6n n 3n m 2n m 5n m.
При вычислении использованы свойства векторного произведения:
правило раскрытия скобок, a a 0, a b b a, a b a b a b .
Площадь параллелограмма
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
Sпар |
a b |
|
5n m |
5 |
n |
|
m |
sin n ^m 5 3 6 sin |
|
5 3 6 |
45. |
|||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
2 |
|
||
|
Площадь треугольника S , |
|
|
|||||||||||||||||||
|
построенного на тех же векторах a, b, |
|||||||||||||||||||||
|
1 |
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
равна |
|
|
Sпар, т.е. S |
|
22,5 . |
|
|
|
|
|
|
|
||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|||||||||||||
|
Пример 6. |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|||||
|
Найти расстояние от точки |
|
|
|
|
|
|
|||||||||||||||
|
A(0;4; 4) до |
d |
|
|
D |
|||||||||||||||||
прямой l , проходящей через точку B(3;4;2) |
|
|
||||||||||||||||||||
|
|
c |
||||||||||||||||||||
параллельно вектору c 2;1;2 . |
|
B |
|
|
Рис.10 |
|||||||||||||||||
3

Решение.
Поместим вектор c на прямую l , проходящую через точку B парал-
лельно вектору c, как на рис.10: BD c. Рассмотрим параллелограмм, по-
строенный на векторах BA и BD c. Расстояние d от точки A до прямой
l есть длина высоты параллелограмма, опущенной из точки A на сторону
BD. |
Площадь параллелограмма |
|
Sпар равна |
|
BD BA |
. Найдём координаты |
||||||||||||
вектора BA 3;0; 6 , вектор BD c 2;1;2 . Тогда |
|
|
||||||||||||||||
|
|
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
i |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
62 62 32 3 |
|
|
|||||||||||||
, |
|
|
4 4 1 9. |
|||||||||||||||
BD BA |
2 |
1 |
2 |
6i 6j 3k |
BD BA |
|
||||||||||||
|
|
3 |
0 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Итак, Sпар 9. Из геометрии известно, что Sпар BD d . Вычислим
BD c 
 4 4 1 3. Получим 3d 9 d 3 (расстояние от точки A до
4 4 1 3. Получим 3d 9 d 3 (расстояние от точки A до
прямой l ).
Пример 7.
Найти вектор m, зная, что он перпендикулярен векторам a 3;4;2 ,
b 0;2;1 , а скалярное произведение m c 12, где c 2i 3j k.
Решение.
По условию задачи m a, m b, следовательно, вектор m параллелен
вектору a b, который по определению векторного произведения, перпенди-
кулярен перемножаемым векторам a и b. Тогда m a b .
Найдём вектор a b: |
|
|
|
|
i |
j |
k |
|
|
|
, a b 0; 3; 6 . |
|
a |
|
b |
|
3 |
4 |
2 |
3j |
|
6k |
|
|
|
|
|
|
0 |
2 |
1 |
|
|
|
|
Координаты вектора m: |
m a b 0; 3 ;6 . Кроме того, по ус- |
||||||||||
ловию задачи m c 12. По формуле вычисления скалярного произведения векторов, заданных координатами в ортонормированном базисе, получим
4
m c 0 2 3 3 6 1 9 6 3 ; 3 12; 4.
Окончательно имеем вектор m 0; 12;24 .
Пример 8.
Сила F 2;2;9 приложена к точке A 4; 2; 3 . Определить момент
этой силы относительно точки B 3; 2; 1 .
Решение.
Известно, что момент mB F силы F, приложенной к точке A, относи-
тельно точки B, равен BA. Найдём координаты вектора BA.
|
|
|
|
i |
j |
k |
|
|
|
Тогда |
mB F |
1 |
0 |
2 |
4i 13j 2k. |
||||
|
|
|
|
2 |
2 |
9 |
|
|
|
Пример 9.
Точка A 1; 2; 3 вращается относительно 0;0;0 с постоянной угло-
вой скоростью w i j 2k. Найти координаты вектора линейной скорости точки A.
Решение.
Известно, что V A w rA, где rA − радиус-вектор точки A, V A − ли-
нейная скорость точки A.
|
|
|
rA 1;2; 3 |
|
|
|
i |
j |
k |
|
|
|
||||
Следовательно, |
и |
V A |
1 |
1 |
2 |
i j k . |
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
Пример 10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
a |
2, |
b |
5, |
|
|
|
. Выразить через векторы |
a и b еди- |
|||||||
a,b |
||||||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ничный вектор e , перпендикулярный векторам a, b и образующий с ними правую тройку a, b, e.
5

Решение.
Так как вектор e перпендикулярен векторам a и b, то он коллинеарен
векторному |
произведению |
этих |
|
|
|
|
векторов: |
e a |
|
и |
e b |
|
e, т.е. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
e a b . По условию задачи |
|
e |
|
|
1. Вычислим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
. |
||||||||||||
|
|
e |
|
|
|
a b |
|
|
|
|
|
a |
|
|
b |
sin a,b |
|
|
|
2 5 sin |
|
|
|
|
2 5 |
|
5 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Итак, 1 5 |
|
|
|
, |
|
|
|
|
1 |
. Тройка векторов a, b, e |
– правая, |
т.е. e a b, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
5 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
следовательно, |
|
|
|
и e |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Вычислить величину момента силы F 2a b, приложенной к точке A, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
относительно точки N, если NA a b, где |
|
6, |
3, a,b |
|
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|||||||||||||
|
|
Как известно, |
момент M0 F |
силы F, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
приложенной к точке A, относительно точки N |
N |
|
|
|
|
|
|
|
Рис. 11 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
равен M0 NA F (рис.11). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Величина момента M0 |
есть |
|
M0 |
|
, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0 |
|
|
|
NA F |
|
|
|
a b 2a b |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
Вычислим a b 2a b , используя свойства векторного произведе- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ния: |
|
a b 2a b 2a a a b 2b a b b a b 2a b 3a b, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6

|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.к. |
a a b b 0. |
Тогда |
|
||||||||||
M0 |
3a b 3 |
a b 3 |
b |
a sin a,b |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 6 3 sin 9 6 |
1 27. |
|
|
|
|
|
|
|
|
|
|||
|
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Итак, M0 F |
27. |
|
|
|
|
|
|
|
|
|
||
|
Пример 12. |
|
|
|
|
|
B |
|
|
|
|
C |
|
|
Прямая l проходит через |
|
h |
|
|
|
|
|
q |
||||
точку A(2; 1;0) параллельно век- |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
тору |
m 1;2;2 . |
|
Прямая |
q |
A |
|
|
|
|
|
|
|
|
проходит через точку |
B(2;3;2) |
|
|
|
D |
|
|
l |
|||||
|
|
|
|
|
|
||||||||
|
m |
|
|
|
|
|
|
||||||
параллельно тому же вектору. |
|
|
|
|
Рис. 12 |
|
|||||||
|
|
|
|
|
|
|
|
||||||
Найти расстояние между прямыми l и q . |
|
|
|
|
|
|
|||||||
Решение.
Поскольку обе прямые параллельны одному и тому же вектору, то прямые параллельны. Итак, задача состоит в определении кратчайшего рас-
стояния между параллельными прямыми. Один из способов решения этой за-
дачи состоит в вычислении длины высоты параллелограмма, две параллель-
ные стороны которого, например, AD и BC лежат на данных прямых l иq (рис.12). Определим координаты вектора AB 0;4;2 (из координат
конца вычтем координаты начала вектора). Известно, что AD m 1;2;2 .
|
|
i |
j |
k |
|
|
|
Вычислим: AB AD |
0 |
4 |
2 |
4i 2j 4k . |
|||
|
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
7

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sпар |
42 |
2 2 42 |
|
|
|
|
|
||||||||
|
Следовательно, |
AB AD |
16 4 16 6. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
С другой стороны |
Sпар h |
AD |
. |
Так как |
AD |
|
m |
|
|
1 4 4 |
3, то |
|||||||||
h |
Sпар |
6 |
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
AD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, расстояние между прямыми l и q равно 2.
Пример 13.
Найти вектор a, перпендикулярный векторам b i j k, c 2j k ,
если проекция вектора a на ось l, составляющую равные острые углы с ося-
ми координат, равна 2
 3 .
3 .
Решение.
В результате векторного умножения вектора b на вектор c получается вектор, перпендикулярный векторам-сомножителям, следовательно a||b c и
координаты искомого вектора a пропорциональны координатам векторного произведения b c.
|
|
|
|
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, b c |
1 |
1 |
1 |
i j 2k; a ; ;2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
0 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По |
условию |
ось |
l составляет равные углы |
с |
осями |
|
координат: |
|||||||||||||||||||||||||
. |
Тогда |
cos cos cos |
и равенство cos2 cos2 cos2 1 |
|||||||||||||||||||||||||||||
даст 3cos2 1. Отсюда, |
cos2 |
1 |
, |
cos |
1 |
|
|
, но поскольку по условию |
||||||||||||||||||||||||
3 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
углы α, β, γ – острые, то cos cos cos |
1 |
|
|
. Проекция на ось l |
совпа- |
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|||||
дает с проекцией на единичный вектор l0 оси l; l0 |
|
|
|
|
; |
|
|
|
|
; |
|
|
|
|
. Тогда |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3 |
3 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||
8

|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
пр |
a |
a,l0 |
|
|
( 2 ) |
|
. По условию задачи |
|
2 |
3 |
. Следова- |
||||||||
|
|
|
|
|
|
||||||||||||||
3 |
|
|
|
|
|
|
|||||||||||||
l0 |
|
|
|
3 |
|
|
3 |
|
|
|
|
||||||||
тельно, λ=3 и искомый вектор имеет координаты a 3; 3;6 .
|
Примеры для самостоятельного решения |
|
||
1). |
Даны векторы a 5i 3j 9k и b 4i 2j 7k . Вычислить проекцию |
|||
вектора c a b на ось, составляющую с координатными осями Oy, Oz |
||||
углы 120 , 135 , а с осью Ox– тупой угол . |
|
|||
|
Ответ: |
|
2 |
|
|
2 |
|
||
2). |
Вектор x, перпендикулярный к векторам a 3, 3,3 |
и b 2,1, 3 , |
||
образует с осью Oy тупой угол. Зная, что x 2
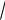 6 , найти его координаты.
6 , найти его координаты.
Ответ: x (4; 2;2).
3). Найти площадь треугольника, построенного на векторах c |
4a b и |
||||||||
d a 2b , если |
|
a |
|
|
|
4, а угол между векторами a и b равен 450 . |
|||
|
|
|
5, |
b |
|||||
|
|
||||||||
Ответ: 45 |
|
|
|
|
|
|
|||
2 |
|
|
|
|
|||||
9
