Лекция 2

,

если

A B

A B

с

прc AB прl AB

.

(2.8)

A B

,

если

A B с

1) пр c AB

AB

cos ,

где − угол между векторами AB и c

;

2) пр c ( a b ) пр с a пр с b ;

Определение. Скалярным произведением векторов

a

и b называется

число

a b , равное произведению длин этих векторов на косинус угла между

ними:

a b

a

b

cos .

Принято также и другое обозначение скалярного произ-

ведения

b

(a,b ) .

Отметим,

что если

то 0

и

из

определения

следует, что

b

a ,

2

. Произведение

2

и называют скалярным квадра-

a

a

a

a a обозначают

a

том вектора. Итак,

2

2

.

a

a

Свойства скалярного произведения

1). Скалярное произведение ненулевых векторов равно нулю тогда и

только тогда, когда эти векторы перпендикулярны.

2). Скалярное произведение векторов коммутативно:

a b b

a.

3). Скалярное произведение ненулевых векторов связано с их проекция-

ми:

пр

a b

a

пр b

b

a.

a

b

4). Свойство линейности:

( a b ) c

(a c) (b

c),

a ( b c)

(a b ) (a

c).

Докажем первое свойство: для ненулевых векторов

a b

a

b

cos 0

cos 0

a b.

2

Доказательство второго свойства основано на том,

что углы (a , b ) и

(b , a) равны, поэтому a b

a

b

cos(a , b )

b

a

cos(b , a) b a.

Доказательство третьего свойства следует из того, что

a

cos (a , b ) пр a,

b

cos (a , b ) пр

b.

b

a

Поэтому

пр

a b

a

b

cos (a , b )

a

пр b

b

a.

a

b

Например,

2

(a b )

(a b ) (a b ) a

a

a b b

a b b, то есть для

векторов, как и для чисел, справедлива формула

2

2

2

.

(2.9)

(a b )

a

2 a b b

Аналогично (проверьте самостоятельно),

2

2

.

(2.10)

(a b )

(a b ) a

b

Пример 2.4. Известно, что

3

a

2,

b

3,

(a , b )

. Вычислить

4

(a 3b ) (2 a b ).

2

2

.

(a 3b ) (2 a b ) 2 a

a

a b 6b

a 3b b 2

a

5a b 3

b

2

Так как a b

a

b

cos (a , b )

2 3

3

, то

2

(a 3b ) (2a b ) 2 2 5 3 3 9 8 .

Вычисление скалярного произведения в ортонормированном базисе

Рассмотрим ортонормированный базис i , j , k . Пусть

a a1 i a2 j a3 k ,

b b1 i b2 j b3 k .

Найдем скалярное произведение этих векторов,

используя

свойство линейности:

a b (a1i

a2 j

a3k ) (b1i

b2 j b3k )

a1b1(i ,i ) a1b2 (i , j ) a1b3 (i , k ) a2b1(j,i) a2b2(j, j) a2b3(j, k)

a3b1(k ,i) a3b2(k , j) a3b3(k , k).

a1, a2 , a3 1,0,0

a1

a i

cos

1

.

a

i

a

a

Возводя

в

квадрат и

складывая

равенства (2.15), учитывая,

что

2

2

2

2

, получим формулы (2.16).

a 1

a2

a 3

a

5). Вычисление проекции для ненулевых векторов a

и b

a b

пр a b

.

(2.17)

a

Эта формула следует из свойства 3) скалярного произведения.

6). Вычисление работы A постоянной силы F при прямолинейном пере-

мещении из точки M в точку N (рис.18).

.

(2.18)

A F MN

Действительно, из физики известно, что

F

A

F

MN

cos (F , MN ), а значит,

A F MN .

M

N

Решение. Сделаем схематичный чертеж (рис.19).

B

C

Найдем координаты векторов AB ,BD и

AD ,

вычитая

0

D

A

из координат концов координаты начала этих векторов:

Рис. 19

AB { 3, 1,1},

BD 5,-2, 2 , AD {2, 3,3}.

По правилу параллелограмма

AC AB AD { 1, 4, 4}.

1 5 ( 4) ( 2) 4 2

11

1

AC BD

cos

.

3

AC

BD

( 1)2 ( 4)2 42

52 ( 2)2 22

33 33

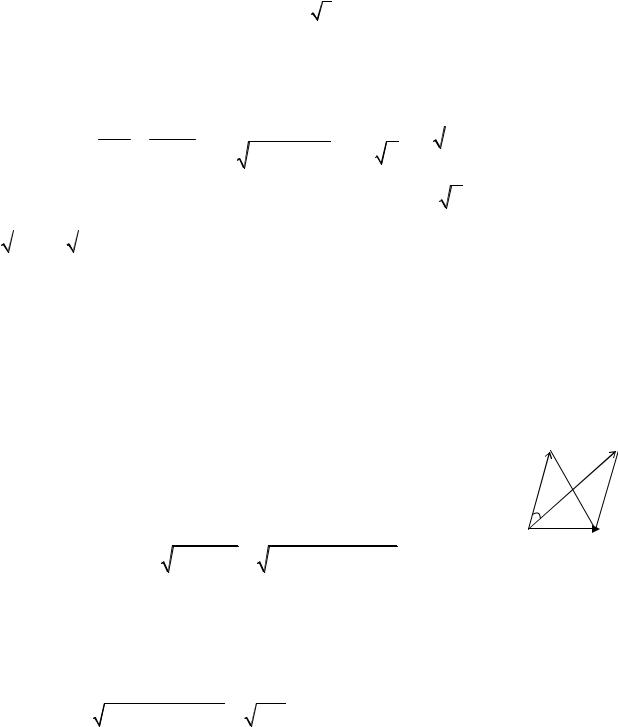
Заметим, что

, т.е. диагонали параллелограмма равны, следо-

AC

BD

из условия перпендикулярности векторов AB и AD , так как их скалярное про-

изведение равно нулю:

AB AD 3 2 ( 1) ( 3) 1 3 0.

Пример 2.6.

Найти вектор

, если его

c

, коллинеарный вектору a {1,3, 2}

проекция на вектор b {2,1,0} равна

2

5.

Решение. Так как вектор c

коллинеарен вектору a

, то c a . Вычислим

проекцию вектора

c

на вектор b по формулам (2.17) и (2.11):

c b

a b

(1 2 3 1 2 0)

5