
Лекция 1
.pdf
Лекция 1
ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКА
Рассмотрим прямоугольную таблицу чисел, состоящую из к строк и n
столбцов, заключенную в круглые скобки
|
a11 |
a12 |
... |
a1n |
|
|||||
|
a |
21 |
a |
22 |
... |
a |
|
|
|
|
A |
|
|
|
|
2 n |
. |
||||
... |
... |
... |
... |
|
||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
am2 |
... |
|
|
|
|
||
|
am1 |
am n |
|
|||||||
Эту таблицу называют матрицей. Элемент матрицы a i j имеет два индекса i
иj , где i – номер строки, j – номер столбца, на пересечении которых
расположен элемент a i j .
Если число строк равно числу столбцов, то матрица называется квадратной.
Любой квадратной матрице можно поставить в соответствие число, вычисляемое
по определенным правилам и называемое определителем.
Определитель второго порядка − это число
|
|
|
|
|
|
|
a11 |
|
a12 |
a 11 a22 a 12 a21 . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
a21 |
|
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
Определитель третьего порядка – это число |
|
|
|
|
|
|
|
|||||||||||||||
|
a11 |
a12 |
a13 |
|
|
|
|
a22 |
a23 |
|
|
a21 |
a23 |
|
|
|
a21 |
a22 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a |
|
a |
|
a |
|
a |
|
|
a |
|
|
a |
|
. |
|||||||
|
|
21 |
|
22 |
|
23 |
|
|
11 |
|
a32 |
a33 |
12 |
|
a31 |
a33 |
|
13 |
|
a31 |
a32 |
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Число равно сумме слагаемых (знаки этих слагаемых чередуются,
начиная со знака +), в которых каждый элемент первой строки умножается на определитель, который получается вычеркиванием той строки и того столбца, на пересечении которых стоит этот элемент. Например,
1

4 |
2 |
3 |
|
3 |
1 |
|
2 |
1 |
|
2 |
3 |
|
|
|
|
|
|||||||||
2 |
3 |
1 |
4 |
2 |
3 |
4(3 1 6 1) 2( 2 1 1 1) 3( 2 6 1 3) 51. |
||||||
1 |
6 |
1 |
|
6 |
1 |
|
1 |
1 |
|
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
Аналогично вычисляется определитель n–го порядка. Эти определители и свойства определителей мы рассмотрим в п.5.2. Для изучения векторной алгебры и аналитической геометрии достаточно уметь вычислять определители лишь второго и третьего порядка.
ВЕКТОРНАЯ АЛГЕБРА
В различных дисциплинах используются скалярные и векторные величины.
Скалярная величина определяется одним числом, например, масса, объем,
температура. Векторная величина характеризуется не только числом, но и направлением, например, сила, скорость, ускорение. Отвлекаясь от конкретного содержания, векторная алгебра изучает геометрические векторы и операции над ними.
2.1. Понятие вектора
Понятие вектора, линейные операции над векторами были рассмотрены в
школьном курсе математики. Напомним основные моменты.
В |
математике |
вектор |
− это |
направленный отрезок. |
|
|
|
|
B |
||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Направление указывают стрелкой (рис.1); различают начало |
|
|
|
a |
|
||||||||||||||
A |
|
||||||||||||||||||
вектора |
А и его конец |
|
|
|
|
его |
|
Рис. 1 |
|||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||
В. Обозначают вектор a, AB, |
|
|
|
|
|
||||||||||||||
длину a, |
|
|
|
|
|
Если начало и конец вектора совпадают, то вектор называют |
|||||||||||||
|
a |
, |
|
AB |
. |
||||||||||||||
нулевым и обозначают |
|
Его направление считается произвольным, а длина – |
|||||||||||||||||
0. |
|||||||||||||||||||
нулевой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
векторы |
|
параллельны |
одной |
прямой, |
то они |
называются |
||||||||||||
коллинеарными. |
При |
этом |
векторы могут быть направлены в |
одну сторону |
|||||||||||||||
(сонаправлены), |
или |
− |
в |
разные |
стороны |
( противоположно |
направлены). |
||||||||||||
Записывают это так: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a b |
или a b . |
|
|
|
|
|
|
|
|||||||||||
2
|
|
|
Векторы, параллельные одной плоскости, называются компланарными. |
|||||||
|
|
|
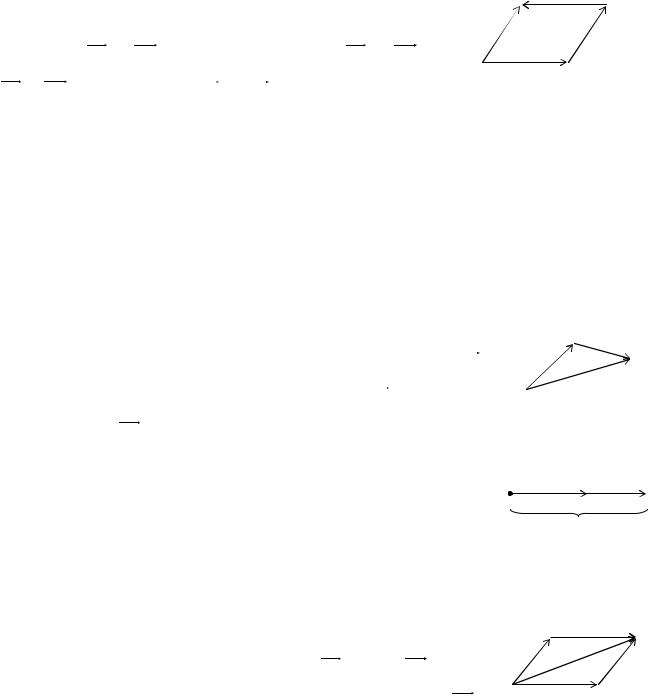
В математике два вектора называются равными, |
|
|
|||||
если они имеют одинаковые длины, |
коллинеарны и |
B |
|
|||||||
сонаправлены. На рис.2 в параллелограмме ABCD |
C |
|||||||||
|
|
|||||||||
векторы |
AB и DC − равны, |
так |
как AB DC и |
|
D |
|||||
|
|
|
|
|
|
|
|
А |
|
|
|
AB |
|
DC |
, |
а векторы CB и |
AD |
не |
равны, так как |
Рис.2 |
|
|
|
|
|
|
|
|
|
|
|
|
CB AD . |
|
|
|
|
|
|
||||
2.2. Линейные операции над векторами
Клинейным операциям относятся сложение, вычитание векторов,
умножение вектора на число.
Сложение векторов
Для сложения двух неколлинеарных векторов |
|
|
|
|
|
|
|
|||||||
a и b |
|
|
B |
|
||||||||||
отложим |
от какой-нибудь точки А (рис.3) |
вектор |
AB , |
|
|
b |
C |
|||||||
a |
|
|
|
|||||||||||
|
|
|
||||||||||||
равный |
|
, затем от точки В отложим вектор BC |
|
|
|
A |
|
c |
|
|
||||
a |
, равный b . |
Рис.3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда вектор |
AC |
называют суммой векторов |
Это |
|
|
|
|
|
||||||
a и |
b . |
|
|
|
|
|
||||||||
правило |
|
сложения |
двух |
векторов |
называют |
правилом |
|
|
|
|
|
|||
треугольника. |
По |
этому |
же правилу складываются |
и |
|
B |
|
|||||||
A |
a |
b |
C |
|||||||||||
коллинеарные векторы (рис.4), хотя при их сложении и не |
|
|
|
|
|
|||||||||
|
a b |
|
|
|||||||||||
получается треугольника. |
|
|
|
|
|
|
|
Рис.4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
Для сложения двух неколлинеарных векторов можно |
|
|
|
|
|
|||||||||
пользоваться также правилом параллелограмма: от какой- |
|
B |
|
|
C |
|||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
|
||||
нибудь |
точки |
А отложить векторы |
AB a и |
AD b |
и |
|
|
|
|
|
||||
|
|
|
|
|
||||||||||
построить параллелограмм ABCD (рис.5). Тогда вектор |
|
A |
|
D |
|
|||||||||
AC |
b |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Рис.5 |
|
|
|
равен a b . |
|
|
|
|
|
|
|
|
|
|
|
|
||
Сложение более двух векторов производится |
по |
|
|
|
|
|
||||||||
правилу |
|
многоугольника. |
Например, |
для сложения |
четырех векторов |
|
||||||||
|
a, b, c, d |
|||||||||||||
3
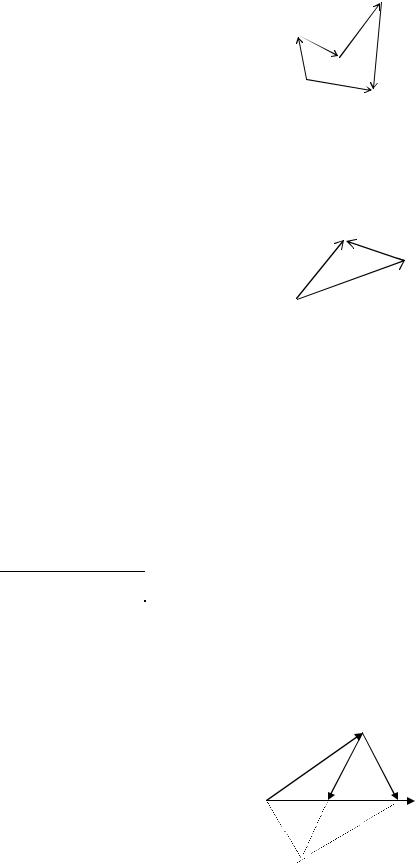
(рис.6) от произвольной точки A откладываем |
|
|
, затем из точки B |
|||||||
вектор AB a |
||||||||||
|
|
|
|
|
|
|
|
|
|
D |
откладываем вектор BC b , из точки C откладываем CD |
c , |
|
|
|||||||
|
|
|
|
|
|
|
|
B |
|
|
из точки |
|
|
|
|
c |
|||||
D откладываем вектор DK d . Тогда вектор |
AK |
|
b |
|
||||||
|
|
|
|
|
|
|
|
C |
||
(направленный из начала первого вектора к концу последнего) |
a |
|
d |
|||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
A |
|
K |
равен a b |
c d . |
|
|
|
|
|
|
|||
Рис.6
Вычитание векторов
Разность |
|
|
|
|
|
|
такой, что |
|
|
a b векторов |
a и |
b есть вектор |
c |
|
|||||
|
|
|
|
|
|
|
|
|
|
построения вектора a b из произвольной точки O отложим |
|
||||||||
|
|
и |
|
|
|
Тогда вектор разности |
|
||
векторы OA a |
OB b (рис. 7). |
||||||||
есть вектор |
|
|
|
|
|
|
и |
|
a |
BA , соединяющий концы векторов a |
b и |
|
|||||||
|
|
|
|
|
|
|
|
O |
|
направленный к вектору a . |
|
|
|
|
|
||||
Умножение вектора на число
|
|
|
|
. Для |
b |
c |
a |
||
|
A |
|
|
|
|
a |
b |
||
B
b
Рис.7
|
Произведением ненулевого |
вектора |
|
число |
|
называется |
вектор |
||||||||||||||
|
a на |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
a , такой, что |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1) |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
a |
2) b a, если 0, |
b |
a, если 0. |
|
|||||||||||||
|
Нетрудно |
проверить, |
что |
два ненулевых вектора |
|
|
|
||||||||||||||
|
a |
и b коллинеарны |
|||||||||||||||||||
тогда и только тогда, когда существует единственное число |
|
|
|
||||||||||||||||||
такое, что a b : |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
(2.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
a || b |
a b |
|
|
|
|
|
||||
Линейные операции над векторами обладают теми же свойствами, что и
линейные операции над действительными числами, т.е., можно группировать векторы и раскрывать скобки, как при действии с действительными числами.
|
Пример 2.1. В ABC известны векторы |
|
|
, |
|
|
|
B |
||
|
AB a |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
BC b , BK - медиана (рис.8). Найти вектор |
BK . |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
C |
|
|
|
|
|
|
|
К |
|
||
|
|
|
|
|
|
|
|
|
|
|
D Рис.8
4

Решение. Рассмотрим параллелограмм ABCD . Так как точка K есть
середина AC , то она является точкой пересечения диагоналей. Поэтому
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
BK |
|
|
BD |
|
(BC BA) |
|
(BC AB) |
|
(b |
a) . |
||
2 |
2 |
2 |
2 |
|||||||||
2.3. Координаты вектора и точки в заданном базисе
Разложение вектора по базису на плоскости Базис на плоскости – это упорядоченная пара неколлинеарных векторов
e1, e2 .
|
Пусть a − произвольный вектор на плоскости. Из |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
произвольной точки O отложим векторы, равные e1, e2 |
|||||||
|
|
|
|
|
|
|
|
OA a |
(рис. 9). Вектор OB коллинеарен вектору |
e1 , |
а |
||||
|
|
|
|
|
|
|
|
вектор |
OC коллинеарен вектору |
e 2 . |
Поэтому найдутся |
||||
|
|
|
|
|
|
|
|
такие числа a1 и a2 , что OB a1e1, |
OC |
a2e2. Тогда |
|
|
|||
C |
|
|
A |
|
|
||
|
|
|
|
e2 |
B |
||
O e1 |
|||
|
|
|
|
Рис.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.2) |
|
|
|
|
a |
a1e1 a2e2 . |
|
|
|
|
|
|
|
|||
Говорят, что |
|
разложен |
по |
|
а |
коэффициенты |
|||||||
вектор a |
базису e1, e2 , |
||||||||||||
разложения a 1, a 2 |
называют |
координатами |
вектора |
|
в |
базисе |
|
|
|
||||
a |
e1, e 2 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что разложение вектора a по базису |
e |
1, e 2 единственно. |
|
|
|
||||||||
Разложение вектора по базису в пространстве |
|
|
|
|
|
|
|||||||
Базис в пространстве – |
|
|
|
|
|
|
|
|
|
|
, |
||
это три некомпланарных вектора e1 |
, e2 |
, e3 |
|||||||||||
взятых в определенном порядке.
|
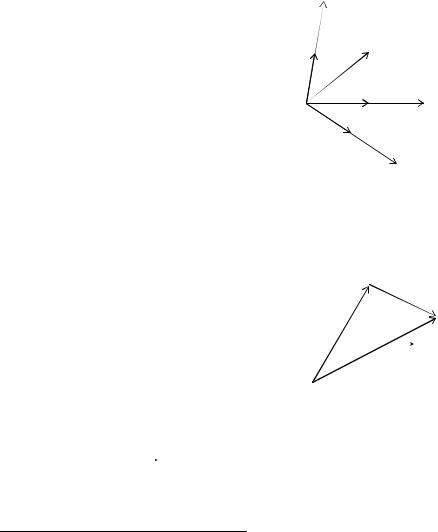
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
a произвольный вектор. Из произвольной |
|||||||||||
|
|
|
|
|
|
|
|
|
|
(рис. 10). |
||
точки O отложим векторы e1, |
e 2 , |
e3 |
и OA a |
|||||||||
Из |
точки |
A |
проведем |
прямую |
|
AB , |
параллельную |
|||||
вектору |
|
, |
до пересечения |
с |
плоскостью векторов |
|||||||
e 3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e1, |
e 2 . |
По |
правилу |
треугольника |
OA OB BA . |
|||||||
|
|
|
a |
|
|
e3 |
|
|
e2 |
|
|
О |
|
B |
|
e1 |
|
|
Рис.10 |
|
Как |
показано |
выше, |
5

|
|
|
|
|
|
|
|
|
|
|
|
|
OB a 1e1 a2 e2 |
. Вектор BA коллинеарен вектору e 3 , поэтому найдется число a3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
такое, что BA a3 e3. Тогда |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
(2.3) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
a |
a1 e1 |
a2 e2 |
a3 e3 . |
|
|
|||
|
Вектор |
разложен |
по базису |
|
|
|
|
; |
коэффициенты разложения |
|||
|
a |
e |
1, e 2 |
, e3 |
||||||||
a 1, a2 , a 3 есть координаты вектора |
|
|
|
|
|
|
||||||
a в базисе e |
1, e 2 |
, e 3 . |
||||||||||
Принята запись a a1, a2 , a3
a1
или a a2 .
a3
Свойства координат векторов
1). При умножении вектора на число его координаты умножаются на это же число.
2). При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются).
3). Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны.
Проверим третье |
свойство. |
Пусть в |
базисе |
|
|
|
|
имеет |
|||||||||||
e1, e 2 |
, e 3 вектор |
a |
|||||||||||||||||
координаты |
a 1, a2 , a 3 , |
|
|
|
|
|
|
|
|
b1, b2 , b 3 . Векторы |
|
|
|||||||
вектор b − координаты |
a |
и b |
|||||||||||||||||
коллинеарны тогда и только тогда, когда |
|
|
Используя первое свойство, |
||||||||||||||||
a b . |
|||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 b2 , |
a3 |
b3. |
|
|
|
(2.4) |
||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
a || b a1 b1, |
|
|
|
|
||||||||||||
Это |
и |
означает |
пропорциональность |
координат |
|
|
|
|
Если |
||||||||||
векторов a и |
b . |
||||||||||||||||||
b1, b2 , b 3 |
отличны от нуля, то эти соотношения записывают в виде |
|
|
||||||||||||||||
|
|
|
|
|
|
|
a 1 |
|
a 2 |
|
|
a 3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
b 2 |
b 3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6
Эти же соотношения записывают, если одна из координат вектора b равна нулю. Тогда из равенств (2.4) следует, что соответствующая координата вектора
тоже равна нулю. Итак,
a
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
2 |
|
|
a |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a || b |
1 |
|
|
|
|
|
. |
|
|
|
|
(2.5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
b |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|||
|
Координаты точки. Их связь с координатами вектора |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, поместим |
|
|
|||||||
|
Рассмотрим базисные векторы e1, |
e |
2 , e3 |
z |
|
|||||||||||||||||||||||
их в общее начало – фиксированную точку O (начало |
A |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координат). Через точку O и базисные |
|
векторы e3 |
rA |
|
||||||||||||||||||||||||
проведем оси координат Ox, Oy, Oz (рис. 11). |
|
|
|
|
|
|
O |
|
y |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Рассмотрим точку |
A . |
Вектор |
|
|
называют |
e2 |
|
||||||||||||||||||||
|
|
OA |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
точки А (рис.11), а его координаты |
e1 |
|
||||||||||||||||||
радиус-вектором rA |
Рис.11 |
x |
||||||||||||||||||||||||||
− координатами точки А в |
|
|
|
|
|
|
|
|
|
|
в |
|
|
|||||||||||||||
базисе e1, e 2 |
,e 3 или |
|
|
|||||||||||||||||||||||||
системе |
координат |
Oxyz . |
|
Координаты вектора будем |
A |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
писать |
в |
|
фигурных |
скобках |
OA {a1, a2 , a3} , |
а |
|
|
||||||||||||||||||||
координаты точки – в круглых скобках A(a1, a2 , a3 ) . |
|
rA |
B |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rB |
|||
|
Выразим |
координаты |
вектора |
|
|
AB |
|
через |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A(a1, a2 , a3 ) |
|
|
|
|
|
|
O |
|
|
||||||
координаты |
|
его |
начала |
|
и |
|
конца |
Рис.12 |
||||||||||||||||||||
B (b1,b2 ,b3 ). |
|
|
Радиус-векторы |
|
|
этих |
|
|
|
|
точек |
|
|
|||||||||||||||
r |
{a , a |
2 |
, a |
}, |
r {b ,b ,b }. |
Вектор |
AB соединяет концы этих векторов (рис. |
|||||||||||||||||||||
A |
1 |
|
|
3 |
|
B |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
12), следовательно, |
|
|
r |
и по свойствам координат векторов |
|
|||||||||||||||||||||||
AB r |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
B |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 , b3 |
a3}. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
AB {b1 a 1, b2 |
|
|
|
(2.6) |
||||||||||||||
Таким образом, для отыскания координат вектора надо из координат
конца вычесть соответствующие координаты начала.
Методами векторной алгебры удобно решать целый ряд геометрических задач. Поясним это на примере задачи деления отрезка в данном отношении.
7

Пусть известны координаты точек A(a 1, a2 , a3 ) и
B(b1,b2 ,b3) . |
Требуется |
|
найти |
|
координаты |
точки |
||||||
C(c1,c2 ,c3 ) , |
делящей отрезок |
АВ в |
отношении |
|||||||||
(рис.13). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AC |
|
|
|
|
|
|
|
||
По условию |
|
|
|
или |
|
AC |
|
CB |
. |
Кроме |
||
|
|
|||||||||||
|
|
|
CB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A
C
rA
rC
O |
B |
rB |
|
|
Рис.13 |
|
|
|
|
|
− сонаправлены. |
|
|
|
|
|
|
|
Рассмотрим |
|||||||||||||||
того, векторы AC |
и CB |
|
|
Поэтому AC CB . |
||||||||||||||||||||||||
(рис.13) радиус-векторы r |
|
, r , |
r |
точек A, |
|
|
|
|
|
|
|
|
|
r , |
|
r |
||||||||||||
|
B, C . Тогда AC r |
CB r |
||||||||||||||||||||||||||
|
|
|
A |
|
B |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
A |
B |
C |
|||
|
|
|
|
|
|
|
|
|
|
r |
(r |
|
r ) . Из этого соотношения |
|||||||||||||||
и равенство AC CB примет вид: r |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C |
A |
|
|
|
В |
|
С |
|
|
|
||||||||
|
|
r |
r r r |
|
или |
r |
|
rA rB |
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
C |
|
|
A |
|
|
В |
|
С |
|
|
|
|
|
C |
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогичными соотношениями связаны и координаты точек A, B, C : |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
c |
a1 b1 |
, |
c |
2 |
|
a2 |
b2 |
, |
|
c |
|
|
a3 b3 |
. |
|
|
(2.7) |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1 |
1 |
|
|
|
|
|
1 |
|
|
|
3 |
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если точка С делит отрезок АВ пополам, то 1 и |
|
|
|
|||||||||||||||||||||||||
|
|
c |
a1 b1 |
, |
|
c |
a2 b2 |
, |
|
c |
a3 b3 |
. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 2.2. Отрезок, соединяющий точки A(3, 2,1)
на пять равных частей (рис. 14). Найти координаты точки C2 .
Решение. Точка C2 (x, y, z) делит отрезок АВ в
отношении AC2 2 .
C2B 3
и B(15,6, 1) , разделен
A
C1
C2
C3
Найдем координаты точки C2 по формулам: |
Рис.14 |
С4 |
B |
|
|
8
|
a1 b1 |
|
|
3 |
2 |
|
|
15 |
|
a2 |
b2 |
|
2 |
2 |
6 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
|
|
|
3 |
|
|
|
|
|
|
|
7.8, |
y |
|
|
3 |
3.6, |
|
|
||||||||||
|
1 |
|
|
2 |
|
|
|
1 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
a3 b3 |
|
1 |
|
|
( 1) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
z |
|
|
3 |
|
|
|
|
|
0.2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
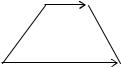
Пример 2.3. |
|
В трапеции |
ABCD (рис. 15) известны координаты трех её |
||||||||||||||||||||||||
вершин |
A(1,1, 4), B(3, 2, 1),C(4,3, 4). Найти координаты вершины D , |
если она |
|||||||||||||||||||||||||||
лежит в плоскости YOZ . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Решение. |
Так как |
вершина D |
лежит в плоскости YOZ , то её первая |
||||||||||||||||||||||||
координата |
|
x 0 , |
две другие координаты неизвестны, обозначим их y , z. |
Итак, |
|||||||||||||||||||||||||
точка D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
||
имеет координаты D(0, y, z) . Найдем координаты векторов AB |
DC, |
||||||||||||||||||||||||||||
вычитая из координат конца координаты начала:
|
2 1 , 1 4} |
{2,1,3}, |
|
3 y, |
4 z}. |
AB {3 1, |
DC {4, |
|
|
|
то их |
|
|
||||||
Так как векторы |
AB и |
DC коллинеарны, |
A |
B |
|||||||
|
|
|
|
|
|
|
|
|
|
||
соответствующие координаты пропорциональны, т.е. |
|
|
|||||||||
|
4 |
|
3 y |
|
4 z |
. |
D |
|
C |
||
2 |
|
|
3 |
Рис.15 |
|||||||
1 |
|
|
|
|
|
||||||
Тогда 2 3 y, |
2 |
4 z |
|
или z 2, y 1 |
и D(0,1, 2) . |
|
|
||||
|
|
|
|||||||||
|
|
3 |
|
|
|
|
|
|
|
||
9
