
Вопросы к экзамену
.docВопросы к экзамену
«Векторная алгебра и аналитическая геометрия»
Вопросы
Векторная алгебра. Вектор, равенство векторов. Сумма векторов, произведение вектора на скаляр. Проекция вектора на ось, свойства проекции. Линейная зависимость векторов. Базис.
Скалярное, векторное и смешанное произведения векторов, их свойства, применение и вычисление.
Аналитическая геометрия. Уравнение прямой на плоскости и в пространстве. Плоскость в пространстве. Расстояние от точки до прямой на плоскости и расстояние от точки до плоскости в пространстве.
Взаимное расположение прямых и плоскостей. Угловые соотношения между ними.
Кривые второго порядка в декартовой и полярной системах координат .
Поверхности 2-го порядка. Метод сечений.
Комплексные числа. Алгебраическая, тригонометрическая и показательная формы записи комплексного числа. Формула Муавра, извлечение корня n-ой степени.
Многочлены. Неприводимость многочленов над различными числовыми полями. «Основная теорема алгебры», теорема Безу.
Матрицы. Определение и частные виды матриц. Операции над матрицами. Свойства умножения матриц. Понятие определителя матрицы n-го порядка.
Теоремы аннулирования и разложения по любой строке. Минор, алгебраическое дополнение. Формулы Крамера для систем линейных уравнений.
Обратная матрица. Критерий существования обратной матрицы. Вычисление обратной матрицы с помощью присоединенной. Применение обратной матрицы к решению матричных уравнений. Метод Гаусса.
Определение линейного пространства, примеры. Подпространства, критерий подпространства. Базис и размерность. Линейная зависимость арифметических векторов.
Ранг матрицы. Инвариантность ранга матрицы относительно элементарных преобразований.
Определение СЛУ, совместность, однородность. Общее решение СЛУ. Теорема Кронекера-Капелли.
Однородные СЛУ. Теоремы о линейных комбинациях решений ОСЛУ, о пространстве решений ОСЛУ. Фундаментальная система решений ОСЛУ. Теорема об общем решении неоднородной СЛУ.
Типовые задачи
1. Даны две смежные вершины квадрата A(1, -2) и B(2, 3). Вычислить его площадь.
2. Даны три вершины A(4, 6), В(10, -10), С(-2, –2) параллелограмма АВСD, четвертая вершина D противоположна В. Определить длину диагоналей этого параллелограмма.
3. Найти координаты точки М1, симметричной точке М2(-2, 5) относительно прямой, проходящей через точки A(6, 6), В(3, 4).
4. Даны вершины треугольника A(1, 4), В(-2, 2), С(2, 5). Составить уравнение его высот.
5. Отрезок, ограниченный точками A(-1, 5) и B(5, 8), разделен на три равные части. Определить координаты точек деления.
6. Даны две вершины A(–8, 5) и B(0, 1) треугольника АВС и точка N(-1, 5) пересечения его высот. Составить уравнения сторон этого треугольника.
7. Точка A(–2, 2) является
вершиной квадрата, диагональ которого
лежит на прямой
![]() .
Составить уравнения сторон этого
квадрата.
.
Составить уравнения сторон этого
квадрата.
8. Составить уравнения сторон треугольника
АВС, если даны одна из вершин А(2,
0) и уравнения двух медиан
![]() ,
,
![]() .
.
9. Установить, какие линии определяются следующими уравнениями и построить эти линии.
а)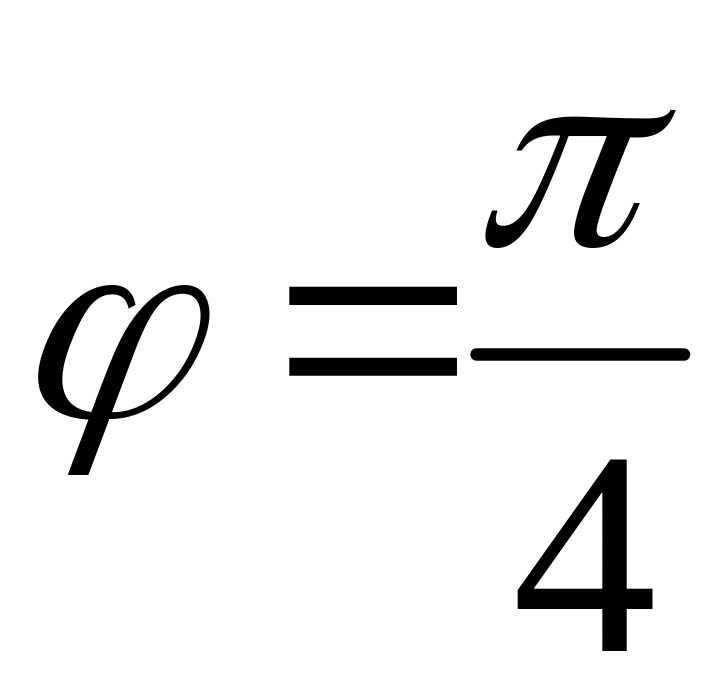 ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() .
.
10. Установить, какая линия определяется
уравнением
![]() .
Найти координаты ее центра, полуоси,
эксцентриситет. Сделать чертеж.
.
Найти координаты ее центра, полуоси,
эксцентриситет. Сделать чертеж.
11. Составить уравнение гиперболы и найти
координаты ее центра и полуоси, если
левая вершина гиперболы находится в
правом фокусе эллипса:
![]() ,
правая вершина гиперболы находится в
вершине параболы
,
правая вершина гиперболы находится в
вершине параболы
![]() ,
эксцентриситет гиперболы равен 4/3
,
эксцентриситет гиперболы равен 4/3![]() .
.
12. Составить уравнение линии, для каждой
точки которой расстояние от точки А(-1,
2) вдвое меньше расстояния от прямой
![]() .
Определить, какая это линия; сделать
чертеж.
.
Определить, какая это линия; сделать
чертеж.
13. Линия задана уравнением
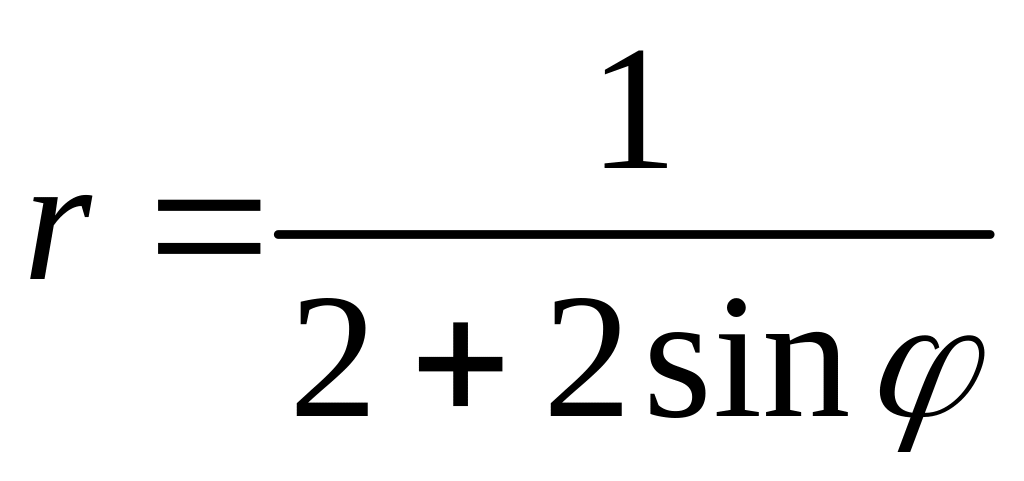 в полярной системе координат.
в полярной системе координат.
Требуется: а) построить линию по точкам,
начиная от
![]() до
до
![]() и придавая
и придавая
![]() значения через промежуток
значения через промежуток
![]() ;
;
б) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
в) по полученному уравнению определить, какая это линия.
14. Вычислить определители:
а) по правилу треугольника;
б) разложением по элементам первой строки;
в) разложением по элементам второго столбца;
г) сведением к треугольному виду:
а)
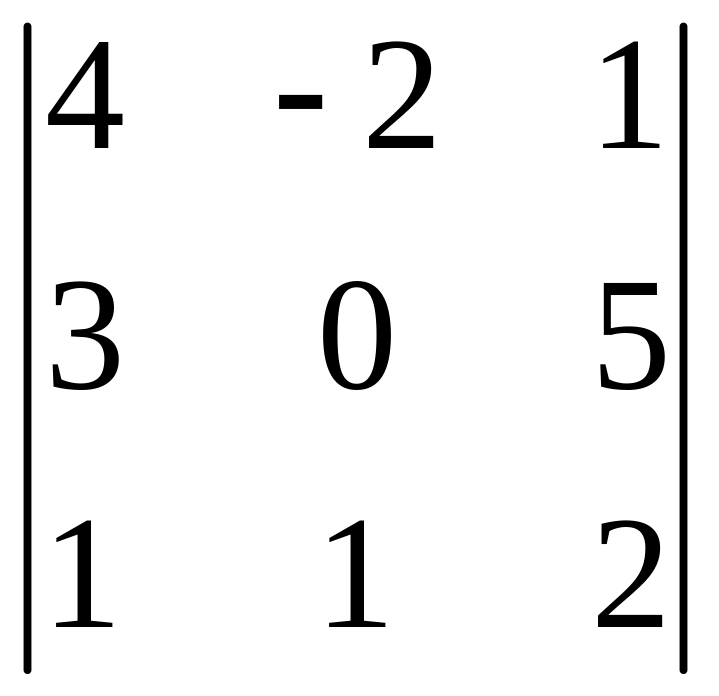 ,
б)
,
б)
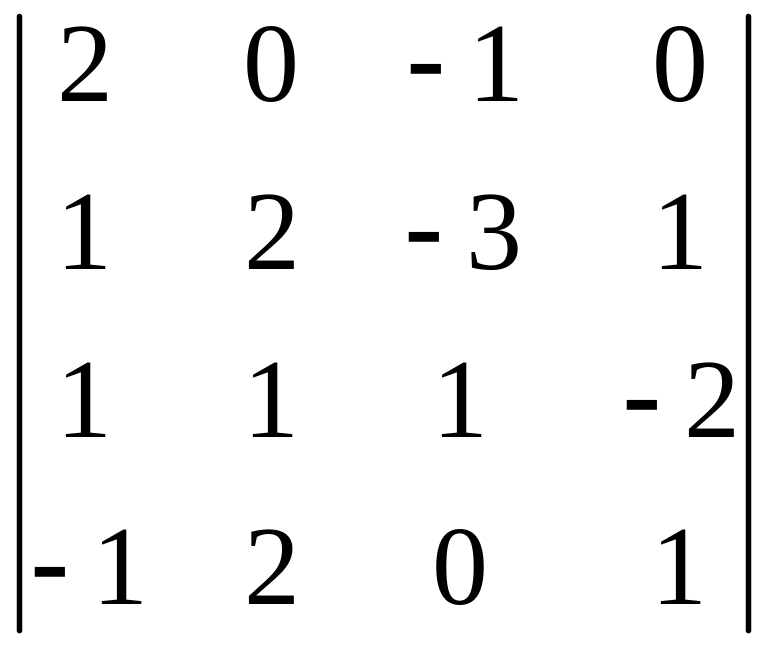 ,
в)
,
в)
 ,
г)
,
г)
 .
.
15. Даны векторы:
![]() 1=(1,
-2, 0);
2=(2,
3, -1);
3=(4,
-3, -1);
1=(1,
-2, 0);
2=(2,
3, -1);
3=(4,
-3, -1);
![]() =(4,
8, -2) в некотором базисе. Показать, что
первые три вектора образуют базис и
найти координаты вектора
в этом базисе.
=(4,
8, -2) в некотором базисе. Показать, что
первые три вектора образуют базис и
найти координаты вектора
в этом базисе.
16. Найти координаты единичного вектора
(орта)
![]() ,
сонаправленного с вектором
,
сонаправленного с вектором
![]() =(1,
-3, 5).
=(1,
-3, 5).
17. Два вектора =(4, -3, 0) и =(-2, 2, 1) приложены к одной точке. Найти координаты:
а) ортов
и
![]() векторов
и
;
векторов
и
;
б) вектора
![]() ;
;
в) вектора
![]() ,
направленного по биссектрисе угла между
векторами
и
при
условии, что
,
направленного по биссектрисе угла между
векторами
и
при
условии, что
![]() .
.
18. Найти проекцию вектора
=(4,
2, 4) на направление вектора
![]() .
.
19. Найти проекцию вектора
![]() на ось, составляющую с координатными
осями
на ось, составляющую с координатными
осями
![]() и
и
![]() углы
углы
![]() ,
а с осью
,
а с осью
![]() тупой угол
тупой угол
![]() .
.
21. Векторы
![]() (2,
-1, 1) и
(2,
-1, 1) и
![]() (1;
0; 2) являются сторонами параллелограмма
ОАСВ. Точка N –
середина стороны ВС. Найти
(1;
0; 2) являются сторонами параллелограмма
ОАСВ. Точка N –
середина стороны ВС. Найти
![]() .
.
22. Вычислить координаты векторного
произведения
![]() и его длину
и его длину
![]() ,
если
=(3,
-2, -1),
,
если
=(3,
-2, -1),
![]() .
.
23. Даны вершины треугольника АВС: А(1, 6, -1), В(4, 4, 5) и С(-2, 1, 7). Найти площадь треугольника и длину высоты, опущенной из вершины А.
24. Вектор
![]() ,
ортогонален к оси
и вектору
,
ортогонален к оси
и вектору
![]() (-1,
2, 3) и образует с осью
острый угол. Найти координаты вектора
(-1,
2, 3) и образует с осью
острый угол. Найти координаты вектора
![]() ,
если
,
если
![]() .
.
25. Найти площадь параллелограмма,
построенного на векторах
![]() и
и
![]() ,
если
,
если
![]() 2,
2,
![]() и
и
![]() .
.
26. Вычислить смешанное произведение
векторов
![]() ,
,
![]() (2,
0, -3),
(2,
0, -3),
![]() (-1,
3, -4).
(-1,
3, -4).
27. Заданы векторы:
![]() ,
,
![]() ,
,
![]() .
Показать, что эти три вектора не
компланарны; установить ориентацию
тройки векторов
.
Показать, что эти три вектора не
компланарны; установить ориентацию
тройки векторов
![]() .
.
28. Вычислить объем пирамиды, вершины которой А(1, 3, 0), В(-1, 6, -6), С(-1, 3, 0), D(1, 6, 2).
39. Вектор
перпендикулярен к векторам
![]() и
и
![]() .
Вычислить
.
Вычислить
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
а тройка векторов
,
а тройка векторов
![]() – левая.
– левая.
30. Составить уравнение плоскости,
проходящей через точку М0(2, -1, 7),
параллельную плоскости
![]() .
.
31. Составить уравнение плоскости,
проходящей через точку М0(5, -3, 0)
и прямую
![]() .
.
32. Составить уравнение плоскости,
проходящей через прямую
![]() перпендикулярно плоскости
перпендикулярно плоскости
![]() .
.
33. Составить уравнение плоскости,
проходящей через точку М0(-1, 2, -4)
перпендикулярно плоскостям
![]() и
и
![]() .
.
34. Найти расстояние от точки М0(-4,
5, 4) до плоскости
![]() .
.
35. Составить канонические уравнения
прямой, проходящей через точку М0(3,
4, -5), параллельно прямой
![]() ,
,
![]() ,
,
![]() .
.
36. Найти координаты точки пересечения
прямой
![]() и плоскости
и плоскости
![]() .
.
37. Найти проекцию точки
![]() на прямую
на прямую
![]() ,
,
![]() ,
,
![]() .
.
38. Найти координаты точки Q,
симметричной точке
![]() относительно плоскости
относительно плоскости
![]() .
.
39. Найти координаты точки Q,
симметричной точке
![]() относительно прямой
относительно прямой
![]() .
.
40. Вычислить растояние от точки
до прямой
![]() .
.
41. Построить эскиз тела, ограниченного поверхностями:
а)
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
,![]() ,
(при
,
(при
![]() )
)
42. Решить систему линейных уравнений методом Гаусса
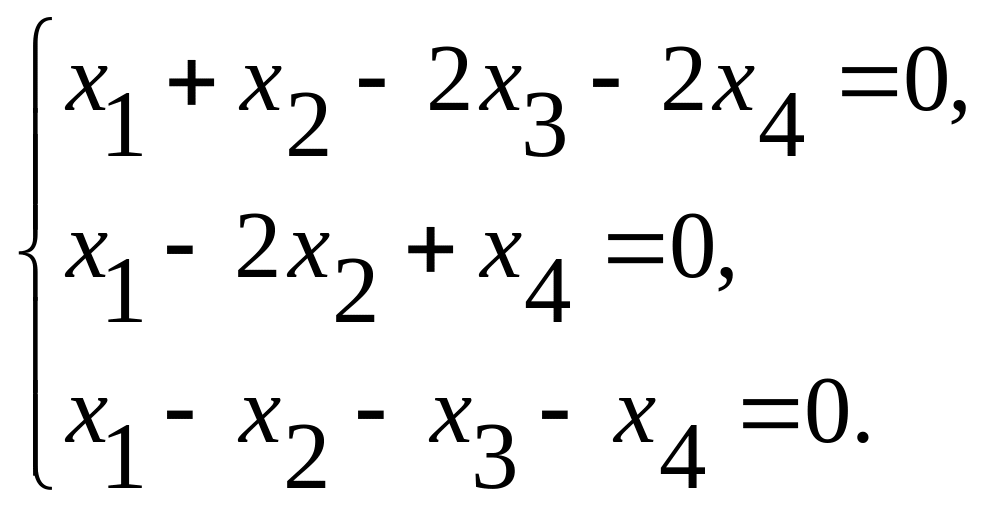
43. Найти матрицу
![]() ,
где
,
где
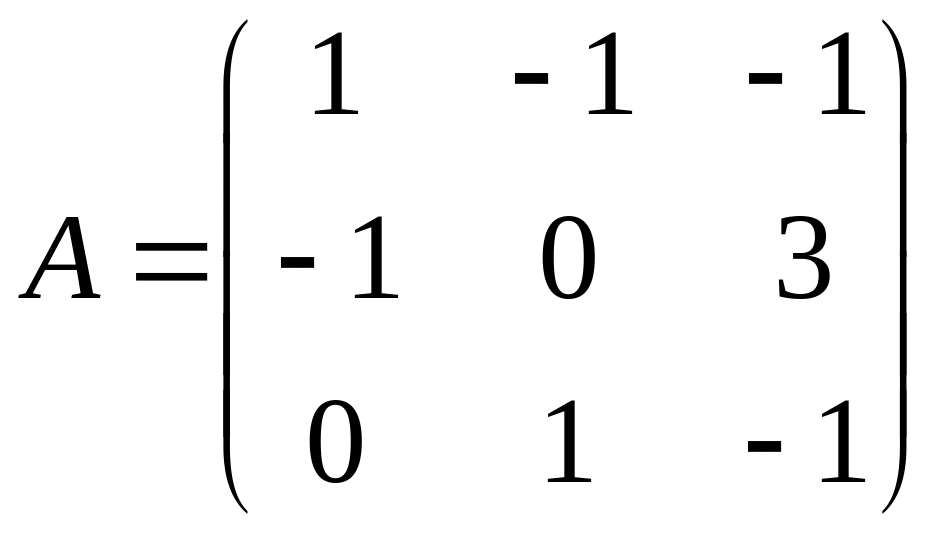 ,
,
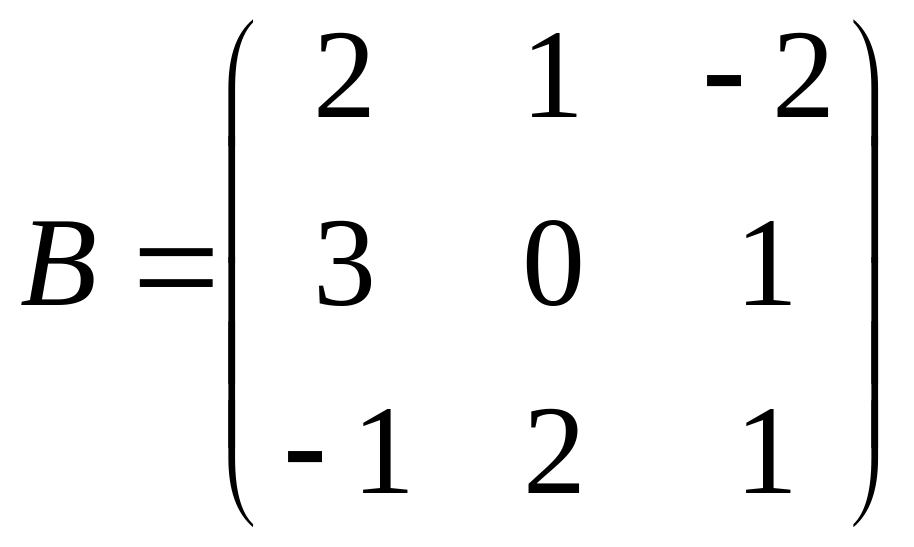 ,
,
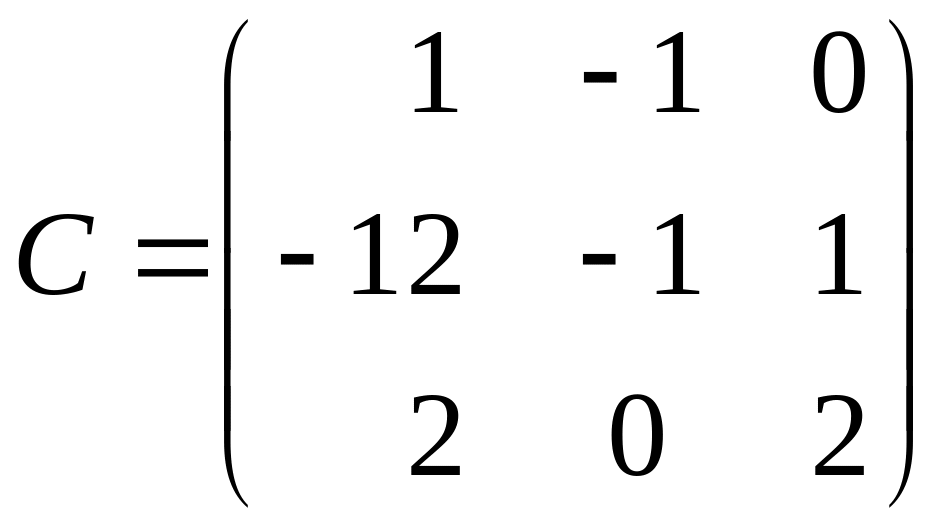 .
.
44. Найти ранг матрицы:
а)
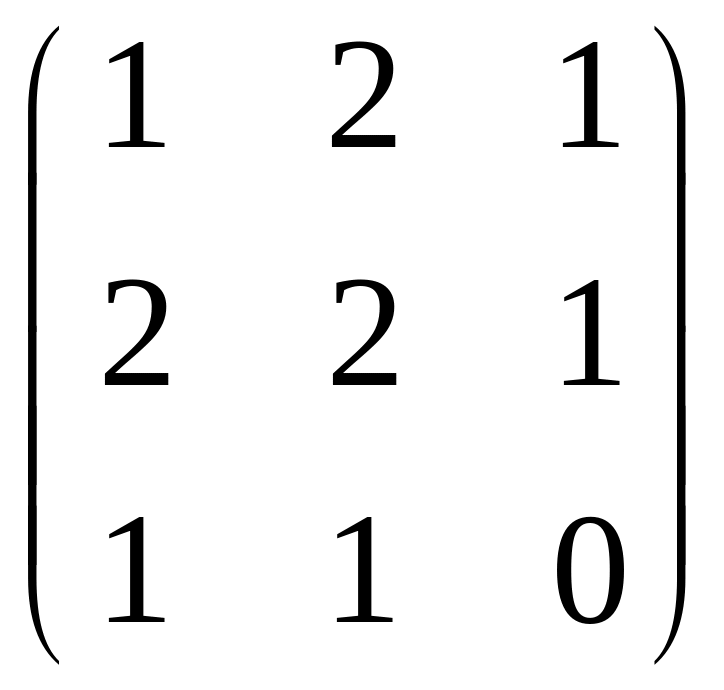 ;
б)
;
б)
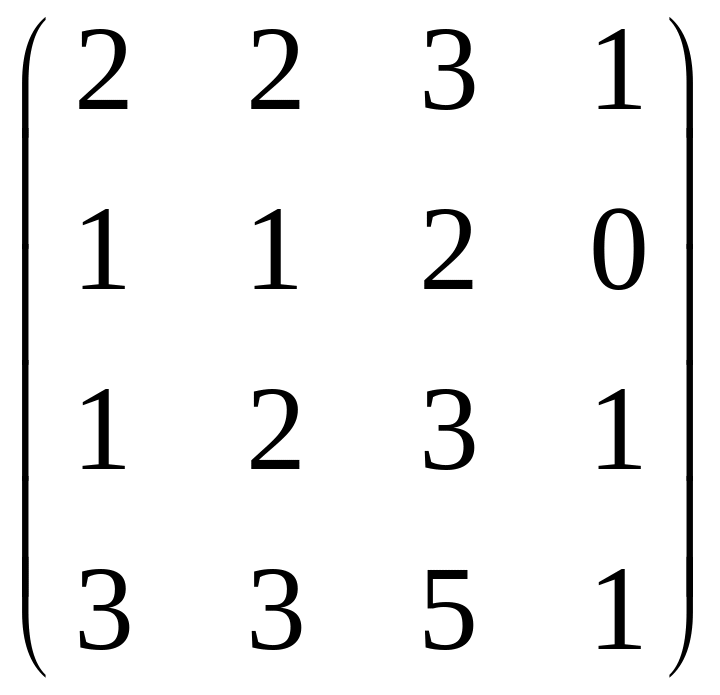 .
.
45. Дана система линейных уравнений
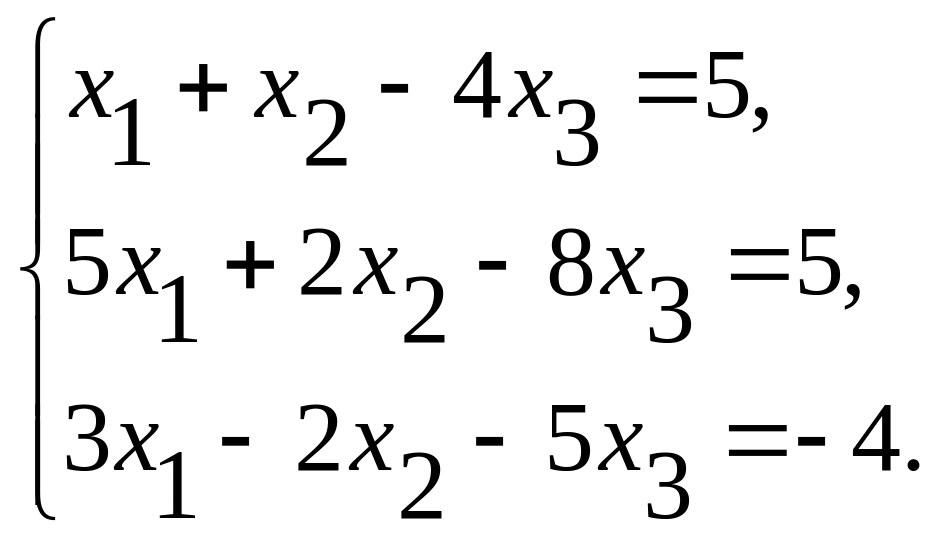
Доказать ее совместность и решить тремя способами:
а) методом Гаусса;
б) средствами матричного исчисления;
в) по формулам Крамера.
46. Является ли вещественным линейным
пространством множество всех вещественных
матриц второго порядка вида
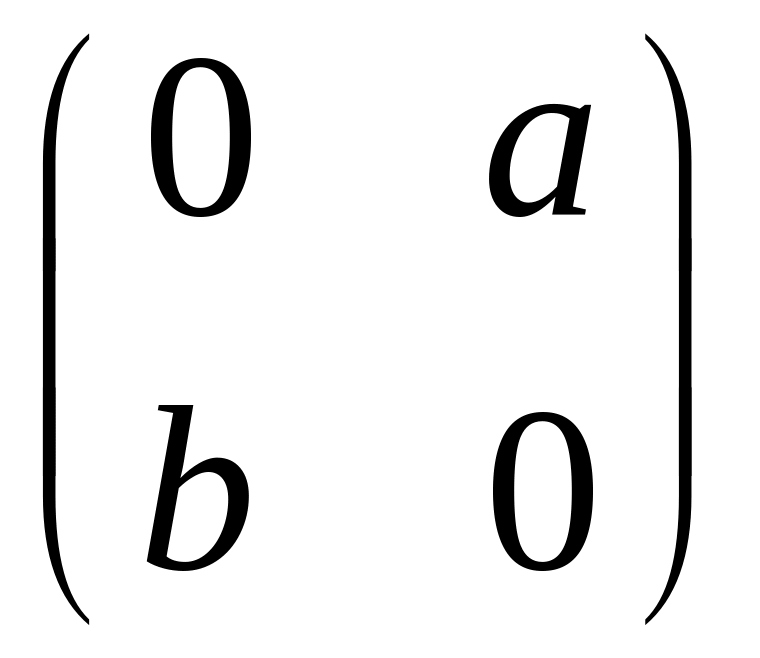 ,
где
,
где
![]() ;
;
47. Выяснить, является ли данная система
векторов из
![]() линейно зависимой?
линейно зависимой?
![]() =(1,
2, 3, -4),
=(1,
2, 3, -4),
![]() =(1,
2, 0, 0),
=(1,
2, 0, 0),
![]() =(1,
-1, -1, 2),
=(1,
-1, -1, 2),
![]() =(2,
1, 2, -2).
=(2,
1, 2, -2).
