
9. Для уравнения в полных дифференциалах

10. Интеграл сходится при

11. Общим решением дифференциального уравнения является

12. Общим решением дифференциального уравнения является

13. Значение решения задачи Коши

14. Уравнениями Бернулли являются

15. Частным решением дифференциального уравнения

16. Частным решением системы

17. Система дифференциальных уравнений может быть сведена к уравнению

1.Верными являются следующие утверждения

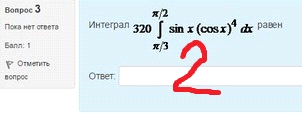
2. Интеграл равен

3.Интеграл равен
4. Формула задает длину дуги кривой

5. Объем тела, образованного при

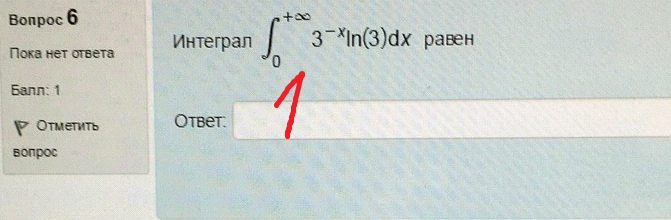
6. Интеграл равен

7. Интеграл равен

8. Интеграл равен

9. Для уравнения в полных дифференциалах

10. Интеграл сходится при

1. Верными являются следующие утверждения

2. Интеграл равен
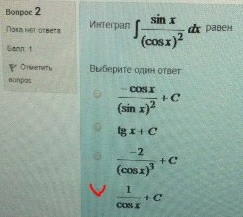
7. Интеграл равен
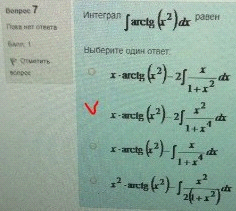
8. Интеграл

9. Для уравнения в полных дифференциалах

10. Интеграл сходится при
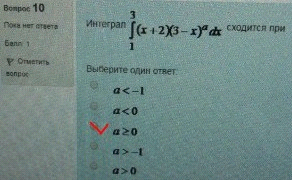
11.Общим интегралом дифференциального уравнения

12. Общим решением дифференциального уравнения является
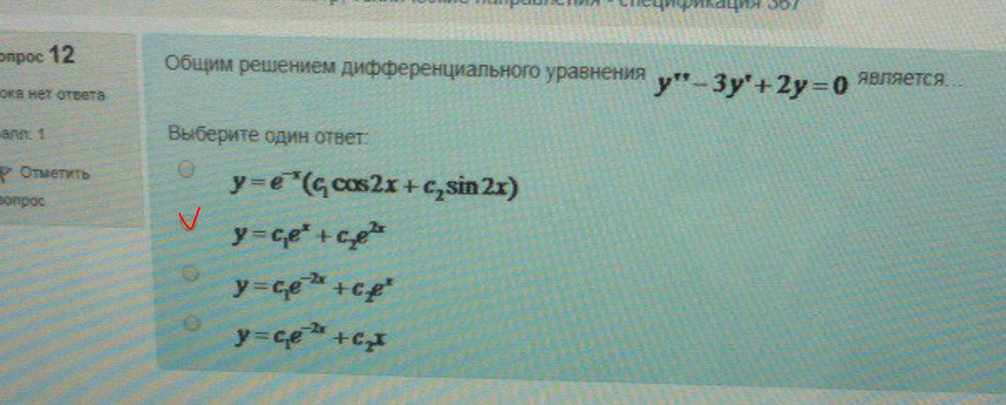
14. Общим решением дифференциального уравнения является
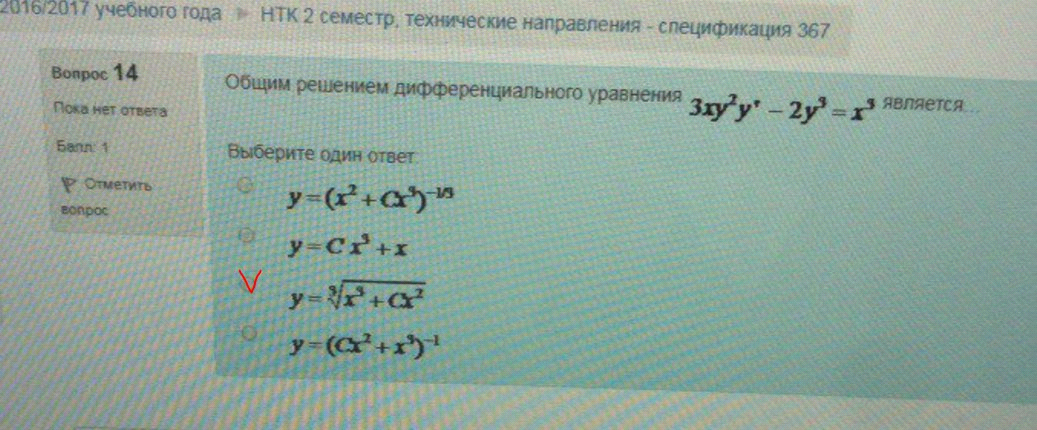
15. Частным решением дифференциального уравнения является
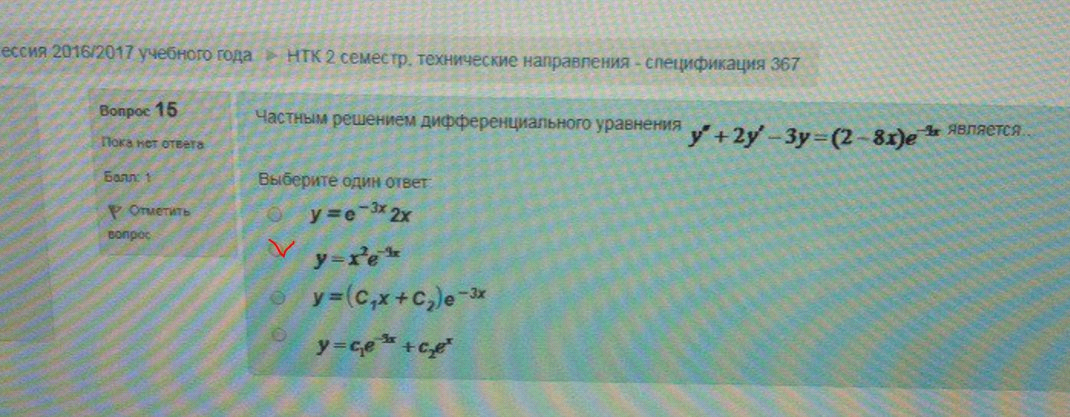
16. Частным решением системы является

1. Верными являются.

2. Интеграл равен
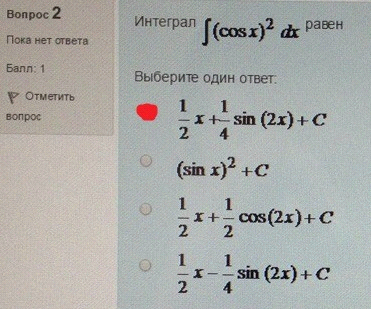
3. Интеграл равен

4. Формула задает длину дуги кривой

5. Объем тела образованного при вращении вокруг оси
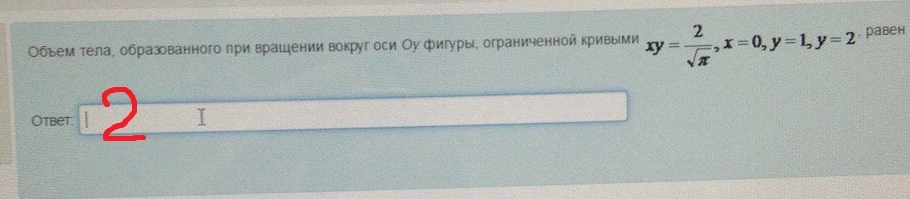
6. Интеграл равен

7. Интеграл равен
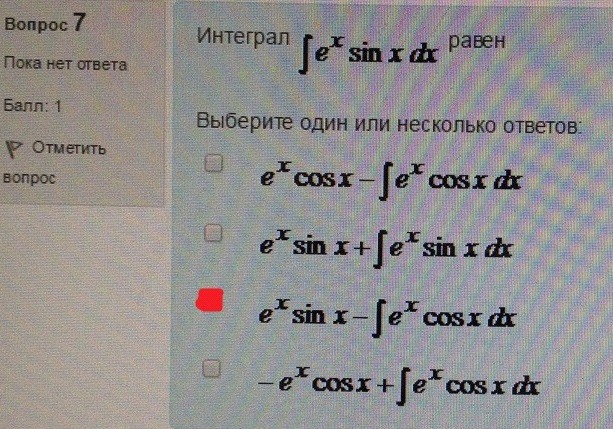
8. Интеграл равен

9. Для уравнения в полных дифференциалах
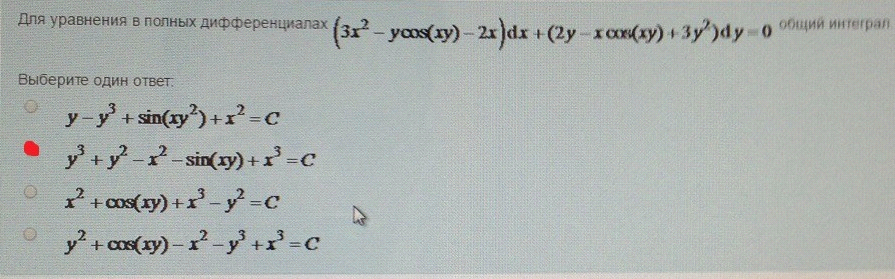
10. Интеграл
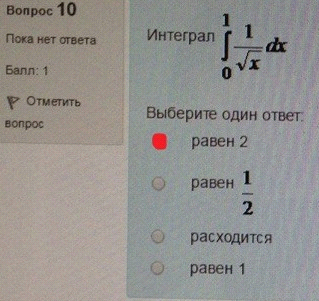
11. Общим решением дифференциального уравнения является

12.Если - общее решение дифференциального уравнения

13,14

15.

16. Частным решением системы является

17. Система Дифференциальных уравнений может быть сведена к уравнению

1. Верными являются следующие утверждения

2.Интеграл равен

3.Интеграл равен

4. Формула задает длину дуги кривой

5. Объем тела, образованного при вращении

6. Интеграл равен
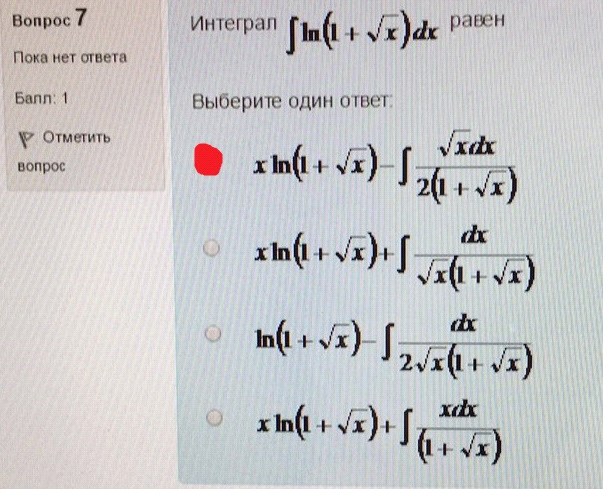
7. Интеграл равен
8. Интеграл равен

9. Для уравнения в полных дифференциалах

10. Интеграл сходится при

11. Общим интегралом дифференциального уравнения

12. Если - общее решение дифференциального

13. Решение дифференциального уравнения первого порядка

14. Уравнениями Бернулли являются

15. Общим решением дифференциального уравнения

16. Частным решением системы является

17. Система дифференциальных уравнений может быть сведена

В

ОТВЕТ 3
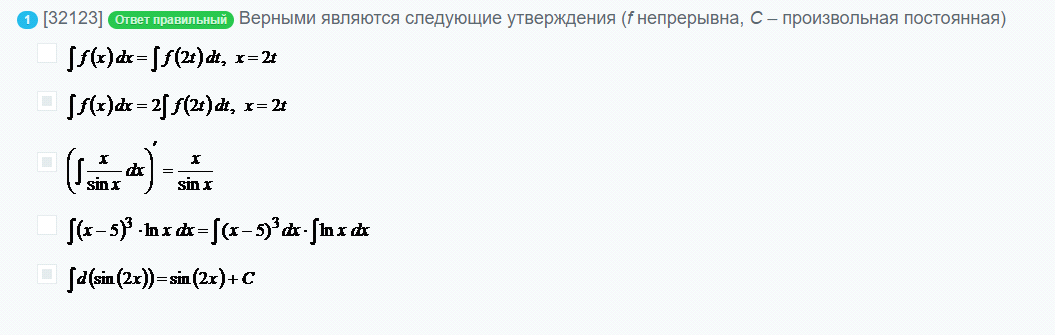
Верными являются следующие утверждения
 ОТВЕТ 2 и 5
ОТВЕТ 2 и 5
 ОТВЕТ 1.2.
ОТВЕТ 1.2.
 ОТВЕТ 1.3.5.
ОТВЕТ 1.3.5.

ОТВЕТ 1.2.5.

ОТВЕТ 1.2.3.
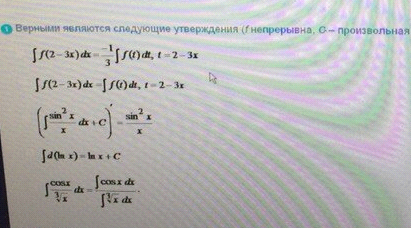 ОТВЕТ 1.3.4.
ОТВЕТ 1.3.4.
Д
Для интегралов полных дифференциалах
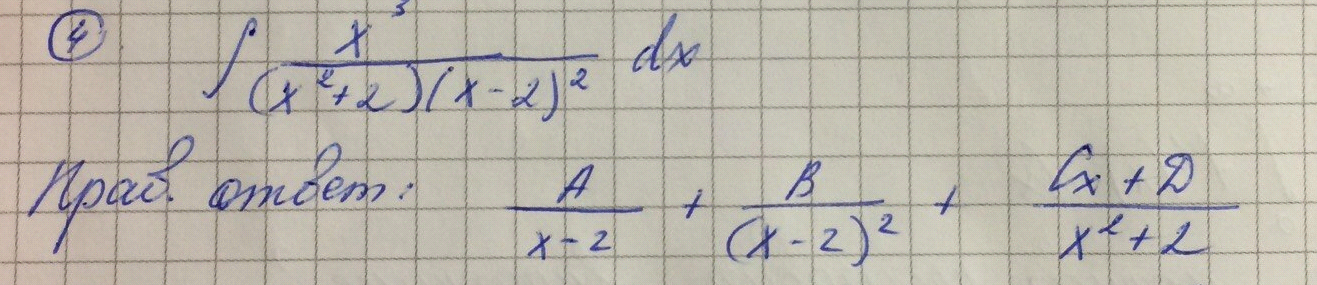
 ОТВЕТ 4
ОТВЕТ 4

ОТВЕТ 4
Для уравнения в полных дифференциалах
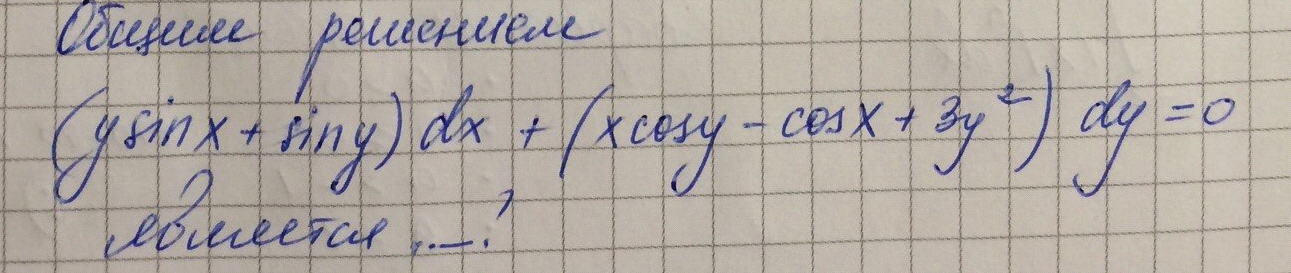
ОТВЕТ –ycosx+xsiny+y^3+C
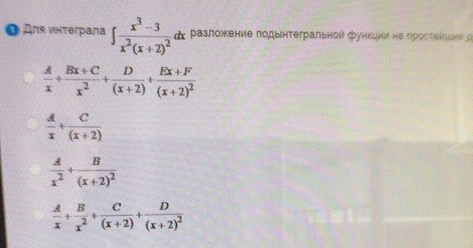 ОТВЕТ
4
ОТВЕТ
4
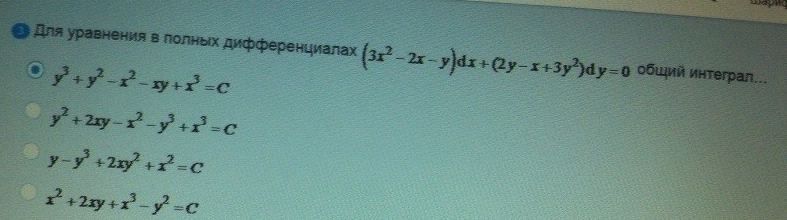
ОТВЕТ 1

ОТВЕТ 2
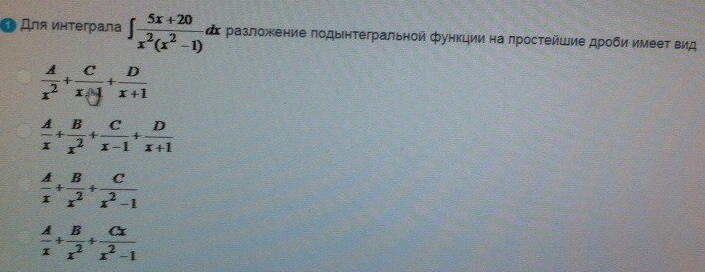
ОТВЕТ 2
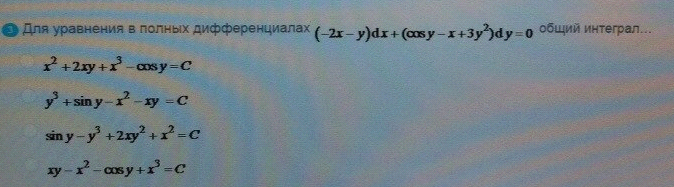
ОТВЕТ 2

ОТВЕТ 1
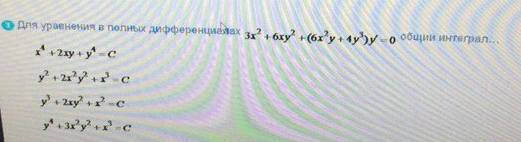
ОТВЕТ 4

ОТВЕТ
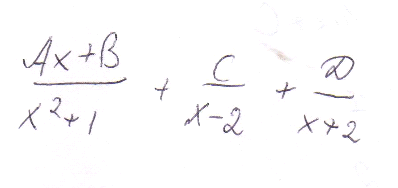

ОТВЕТ 3

Если – общее решение
Если функции
Если производная
 ОТВЕТ 1
ОТВЕТ 1
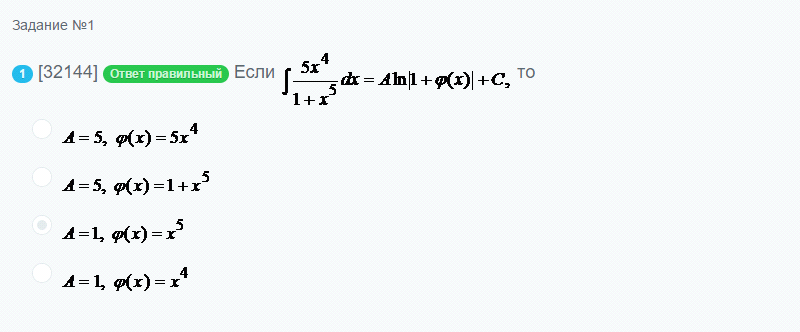

ОТВЕТ 4

ОТВЕТ 3

ОТВЕТ 2

ОТВЕТ 1.4.

ОТВЕТ 1.2.
Значение решения задачи Коши
 ОТВЕТ
1
ОТВЕТ
1
 ОТВЕТ 1
ОТВЕТ 1
 ОТВЕТ 2
ОТВЕТ 2
 ОТВЕТ -1
ОТВЕТ -1
Интеграл

ОТВЕТ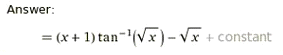
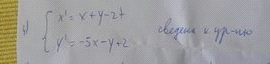
ОТВЕТ: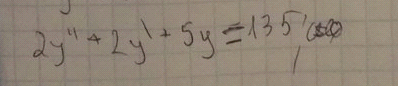
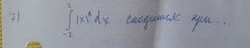 ОТВЕТ
n<1
ОТВЕТ
n<1
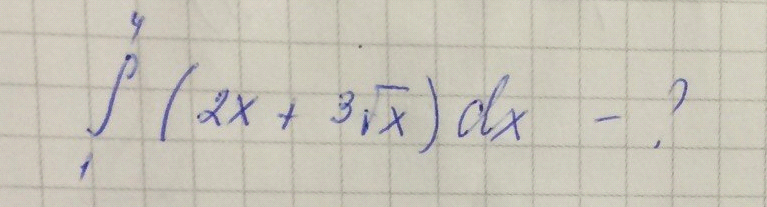 ОТВЕТ =29
ОТВЕТ =29
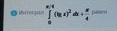 ОТВЕТ
=1
ОТВЕТ
=1
 ОТВЕТ
а> -1
ОТВЕТ
а> -1
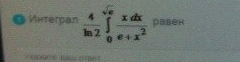 ОТВЕТ: 2
ОТВЕТ: 2
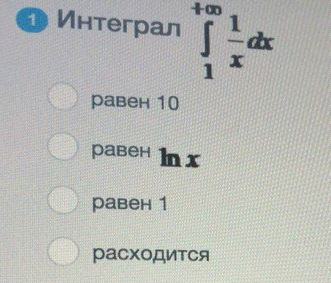 ОТВЕТ 4
ОТВЕТ 4
 ОТВЕТ: 4
ОТВЕТ: 4
 ОТВЕТ
ОТВЕТ

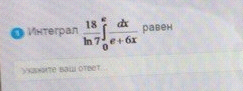 ОТВЕТ 3
ОТВЕТ 3
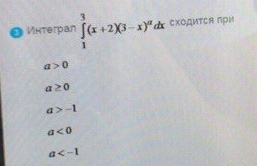 ОТВЕТ 2
ОТВЕТ 2
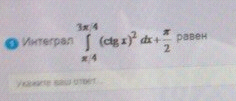 ОТВЕТ 2
ОТВЕТ 2
 ОТВЕТ 1
ОТВЕТ 1
 ОТВЕТ 3
ОТВЕТ 3
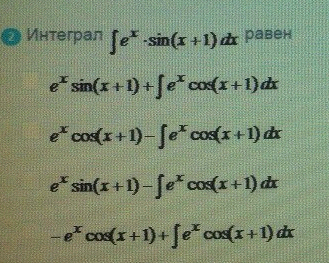 ОТВЕТ 4
ОТВЕТ 4
 ОТВЕТ 1
ОТВЕТ 1
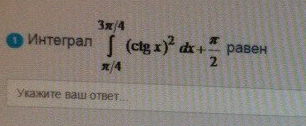 ОТВЕТ 2
ОТВЕТ 2
 ОТВЕТ 3 и ???
ОТВЕТ 3 и ???
 ОТВЕТ 5
ОТВЕТ 5
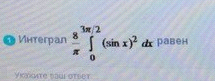 ОТВЕТ 6
ОТВЕТ 6
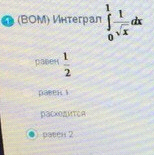 ОТВЕТ 4
ОТВЕТ 4
 ОТВЕТ 76
ОТВЕТ 76
 ОТВЕТ 3
ОТВЕТ 3
 ОТВЕТ 3
ОТВЕТ 3
 ОТВЕТ 3
ОТВЕТ 3
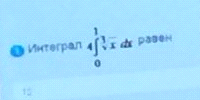 ОТВЕТ 3
ОТВЕТ 3
 ОТВЕТ 2
ОТВЕТ 2
 ОТВЕТ 5
ОТВЕТ 5
 ОТВЕТ 3 и 1
ОТВЕТ 3 и 1
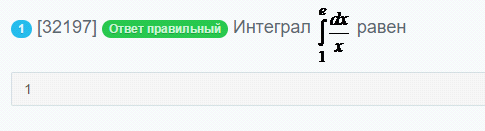



Несобственный интеграл расходится
 ОТВЕТ 2
ОТВЕТ 2
Определить с помощью
Объем тела, образованного при
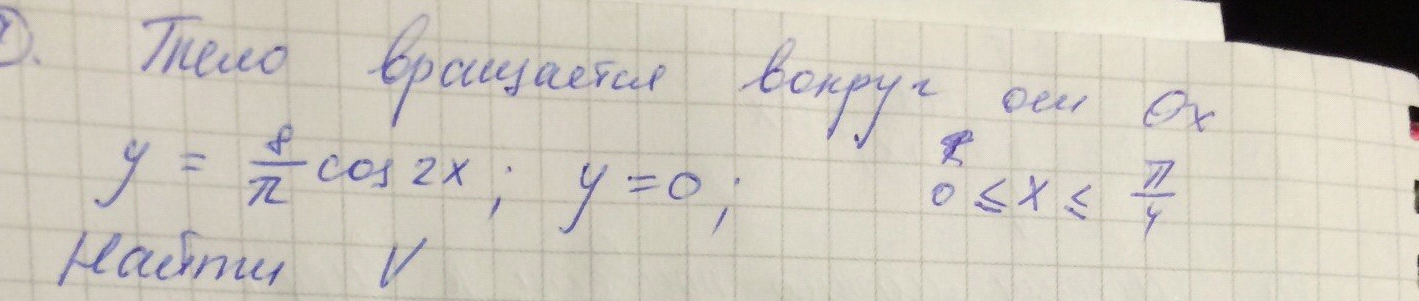
ОТВЕТ 4 или 8 (???)
 ОТВЕТ 8
ОТВЕТ 8
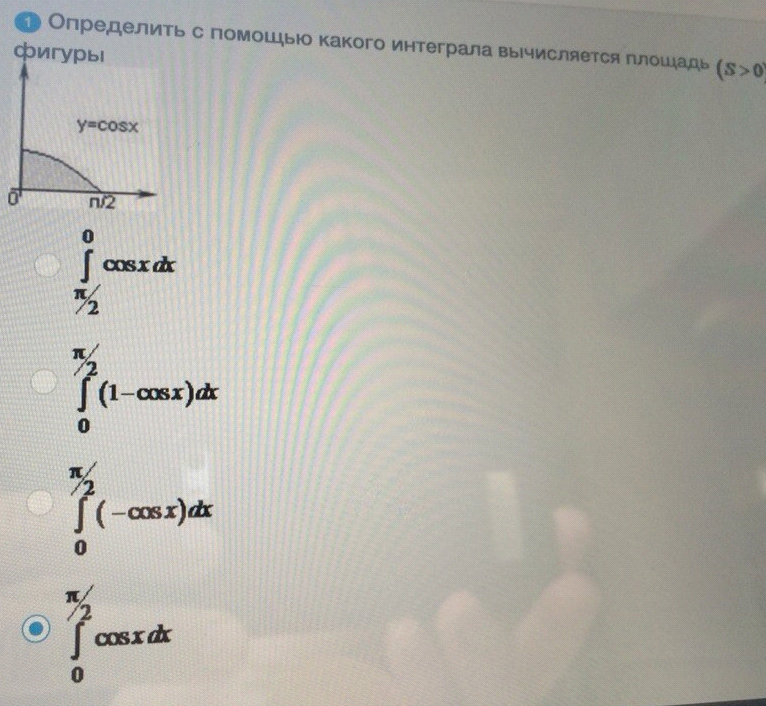 ОТВЕТ 4
ОТВЕТ 4
 ОТВЕТ 4
ОТВЕТ 4
 ОТВЕТ 1.2.
ОТВЕТ 1.2.

ОТВЕТ 2
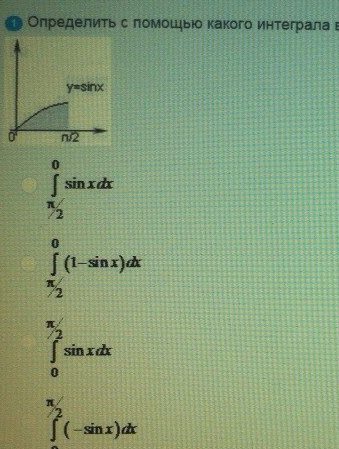 ОТВЕТ 3
ОТВЕТ 3

ОТВЕТ 2

ОТВЕТ 3
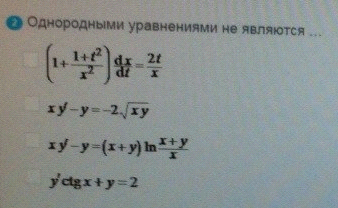 ОТВЕТ 1.4.
ОТВЕТ 1.4.

ОТВЕТ 2

ОТВЕТ 1
 ОТВЕТ 1.3.
ОТВЕТ 1.3.

ОТВЕТ 2

ОТВЕТ4

ОТВЕТ 1

ОТВЕТ 2

ОТВЕТ 2
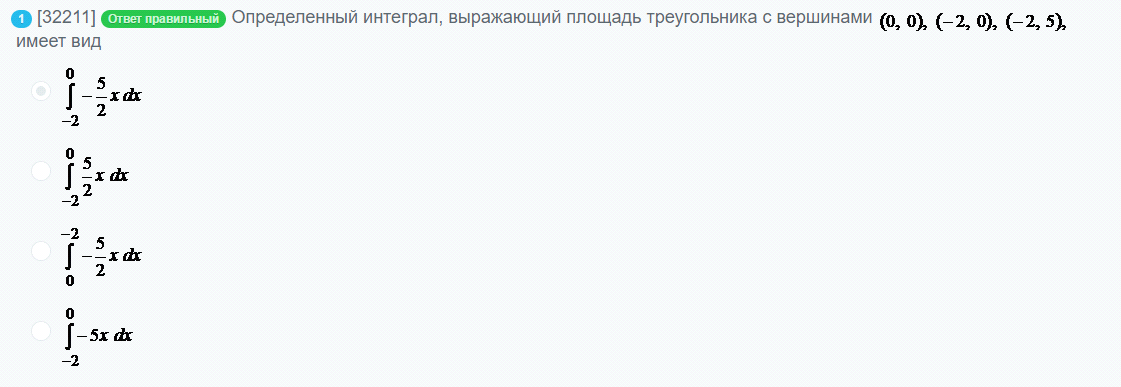
После введения функции
 ОТВЕТ 1
ОТВЕТ 1
 ОТВЕТ 1
ОТВЕТ 1
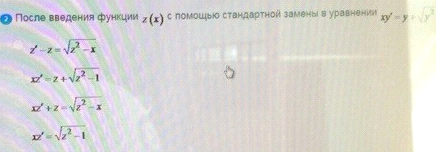 ОТВЕТ 4
ОТВЕТ 4
Система дифференциальных уравнений
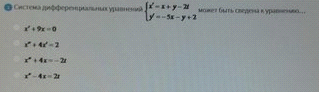
ОТВЕТ 3
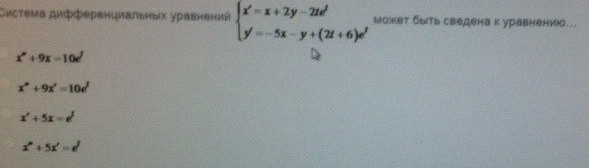 ОТВЕТ 1
ОТВЕТ 1
 ОТВЕТ 2
ОТВЕТ 2
 ОТВЕТ 4
ОТВЕТ 4
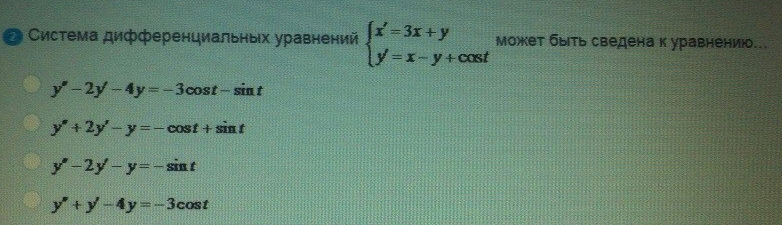
ОТВЕТ 1
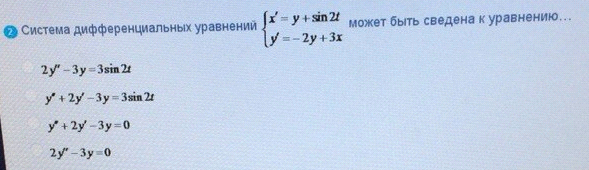
ОТВЕТ 2
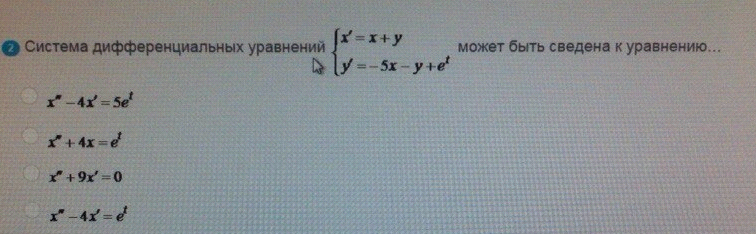
ОТВЕТ 2
Фундаментальную систему решений однородного
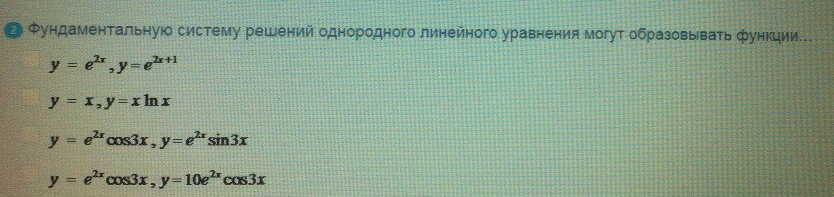
ОТВЕТ 2.3.
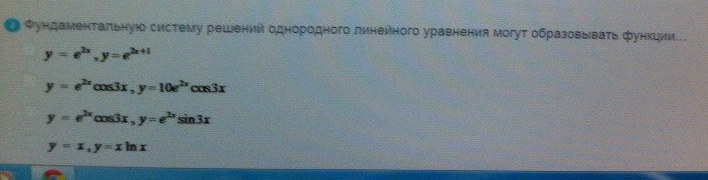
ОТВЕТ 3.4.

ОТВЕТ 4

НЕВОШЕДШЕЕ
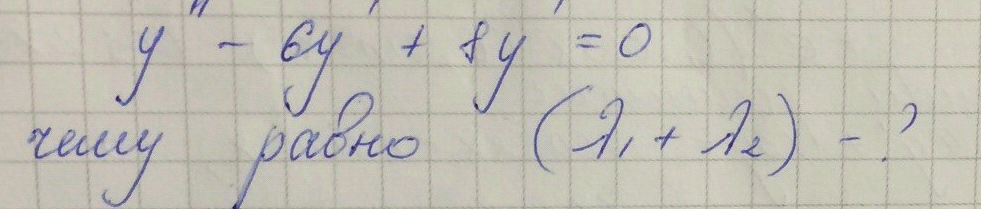 ОТВЕТ
-2
ОТВЕТ
-2
Как можно представить интеграл (2 вариант ответа)

Значение решения задачи Коши
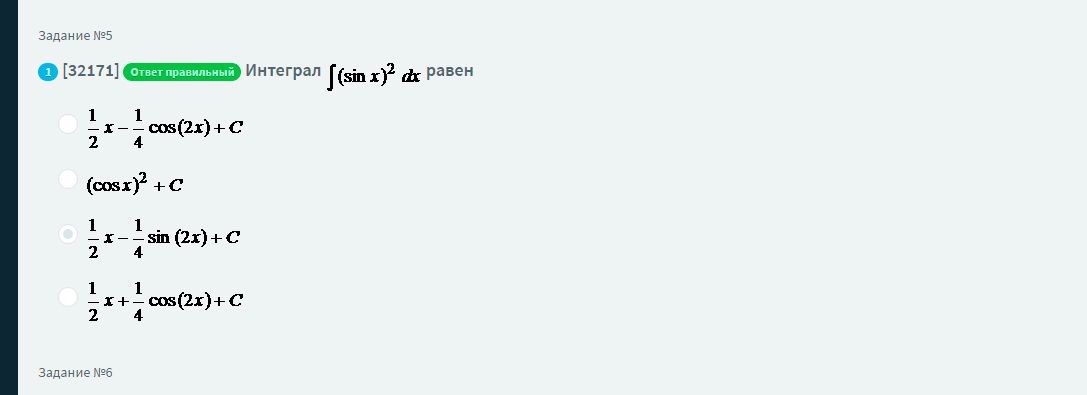
 Интеграл
равен
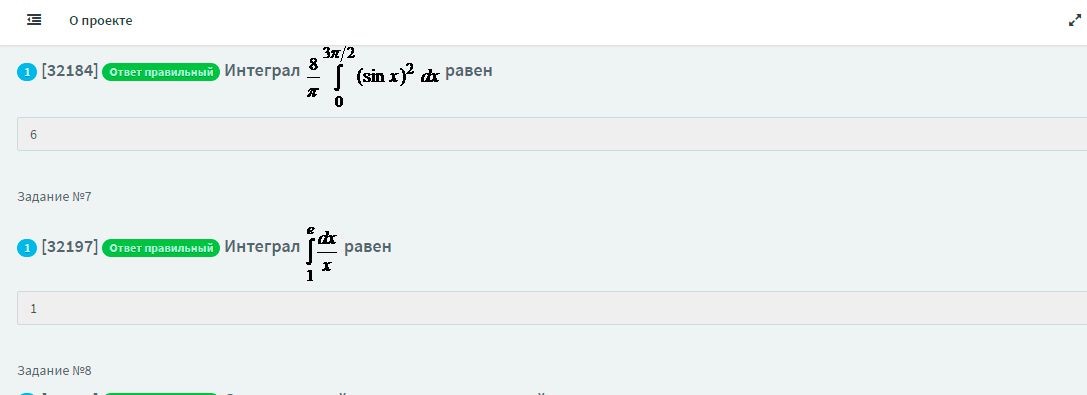
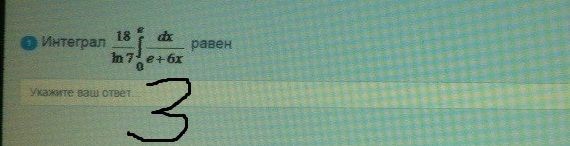
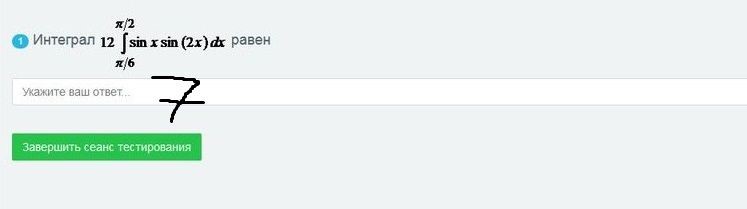
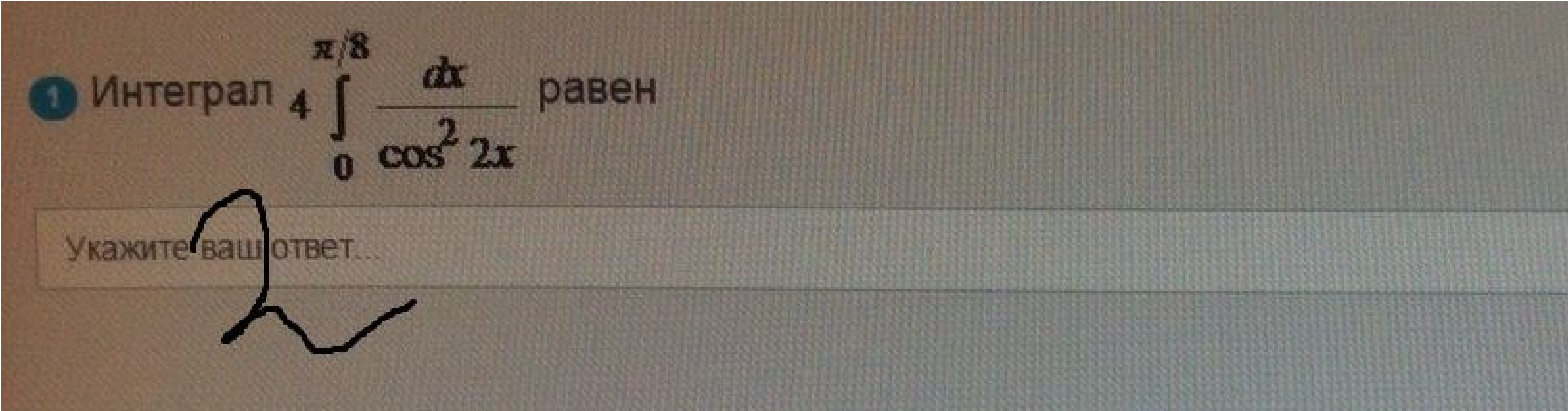
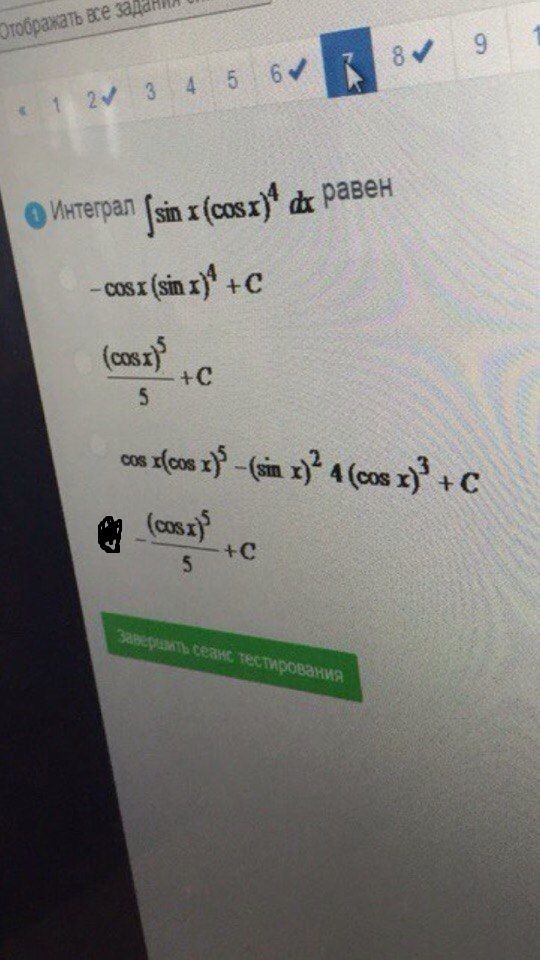
Интеграл
равен
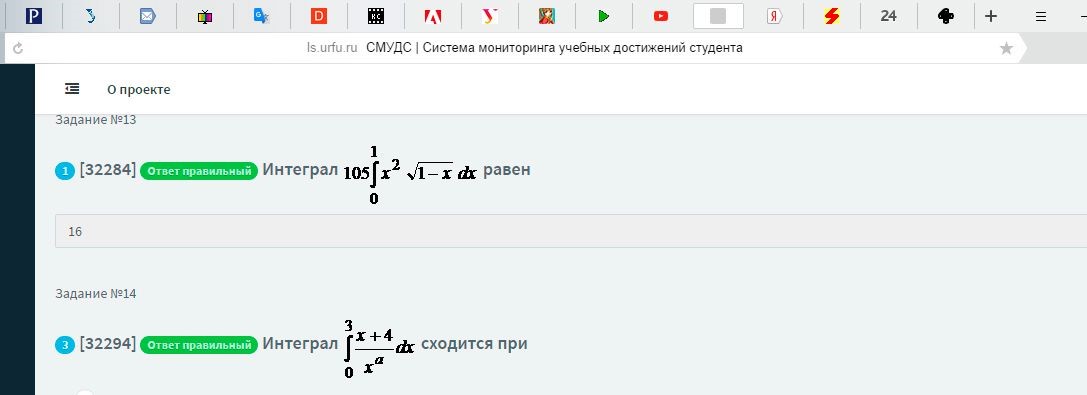

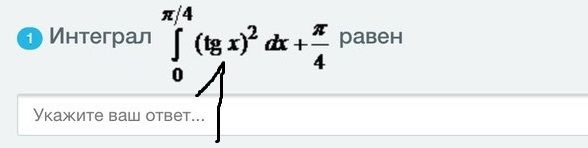


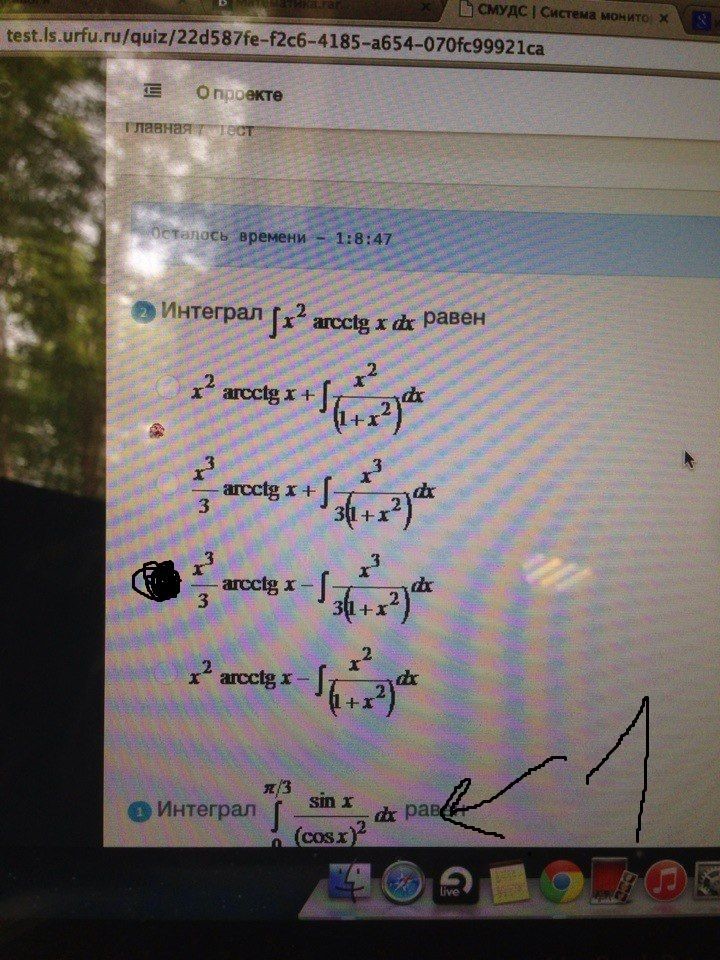

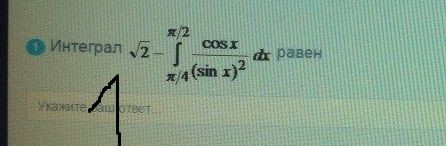


Интеграл сходится при

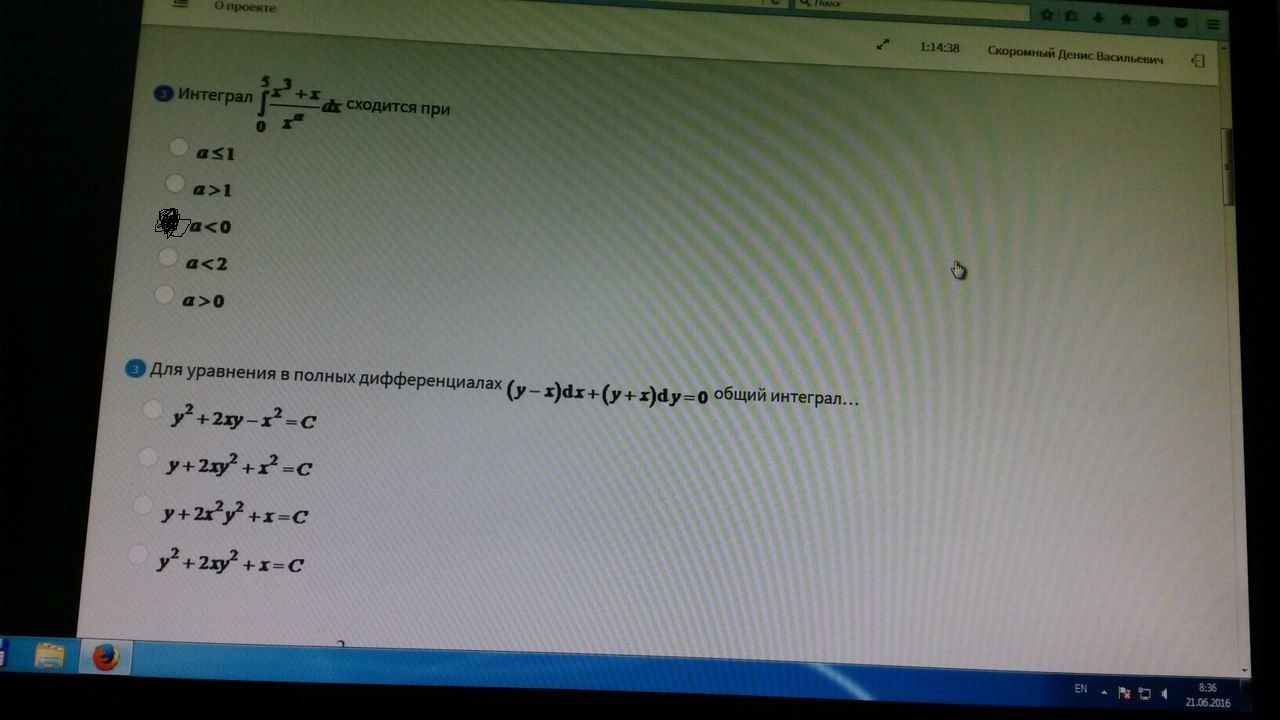


Объем тела, образованного при вращении вокруг оси


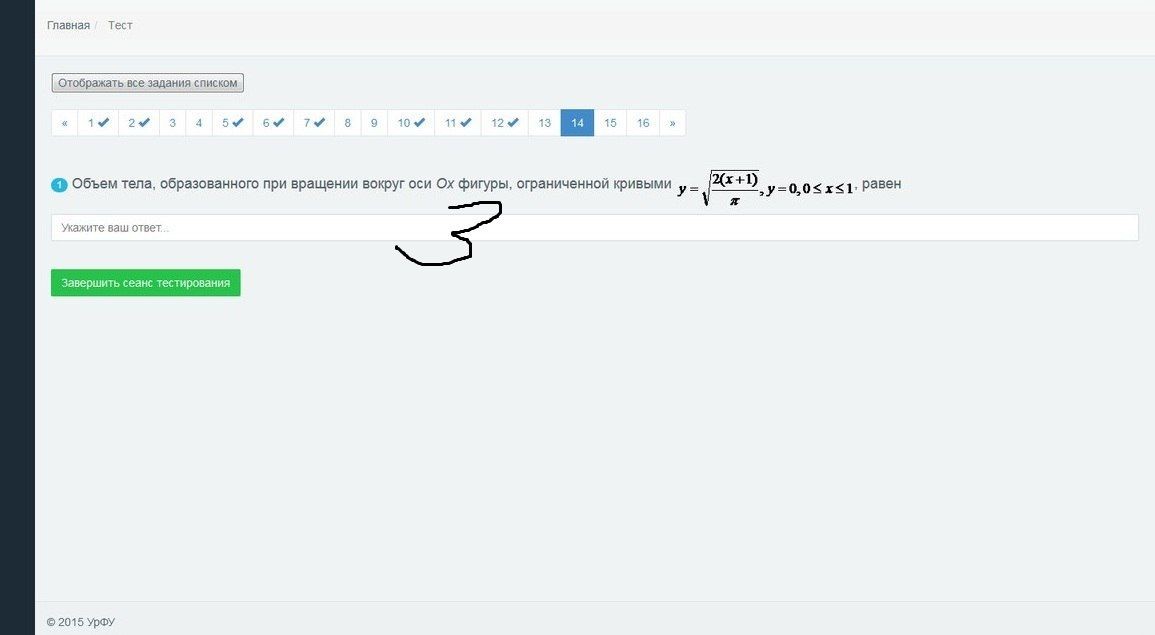

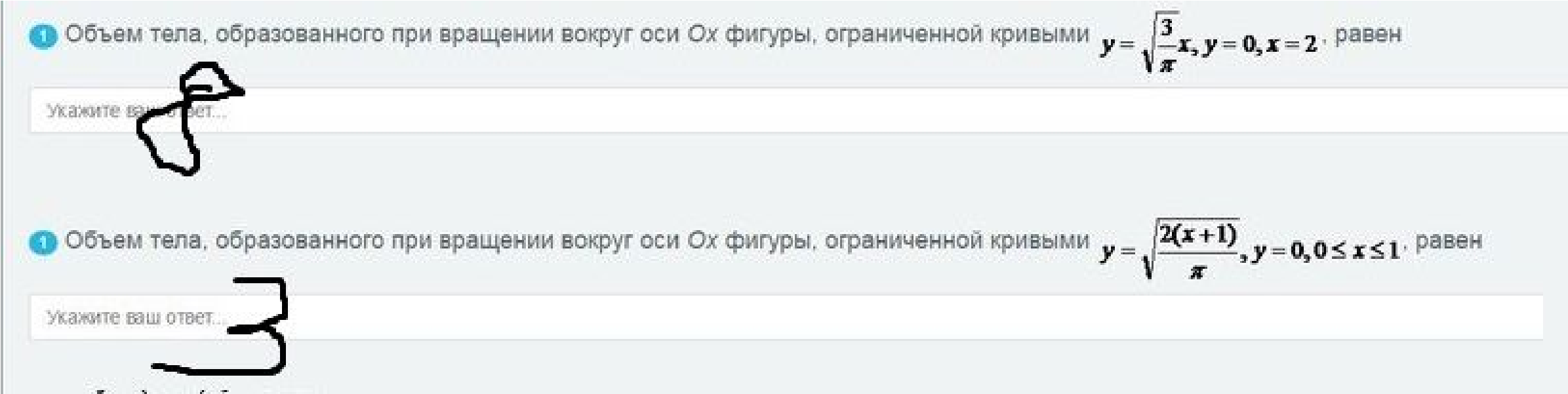
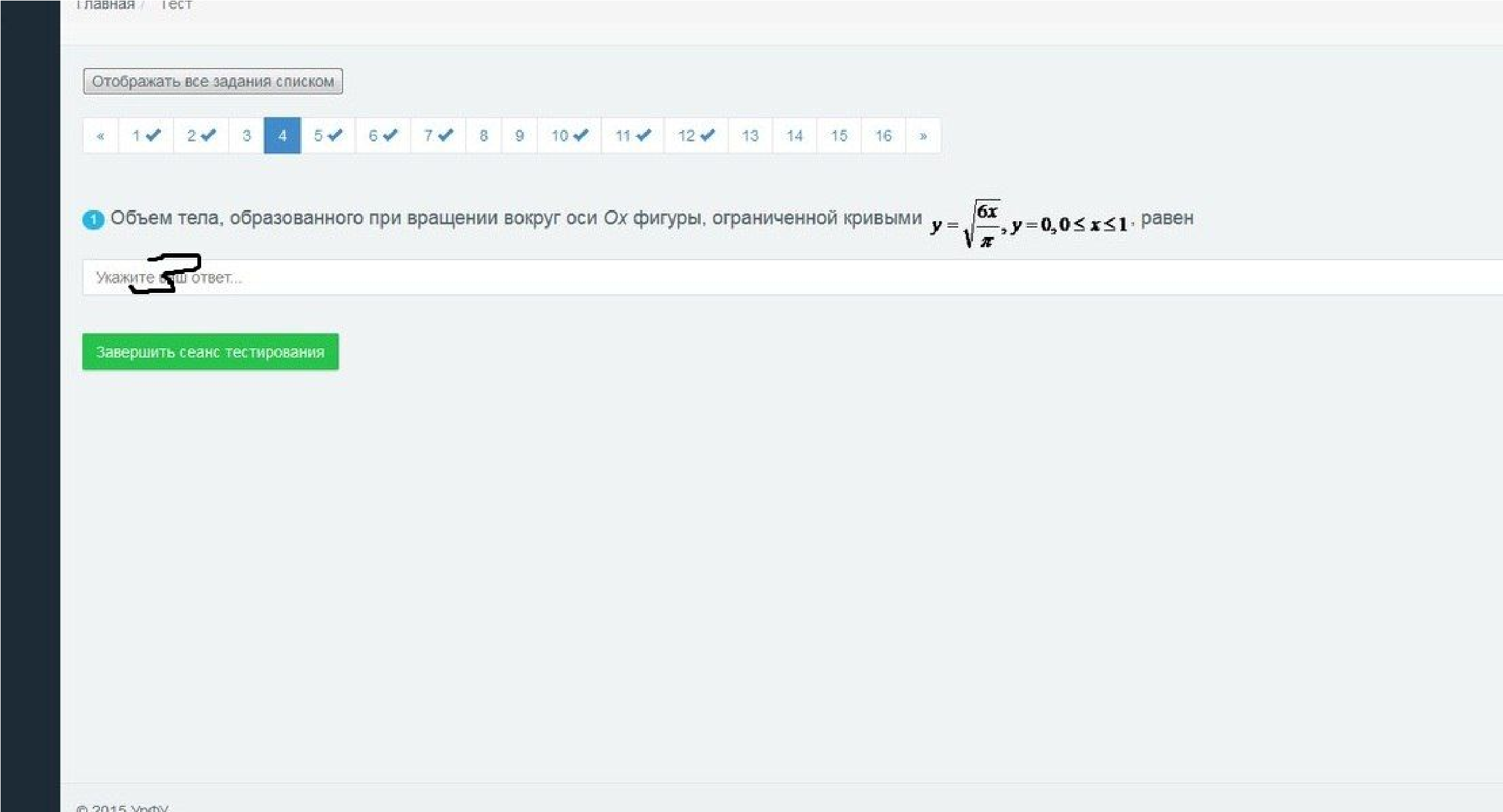

Если





Вариант 1
если
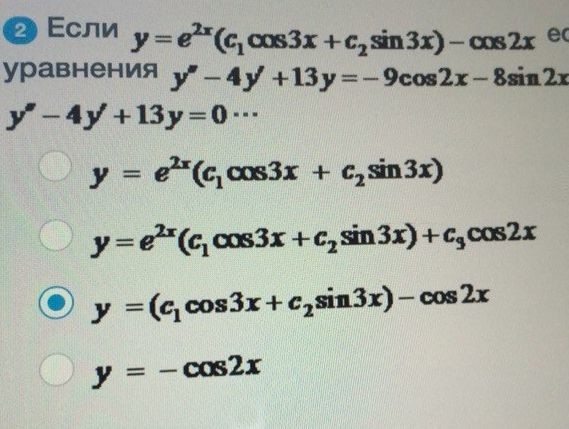 ОТВЕТ
1
ОТВЕТ
1
интеграл
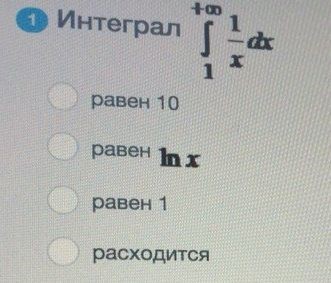 ОТВЕТ
РАСХОДИТСЯ
ОТВЕТ
РАСХОДИТСЯ
Интеграл сходится при
 ОТВЕТ :
3
ОТВЕТ :
3
Если – общее решение дифференциального

ОТВЕТ 4
Для интеграла разложение подынтегральной функции
 ОТВЕТ
4
ОТВЕТ
4
значение решения задачи Коши
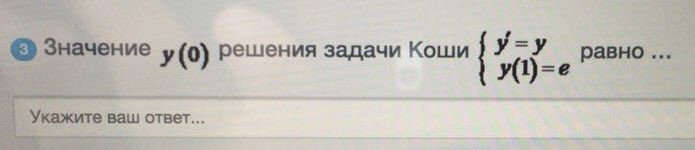 ОТВЕТ
1
ОТВЕТ
1
Объем тела, образованного при вращении вокруг
 ОТВЕТ
8
ОТВЕТ
8
Система дифференциальных уравнений
 ОТВЕТ
2
ОТВЕТ
2
Верными являются следующие утверждения
 ОТВЕТ
1.2.
ОТВЕТ
1.2.
Определить с помощью какого интеграла
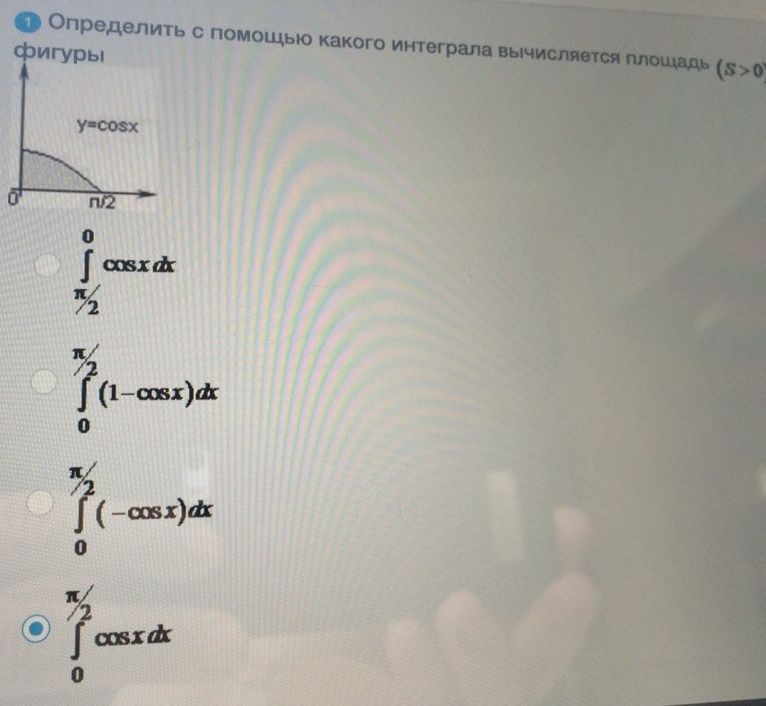 ОТВЕТ
4
ОТВЕТ
4
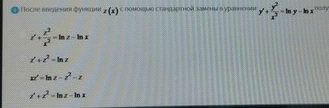
После введения функции с помощью
 ОТВЕТ
1
ОТВЕТ
1
Вариант 2
Система линейных дифференциальных уравнений
 ОТВЕТ
4
ОТВЕТ
4
После введения функции с помощью стандартной замены
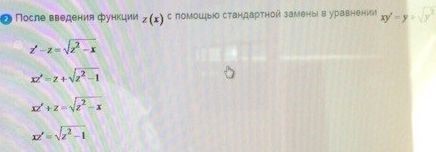 ОТВЕТ
4
ОТВЕТ
4
Верными являются следующие утверждения
 ОТВЕТ
1.3.5.
ОТВЕТ
1.3.5.
если – общее решение дифференциального уравнения

ОТВЕТ 3
Определить с помощью какого интеграла вычисляется площадь
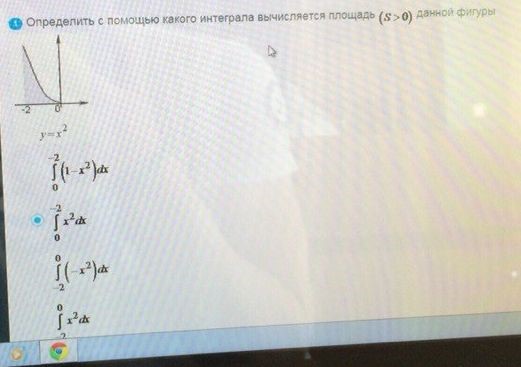 ОТВЕТ
4
ОТВЕТ
4
Если функции образуют
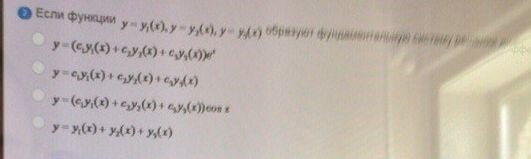
ОТВЕТ 2
Для уравнения в полных дифференциалах

ОТВЕТ 4
интеграл равен

ОТВЕТ 3
Для интеграла разложение подынтегральной функции
 ОТВЕТ
4
ОТВЕТ
4
интеграл равен
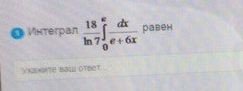 ОТВЕТ
3
ОТВЕТ
3
интеграл сходится при
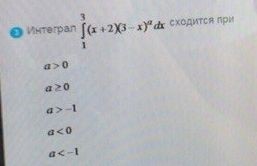 ОТВЕТ
2
ОТВЕТ
2
интеграл равен
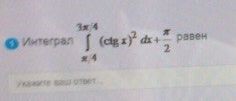 ОТВЕТ
2
ОТВЕТ
2
Несобственный интеграл расходится если
 ОТВЕТ
1
ОТВЕТ
1
Вариант 3
Однородными уравнениями не являются
 ОТВЕТ
1.2.
ОТВЕТ
1.2.
Фундаментальную систему решений однородного линейного уравнения
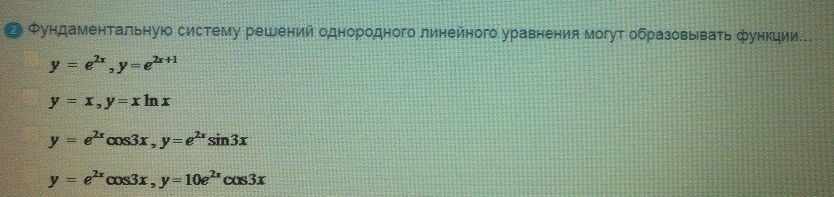
ОТВЕТ 2.3.
Для уравнения в полных дифференциалах

ОТВЕТ 1
интеграл сходится при
 ОТВЕТ
4
ОТВЕТ
4
значение решения задачи Коши
 ОТВЕТ
2
ОТВЕТ
2
интеграл равен
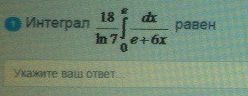 ОВТЕТ
3
ОВТЕТ
3
Объем тела, образованного при вращении

ОТВЕТ 2
Система дифференциальных уравнений
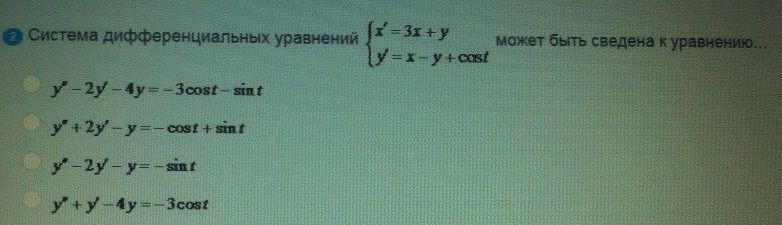
ОТВЕТ 1
интеграл равен
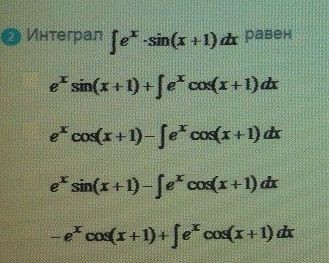 ОТВЕТ
3,4
ОТВЕТ
3,4
Определить с помощью какого интеграла
 ОТВЕТ
3
ОТВЕТ
3
Верными являются следующие утверждения

оТВЕТ 1.2.5.
для интеграла разложение подынтегральной функции
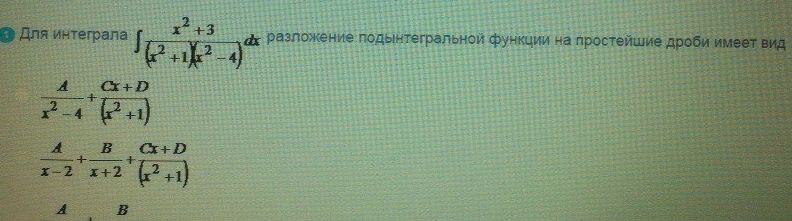
ОТВЕТ 2
Общим решением дифференциального уравнения

ОТВЕТ 2
интеграл равен
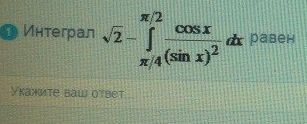 ОТВЕТ
1
ОТВЕТ
1
Если производная непрерывна на

ОТВЕТ 1.4.
Вариант 4
интеграл равен
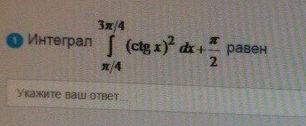 ОТВЕТ
2
ОТВЕТ
2
Для интеграла разложение подынтегральной функции
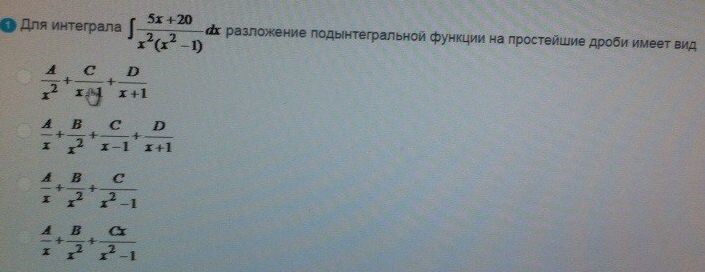
ОТВЕТ 2
Верными являются следующие утверждения

ОТВЕТ 1.2.3.
Для уравнения в полных дифференциалах

ОТВЕТ 2
Общим решением дифференциального уравнения

ОТВЕТ 3
Однородными уравнениями не являются
 ОТВЕТ
1.4.
ОТВЕТ
1.4.
Фундаментальную систему решений однородного линейного

ОТВЕТ 3.4.
интеграл равен
 ОТВЕТ
3…..
ОТВЕТ
3…..
интеграл сходится при
 ОТВЕТ
5
ОТВЕТ
5
Определить с помощью какого интеграла вычисляется

ОТВЕТ 2
Если производная непрерывна на

ОТВЕТ 1.2.
Объем тела, образованного при вращении

ОТВЕТ 1
