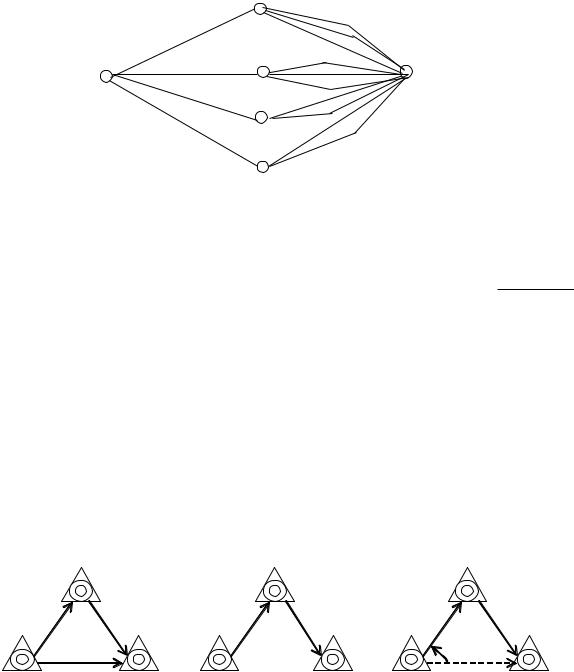
Вероятностный граф по исходящей связи приведен на рис. 11.5.

А

ИШК

Рис. 11.5. Вероятностный граф по исходящей связи Потери по исходящей связи:

Тема 12. Метод расчета сети с обходными направлениями

12.1. Принцип построения сети с обходными направлениями

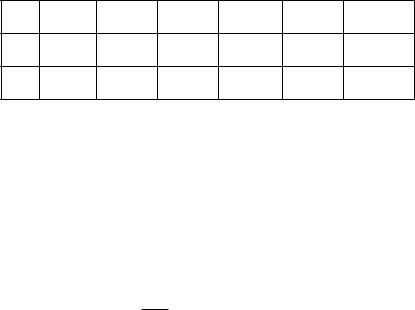
Идею построения сети с обходными направлениями можно пояснить на следующем простом примере. Рассмотрим АТСi , АТС j , АТСк (рис.12.1).

Рис. 12.1. Возможные схемы обслуживания нагрузки Yij :

47

kij , kik , kkj – капитальные зарплаты на 1 кан.-км линейных сооружений на направлениях ij, ik, kj соответственно;

– капитальные затраты на один вход коммутационного оборудования на АТС i, j и k соответственно.

Капитальные затраты на одну линию в направлении ij рассчитываются следующим образом:

Kij kij lij kвхj .

Аналогично рассчитываются капитальные затраты на одну линию Кik и Кkj.

ij и ikj, при котором обеспечивались бы минимальные суммарные капитальные затраты на линейные сооружения и станционное оборудование при заданном качестве обслуживания.

Если станция АТСi имеет возможность выбора обходного направления, то

не обслуженная линиями прямого направления, автоматически передается на направление, состоящее из двух участков: ik и kj. Эту нагрузку называют избыточной. Направление, на которое поступает избыточная нагрузка, называют обходным.

Расчет сети с обходными направлениями в общем случае сводится к решению двух задач:

- определяется такое число линий на прямых направлениях, чтобы суммарные затраты на построение сети были минимальными;

- рассчитывается такое число линий на обходных направлениях, чтобы обеспечивалось заданное качество обслуживания потоков вызовов.

48

Основная трудность решения поставленных задач заключается в расчете числа линий в обходных направлениях. Дело в том, что поток вызовов, создающий избыточную нагрузку, не является простейшим, а имеет ярко выраженный «пиковый» характер.

Распределение вероятностей избыточного потока вызовов описывается не распределением Пуассона, а отрицательным биноминальным распределением. При прочих равных условиях для обслуживания избыточного потока необходимо иметь больше линий, чем для обслуживания простейшего потока.

12.2. Определение оптимального числа линий в прямом направлении

Оптимальное число линий в прямом направлении зависит от

отношения затрат на одну линию в прямом направлении к затратам на одну

рассчитывается число линий в обходном направлении – Pобх.

1)экономия от уменьшения числа линий в прямом направлении на одну от оптимального не превышает затрат на организацию дополнительного числа линий в обходном направлении, необходимых для обслуживания дополнительной нагрузки, поступающей на обходное направление при уменьшении числа линий в прямом направлении на одну;

2)затраты на организацию дополнительной линии в прямом направлении больше экономии от соответствующего уменьшения числа линий на обходном направлении.

При полнодоступном неблокируемом включении линий МСЭ-Т рекомендует (Рекомендация Е.522) использовать следующее условие оптимальности:

где EV *ij (Аij ) - первая формула Эрланга; М – увеличение пропускной

способности пучка линий обходного направления при добавлении к этому пучку одной линии.

Поэтому для подбора можно воспользоваться приближенным методом определения Vij* . Как показали исследования, зависимость Vij* f (Аij ) при

прямой

При этом на обходное направление будет передаваться интенсивность нагрузки mij = Aij E13,13 ( )=10∙0,084339 = 0,84 Эрл.

Таблица 12.1. Значения коэффициентов а и в для расчёта числа линий

12.3. Метод расчёта числа линий (каналов) при обслуживании вызовов избыточной нагрузки

Для характеристики избыточной нагрузки используют два параметра:

Для простейшего потока вызовов значение Zij 1 , для избыточного

потока Zij>1.

Математическое ожидание и дисперсию избыточной нагрузки можно найти из следующих выражений:

В общем случае на обходное направление могут поступать избыточные нагрузки от нескольких прямых направлений. Если принять, что поступающие на прямые направления нагрузки являются независимыми, то избыточные нагрузки будут также независимыми и параметры объединенной на обходном направлении нагрузки определяются из выражения:

обх – интенсивность нагрузки, создаваемой простейшим потоком вызовов и поступающей на обходное направление. Этой нагрузки может и не

быть, это зависит от схемы организации связи.

Определить число линий в обходном направлении можно с помощью метода Вилкинсона, являющегося одним из вариантов метода эквивалентных замен.

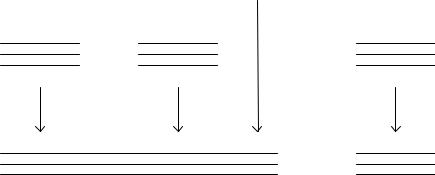
Сущность метода заключается в замене схемы включения рис. 12.2а на схему рис.12.2б, называемую эквивалентной схемой. В эквивалентной

эквивалентные по пропускной способности линий на обходном направлении.

Рис.12.2. Реальная и эквивалентная схемы включения линий на обходном направлении

решая систему уравнений методом подбора:

51

можно воспользоваться приближенными выражениями, полученными шведским учёным Раппом:

Порядок расчета линий в обходном направлении методом Вилкинсона следующий:

1)при известных Aij и ε по (12.2) рассчитывается V*.

2)по (12.3) для каждого прямого направления ij рассчитываются

mij и dij;

3) по (12.4) определяются значения математического ожидания и дисперсии избыточных нагрузок, не обслуженных в прямых

6) рассчитывается Pэкв. = mпот. /Aэкв.;

7) с помощью таблиц Пальма по значениям Pэкв и Aэкв

определяется S V обх ;

8) рассчитывается число линий в обходном направлении

52