Лабы / Лабораторная работа №33

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра теории электрических цепей

Лабораторная работа №33

по дисциплине

Теоретические основы электротехники

на тему

Исследование активных интегрирующих и дифференцирующих цепей

Проверил: к.т.н Мосичев А. В.

Москва, 2023

Цель работы: c помощью машинного эксперимента получить форму напряжения на выходе активных интегрирующих и дифференцирующих цепей при различных формах напряжения на входе. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.

Исходные данные:

Входное напряжение

K₁ = 10, K₂ = 6, C = 100 нФ, R = 1 кОм;

u₁(t) = U_m  – синусоидальное входное напряжение, где

U_m = 1 В – амплитуда входного напряжения;

f = 2 кГц – частота входного напряжения;

t   [0; 1] мс – время.

u₁(t) – прямоугольное входное напряжение;

VZERO = -1 – минимальное значение, В;

VONE = 1 – максимальное значение, В;

P1 = 0 – начало переднего фронта, с;

P2 = 0 – начало плоской вершины импульса, с;

P3 = 0.25e-3 – конец плоской вершины импульса, с;

P4 = 0.25e-3 – момент достижения уровня VZERO, с;

P5 = 0.5e-3 – период следования импульсов, с.

u₁(t) – треугольное входное напряжение (рис. );

VZERO = -1, VONE = 1, P1 = 0, P2 = 0, P3 = 0.25e-3, P4 = 0.25e-3, P5 = 0.5e-3.

Для интегрирующей цепи

u₂(t) = K₁  , где

u₂(t) – выходное напряжение;

К₁ – коэффициент пропорциональности.

Для активной интегрирующей цепи

Для дифференцирующей цепи

u₂(t) = K₂  , где

u₂(t) – выходное напряжение;

К₂ – коэффициент пропорциональности.

Для активной дифференцирующей цепи

U₂ =   U₁

Предварительный расчёт

1. Для интегрирующей цепи

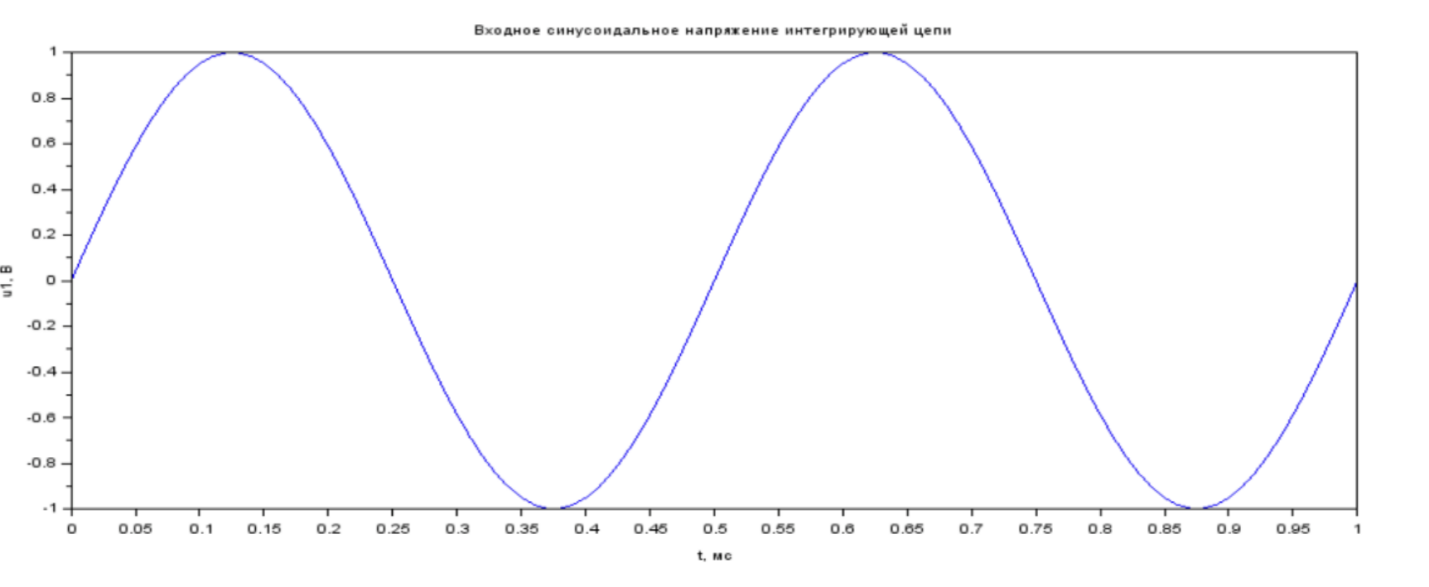
Рис. 1.1 График входного синусоидального напряжения интегрирующей цепи

Рис. 1.2 График выходного синусоидального напряжения интегрирующей цепи

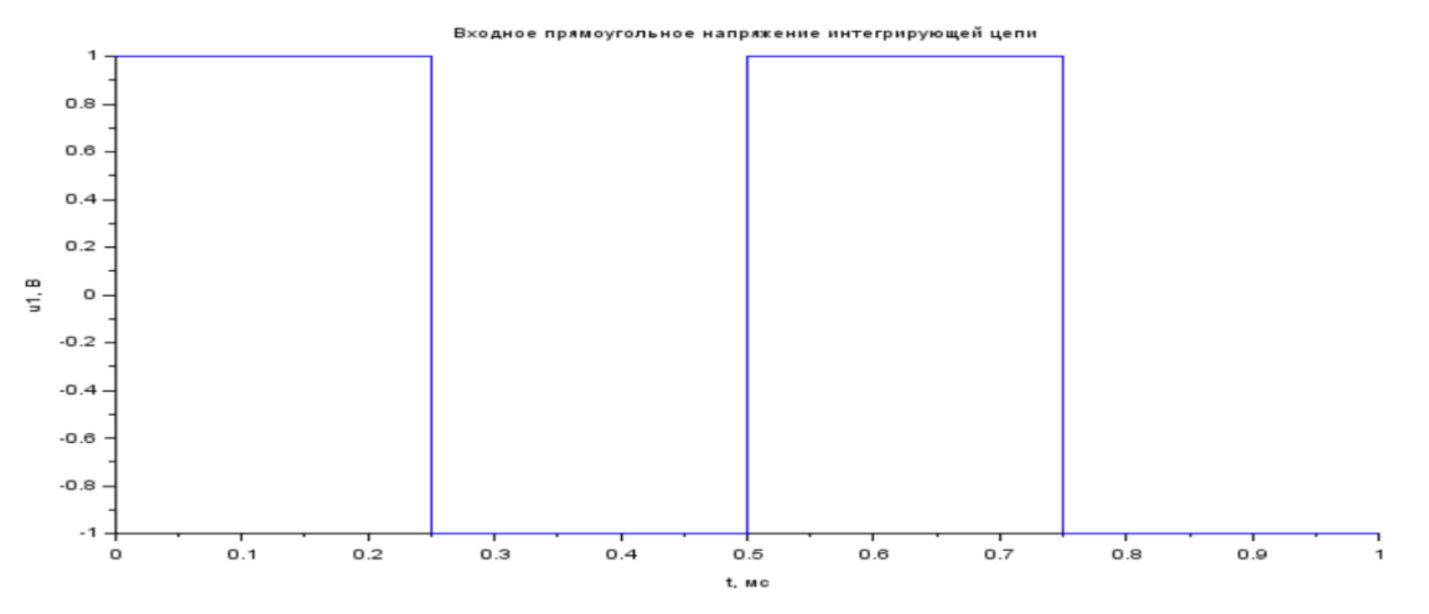
Рис. 1.3 График входного прямоугольного напряжения интегрирующей цепи

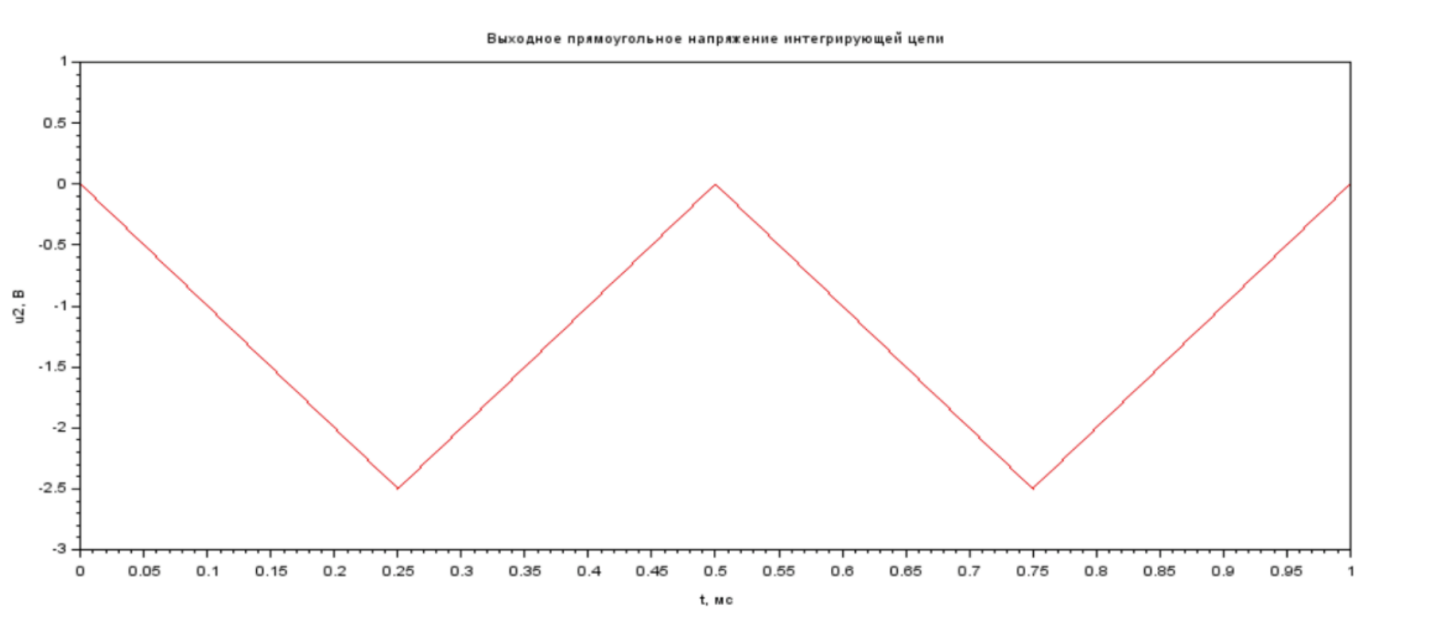
Рис. 1.4 График выходного прямоугольного напряжения интегрирующей цепи

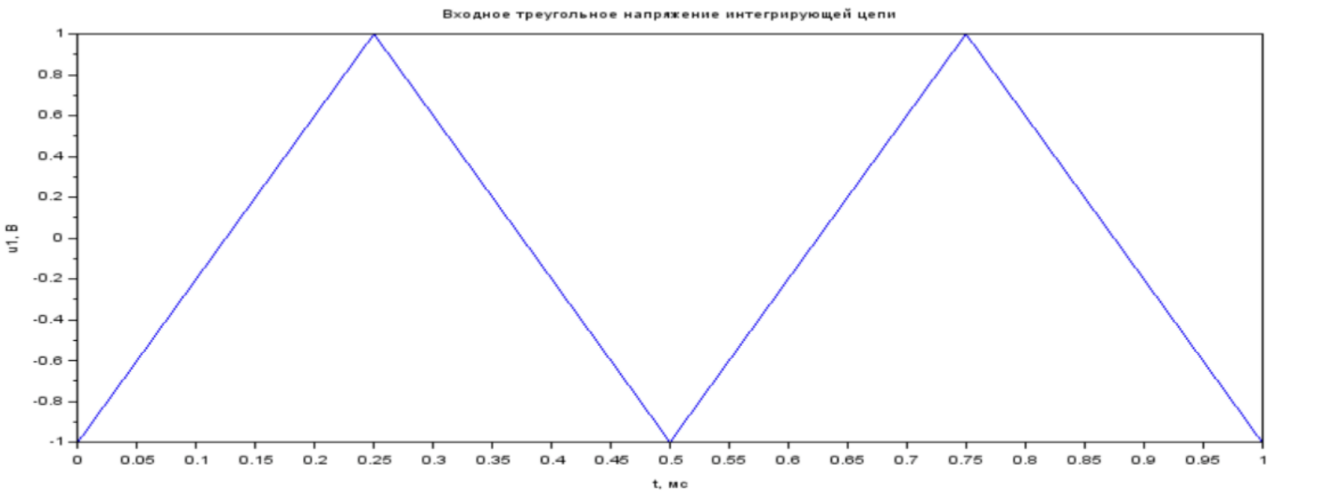
Рис. 1.5 График входного треугольного напряжения интегрирующей цепи

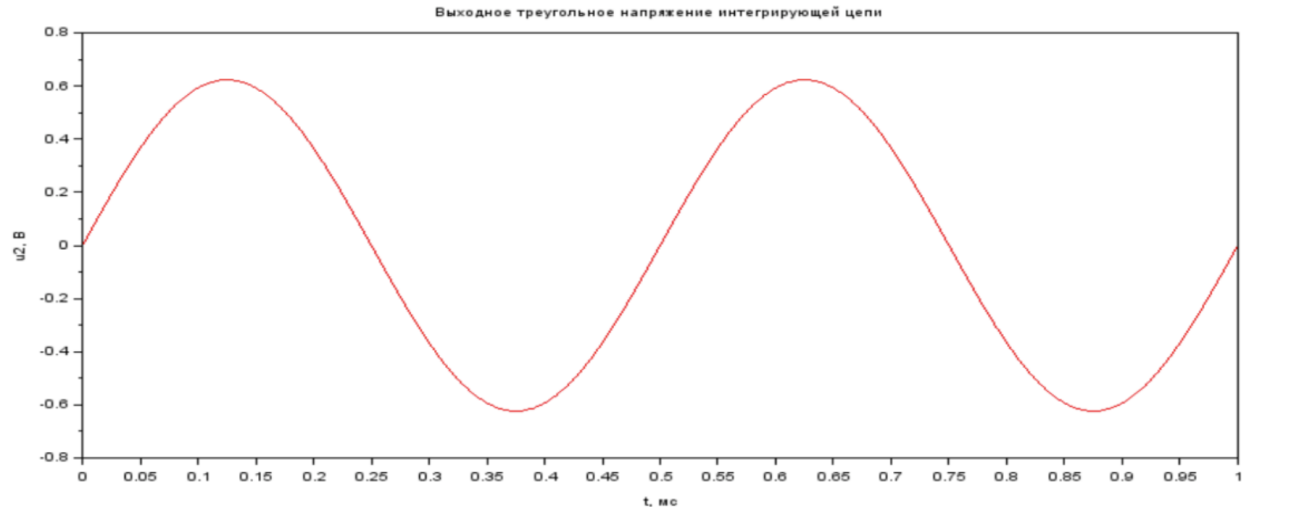
Рис. 1.6 График выходного треугольного напряжения интегрирующей цепи

Рис. 1.7 Расчет комплексной передаточной функции интегрирующей цепи при заданных параметрах

2. Для дифференцирующей цепи

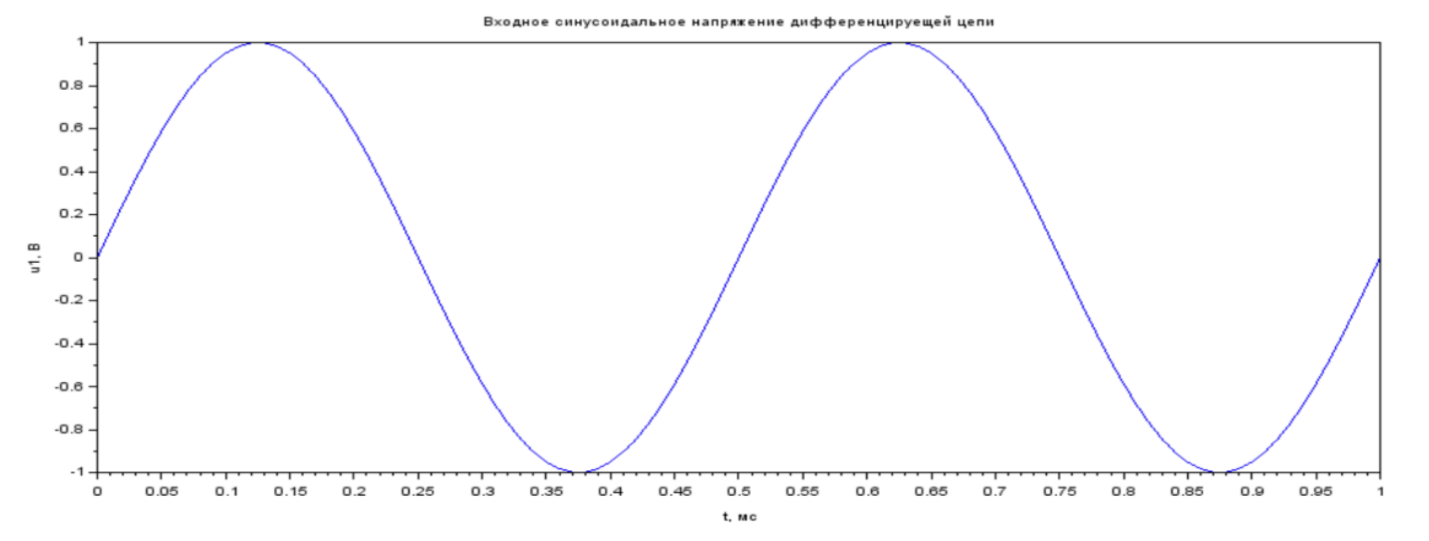
Рис. 2.1 График входного синусоидального напряжения дифференцирующей цепи

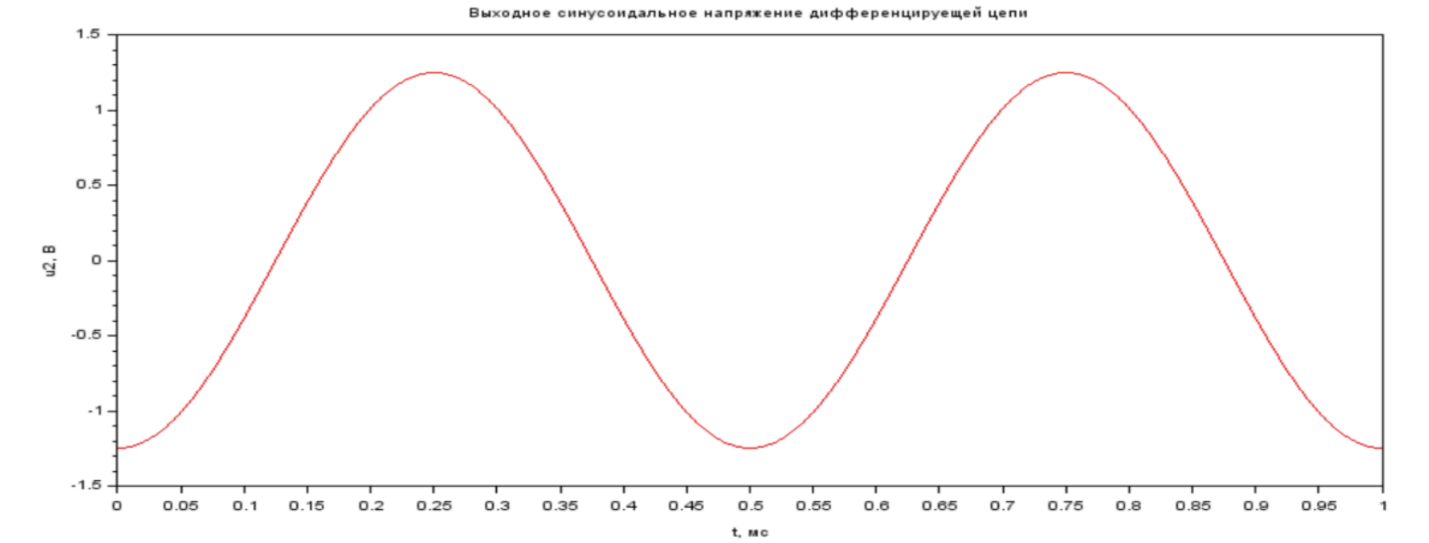
Рис. 2.2 График выходного синусоидального напряжения дифференцирующей цепи

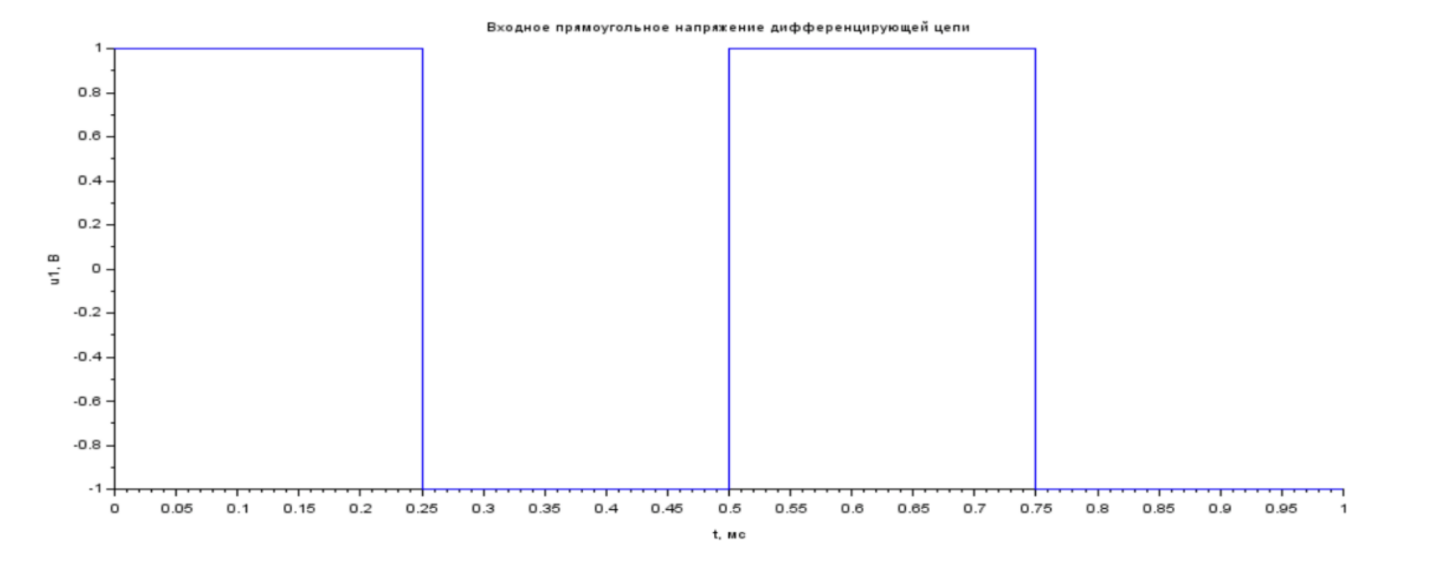
Рис. 2.3 График входного прямоугольного напряжения дифференцирующей цепи

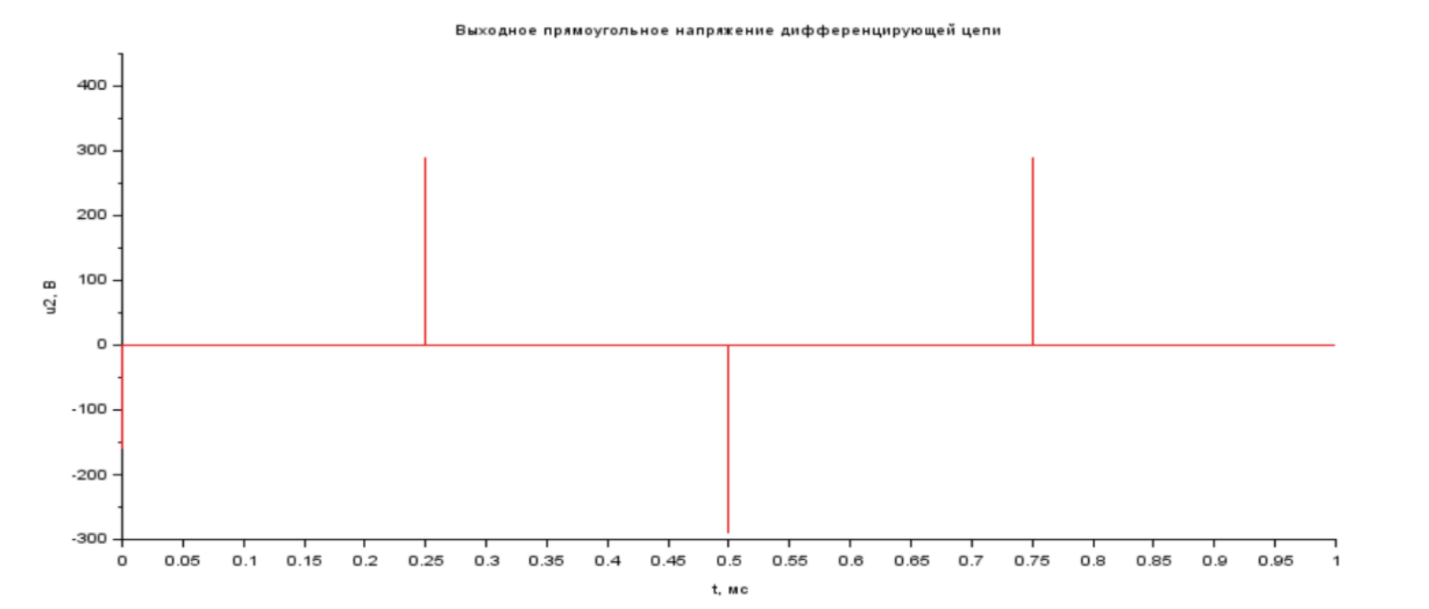
Рис. 2.4 График выходного прямоугольного напряжения дифференцирующей цепи

Рис. 2.5 График входного треугольного напряжения дифференцирующей цепи

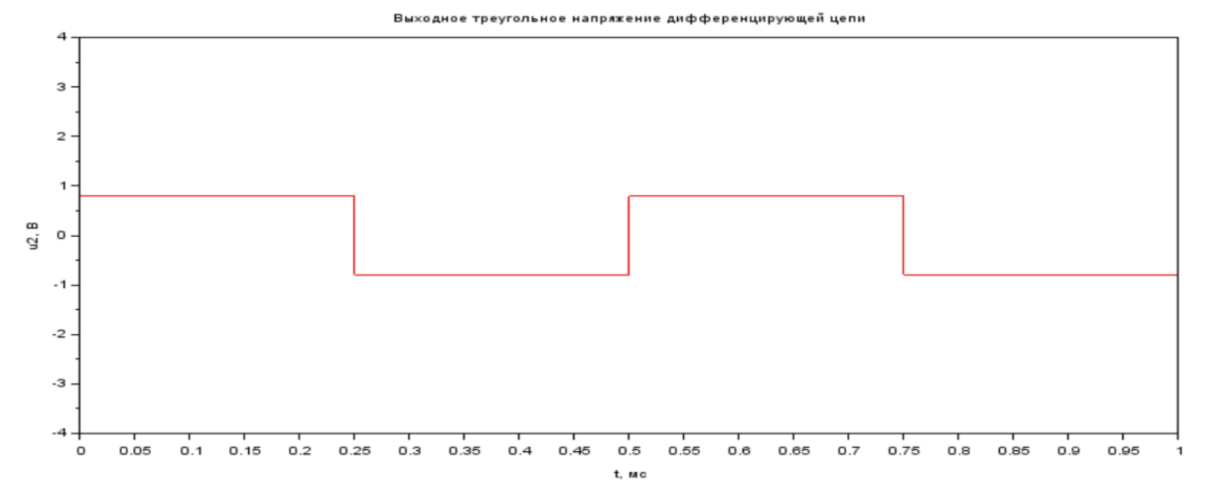
Рис. 2.6 График выходного треугольного напряжения дифференцирующей цепи

Рис. 2.7 Расчет комплексной передаточной функции дифференцирующей цепи при заданных параметрах

Экспериментальное исследование

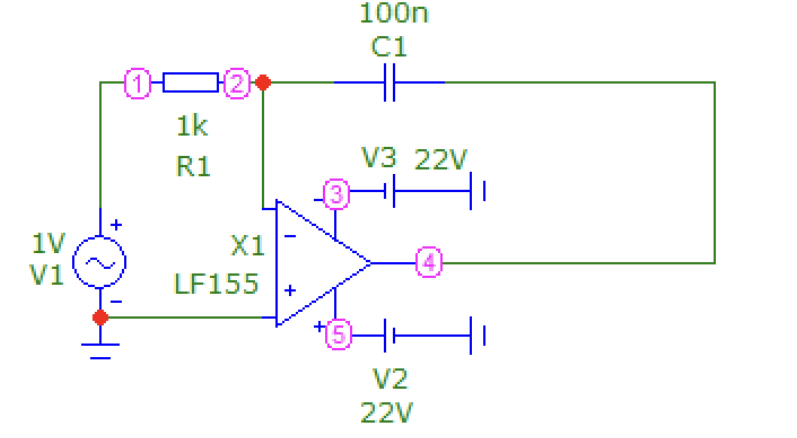
Рис. 3 Схема активной интегрирующей цепи

1. Для активной интегрирующей цепи с синусоидальным источником

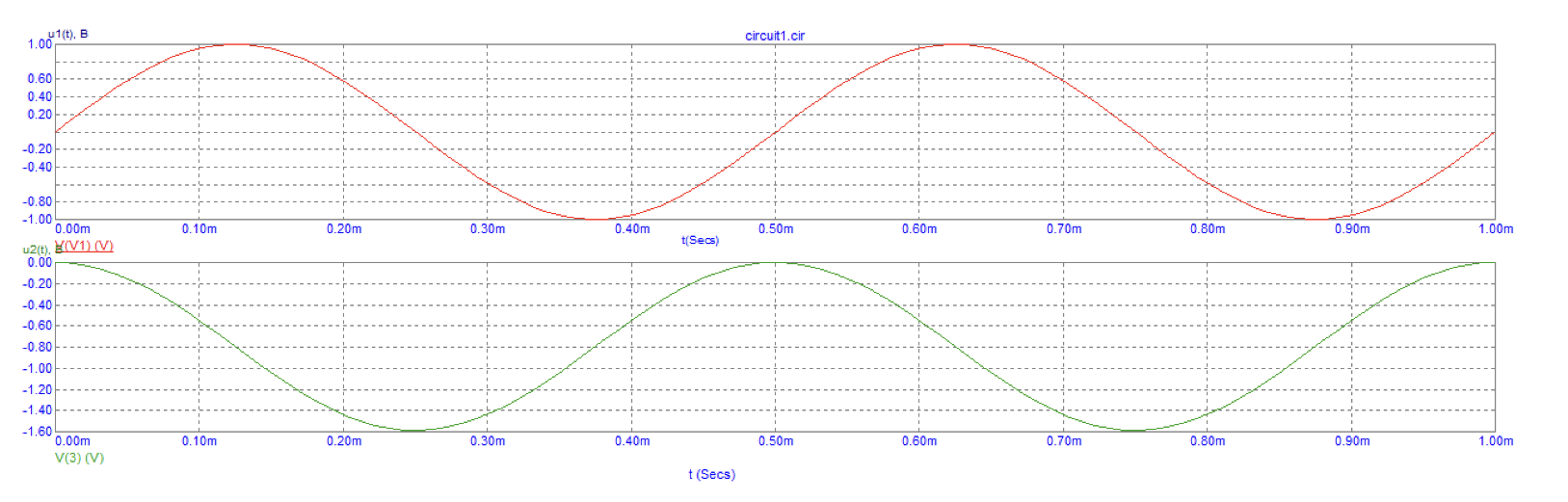
Рис. 4 Графики синусоидального напряжения на входе и на выходе интегрирующей цепи

Вывод: выходной сигнал интегрирующей активной цепи представляет собой проинтегрированный входной сигнал, то есть, синусоида заменилась косинусоидой.

2. Для активной интегрирующей цепи с импульсным источником:

Рис. 5 Схема активной интегрирующей цепи с импульсным источником напряжения

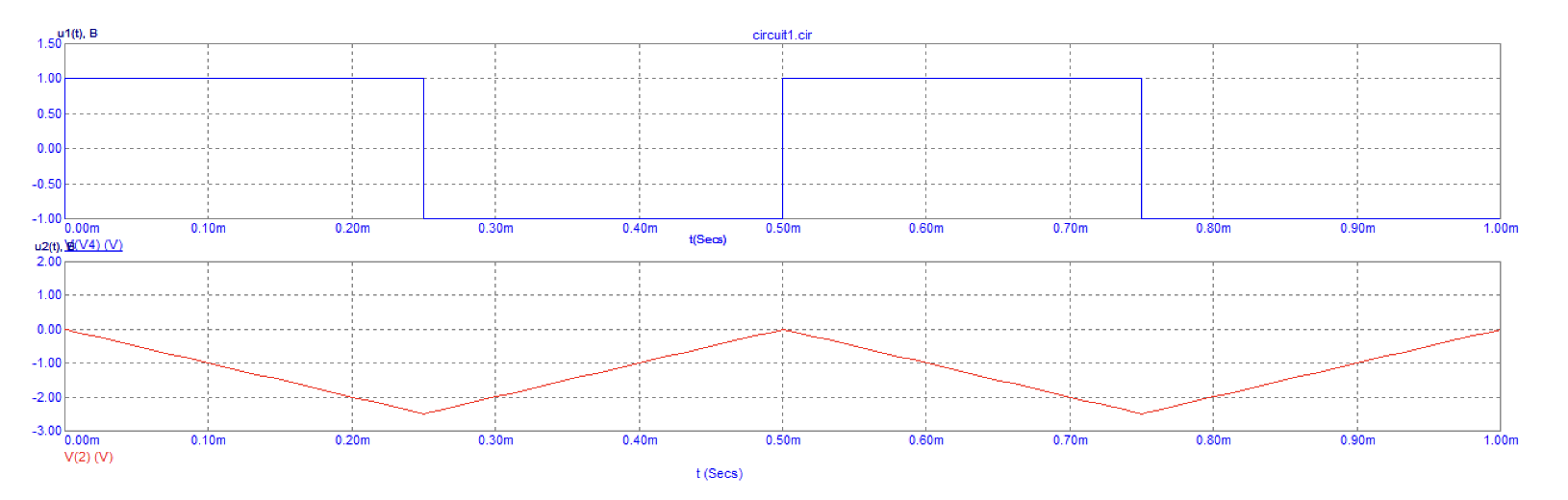
Рис. 6 Графики зависимости импульсного источника и выходного напряжения

Вывод: выходной сигнал интегрирующей активной цепи при прямоугольном воздействии представляет собой сигнал пилообразной формы, то есть, проинтегрированную прямоугольность последовательность импульсов.

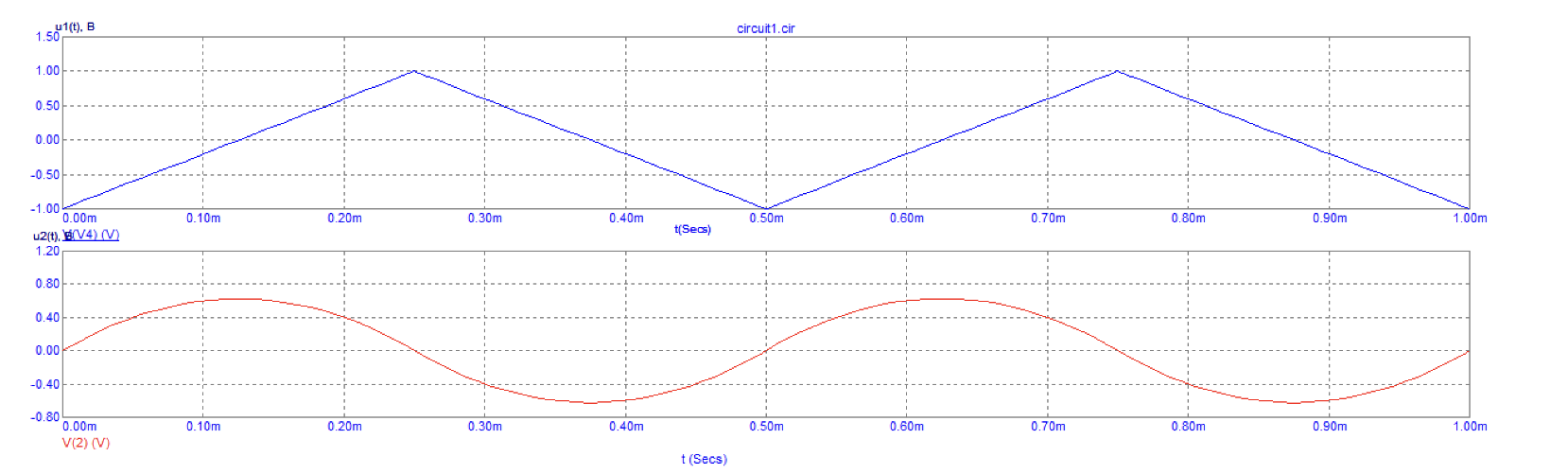
Рис. 7 Графики зависимости напряжения на выходе операционного усилителя и импульсного источника

Вывод: выходной сигнал интегрирующей активной цепи при треугольном воздействии представляет собой проинтегрированную пилообразную последовательность, то есть, синусоиду.

3. Для активной дифференцирующей цепи с синусоидальным источником

Рис. 8 Схема активной дифференцирующей цепи

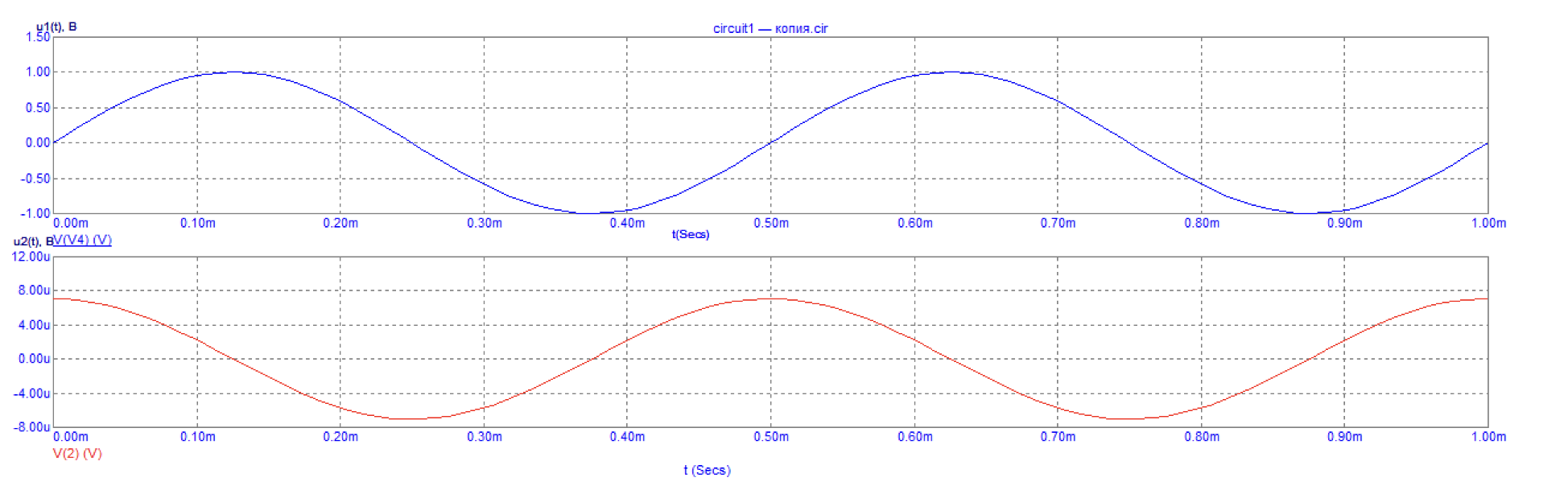
Рис. 9 Графики зависимости напряжений на входе и выходе дифференцирующей цепи от времени

Вывод: выходной сигнал дифференцирующей активной цепи при синусоидальном воздействии представляет собой продифференцированную синусоиду, то есть, косинусоиду.

4. Для активной дифференцирующей цепи с импульсным источником:

Рис. 10 Схема активной дифференцирующей цепи с импульсным источником напряжения

Рис. 11 Графики зависимости напряжений на входе и выходе дифференцирующей цепи от времени

Вывод: выходной сигнал дифференцирующей активной цепи при прямоугольном воздействии представляет собой повторяющуюся последовательность продифференцированных прямоугольных импульсов.

Рис. 12 Графики зависимости напряжений на входе и выходе дифференцирующей цепи от времени

Вывод: выходной сигнал дифференцирующей активной цепи при треугольном воздействии представляет собой повторяющуюся последовательность прямоугольных импульсов с небольшими искажениями, которые являются производной от пилообразной последовательности на входе.

Общий вывод: данные и графики, полученные в результате машинного эксперимента в программе Micro-Cap, полностью совпадают с данными и графиками, полученными в результате предварительного расчёта.

Практические задания и задачи к промежуточному контролю

1) Какие цепи являются интегрирующими? Приведите пример.

Интегрирующие цепи – такие цепи, у которых выходное напряжение пропорционально интегралу входного напряжения.

 

Пример: Нелинейный интегратор, фильтр нижних частот, линии задержки сигналов.

2) Какие цепи являются дифференцирующими? Приведите пример.

Дифференцирующие цепи – такие цепи, у которых выходной сигнал прямо пропорционален производной входного сигнала.

 

Пример: Фильтр верхних частот.

3) В каких случаях применяются интегрирующие цепи?

Интегрирующие цепи применяют для выполнения операций интегрирования в аналоговых вычислительных устройствах.

4) В каких случаях применяются дифференцирующие цепи?

Дифференцирующие цепи применяют тогда, когда требуется преобразовать входное напряжение в сигнал, изменяющийся по закону производной входного напряжения.

5) Нарисуйте схему интегратора на ОУ и выведите его передаточную функцию?

6) Нарисуйте схему дифференциатора на ОУ и выведите его передаточную функцию?

7) Нарисуйте схему пассивного интегратора.