Лабы / Лабораторная работа №31

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра теории электрических цепей

Лабораторная работа №31

по дисциплине

Теоретические основы электротехники

на тему

Исследование входных частотных характеристик в RL-цепи

Проверил: к.т.н Мосичев А. В.

Москва, 2023

Цель работы: С помощью программы Micro-Cap исследовать входные амплитудно-частотные (АЧХ) и фазочастотные (ФЧХ) характеристики RL-цепи. Сравнить АЧХ и ФЧХ, полученные с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчётным путём.

Исходные данные:

R₁ = 121 Ом, L₁ = 45 мГн;

f = 2, 4, 6, 8, 10, 12, 14 кГц, E = 0,9 B;

 , где  – комплексное входное напряжение;

 – комплексный входной ток;

U_R = R • I – комплексное напряжение на резисторе;

 – мнимая единица;

 – угловая частота;

f – частота;

 – комплексное напряжение на катушке;

 – модуль комплексного входного сопротивления (АЧХ);

 – аргумент (фаза) комплексного входного сопротивления (ФЧХ).

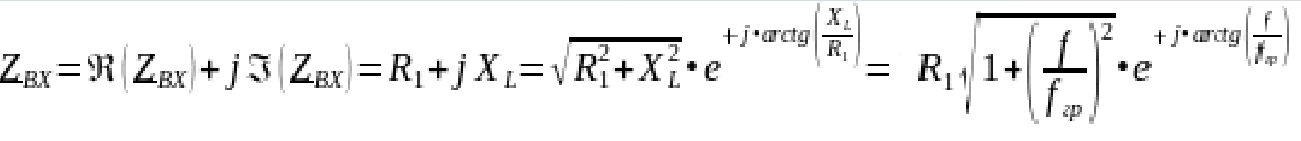, где Re(Z_BX) = R₁ – резистивное входное сопротивление (равно сопротивлению резистора R₁),

Im(Z_BX) = X_L – реактивное входное сопротивление,

 – индуктивное сопротивление катушки L₁.

f_гр =   – граничная частота RL-цепи.

Предварительный расчёт

1. Расчёт и построение графика зависимости модуля входного сопротивления от частоты.

Рис. 1.1 Расчёт зависимости модуля входного сопротивления от частоты

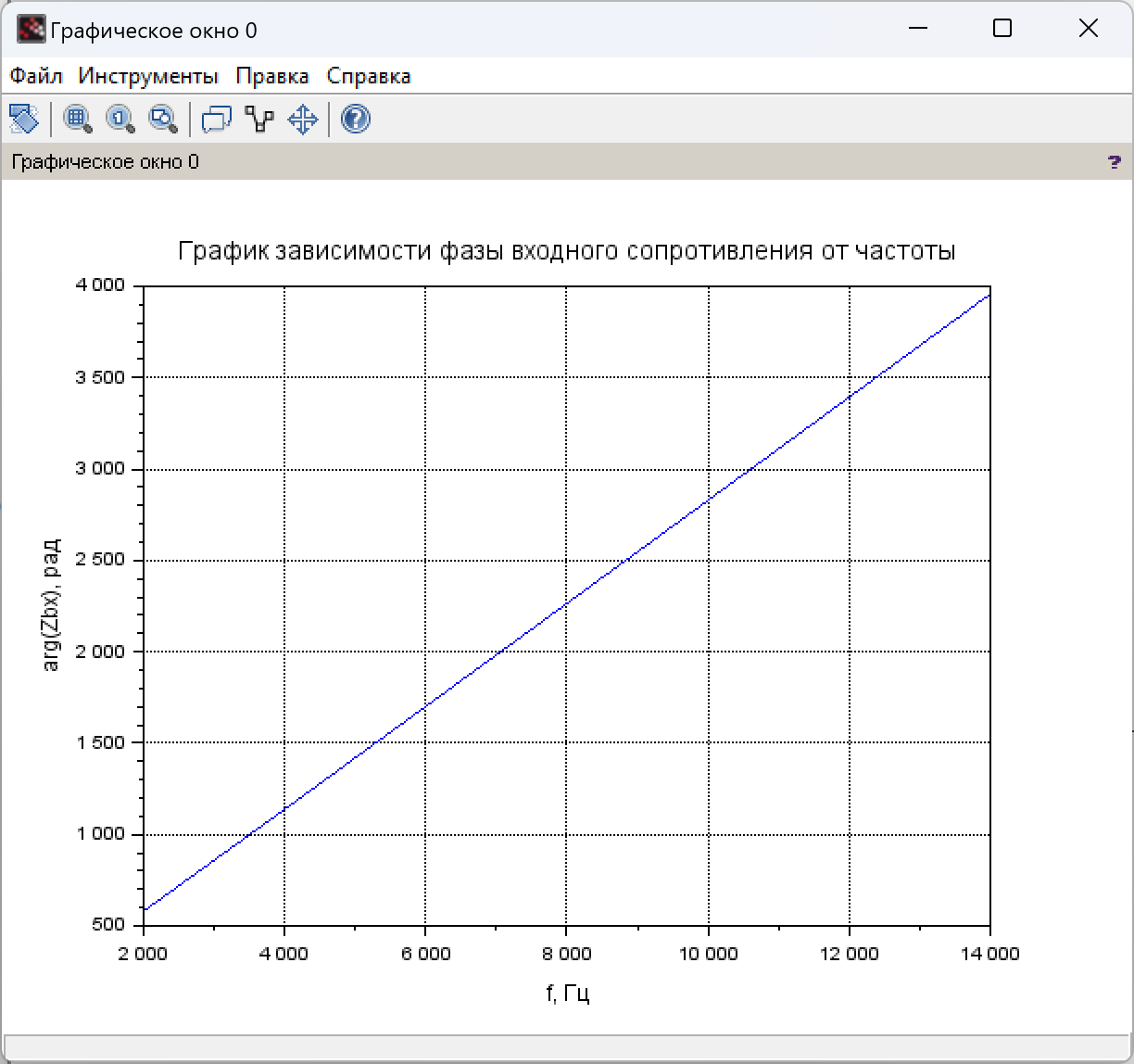
Рис. 1.2 График зависимости модуля входного сопротивления от частоты

2. Расчёт и построение графика зависимости фазы входного сопротивления от частоты.

Рис. 2.1 Расчёт зависимости фазы входного сопротивления от частоты

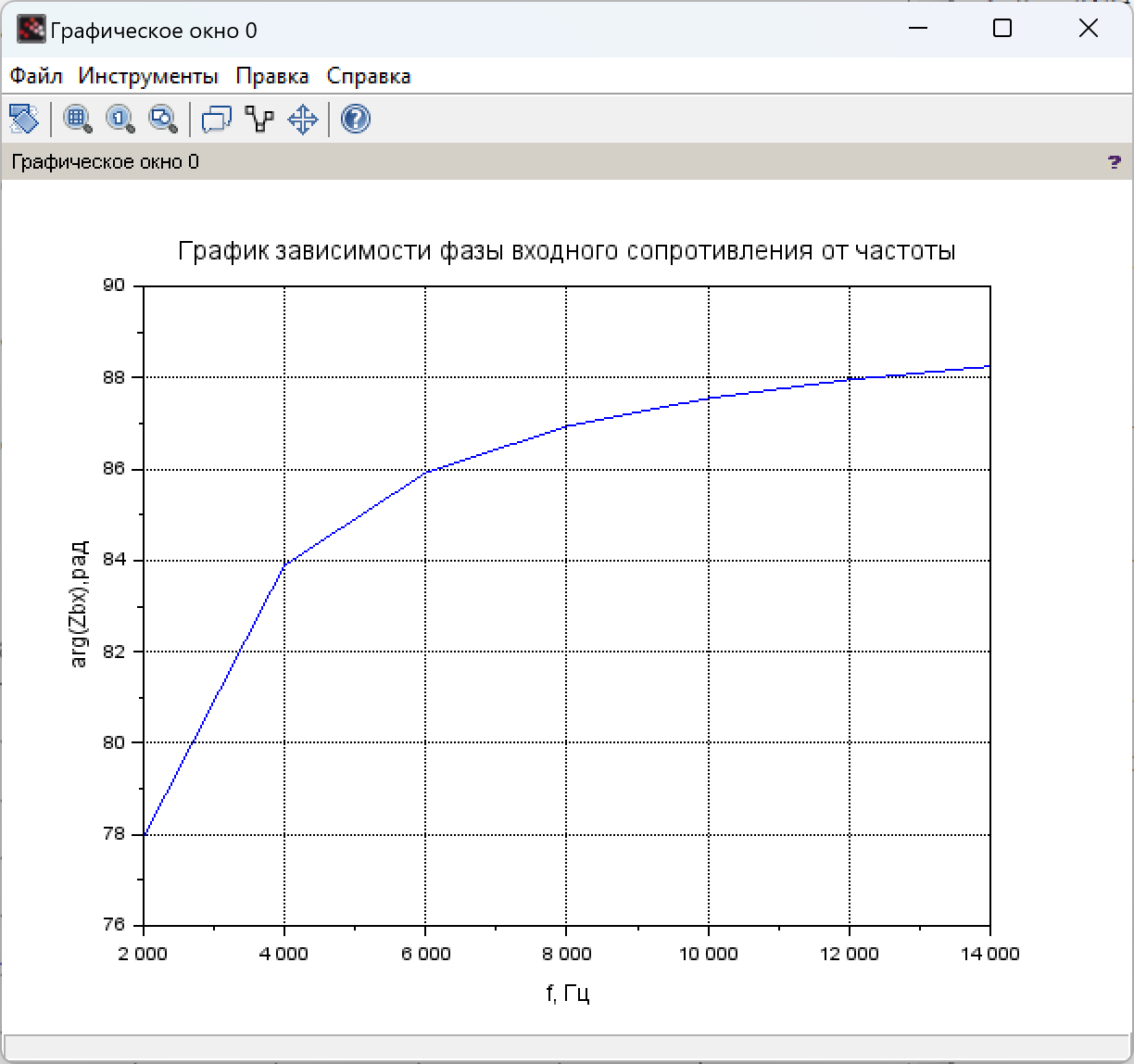
Рис. 2.2 График зависимости фазы входного сопротивления от частоты

3. Расчёт и построение зависимости модуля тока от частоты.

Рис. 3.1 Расчёт зависимости модуля тока от частоты

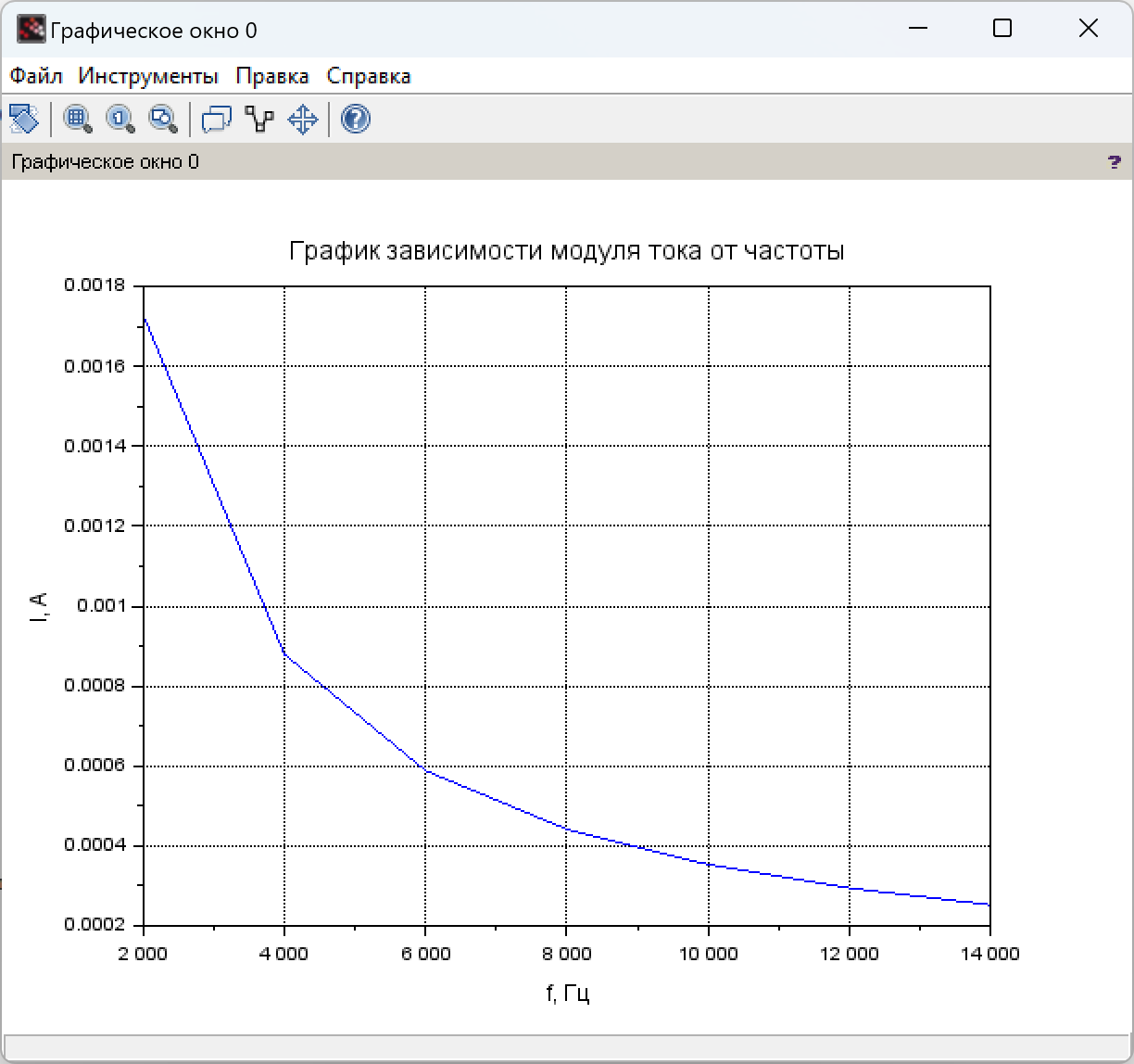
Рис. 3.2 График зависимости модуля тока от частоты

4. Расчёт и построение зависимости модуля напряжения на резисторе от частоты.

Рис. 4.1 Расчёт зависимости модуля напряжения на резисторе от частоты

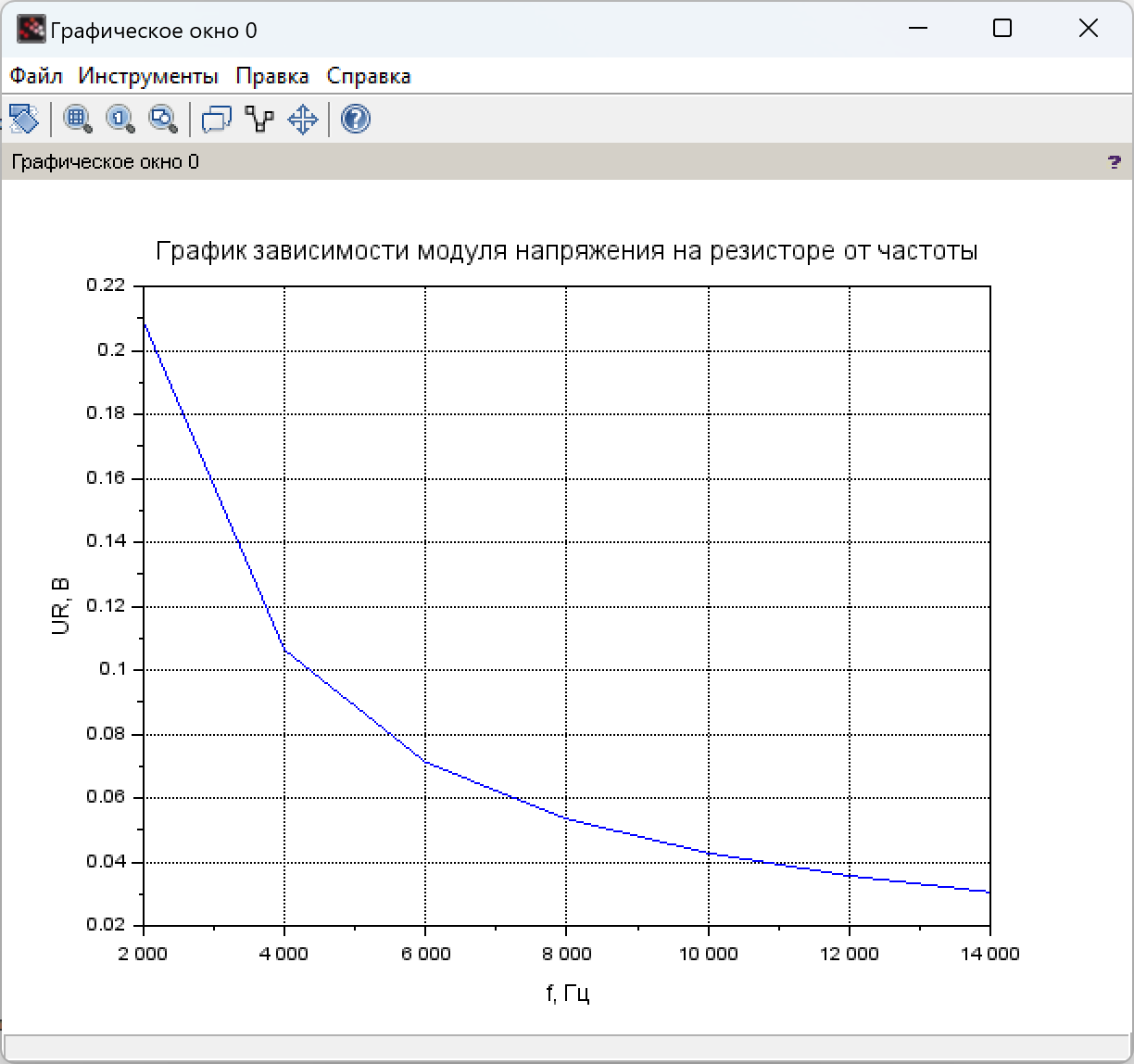
Рис. 4.2 График зависимости модуля напряжения на резисторе от частоты

5. Расчёт и построение зависимости резистивного сопротивления от частоты.

Рис. 5.1 Расчёт зависимости резистивного сопротивления от частоты

Рис. 5.2 График зависимости резистивного сопротивления от частоты

6. Расчёт и построение зависимости индуктивного сопротивления от частоты.

Рис. 6.1 Расчёт зависимости индуктивного сопротивления от частоты

Рис. 6.2 График зависимости индуктивного сопротивления от частоты

7. Расчёт и построение зависимости модуля напряжения на катушке от частоты.

Рис. 7.1 Расчёт зависимости модуля напряжения на катушке от частоты

Рис. 7.2 График зависимости модуля напряжения на катушке от частоты

8. Расчёт и построение зависимости частоты от граничной частоты.

Рис. 8.1 Расчёт зависимости частоты от граничной частоты

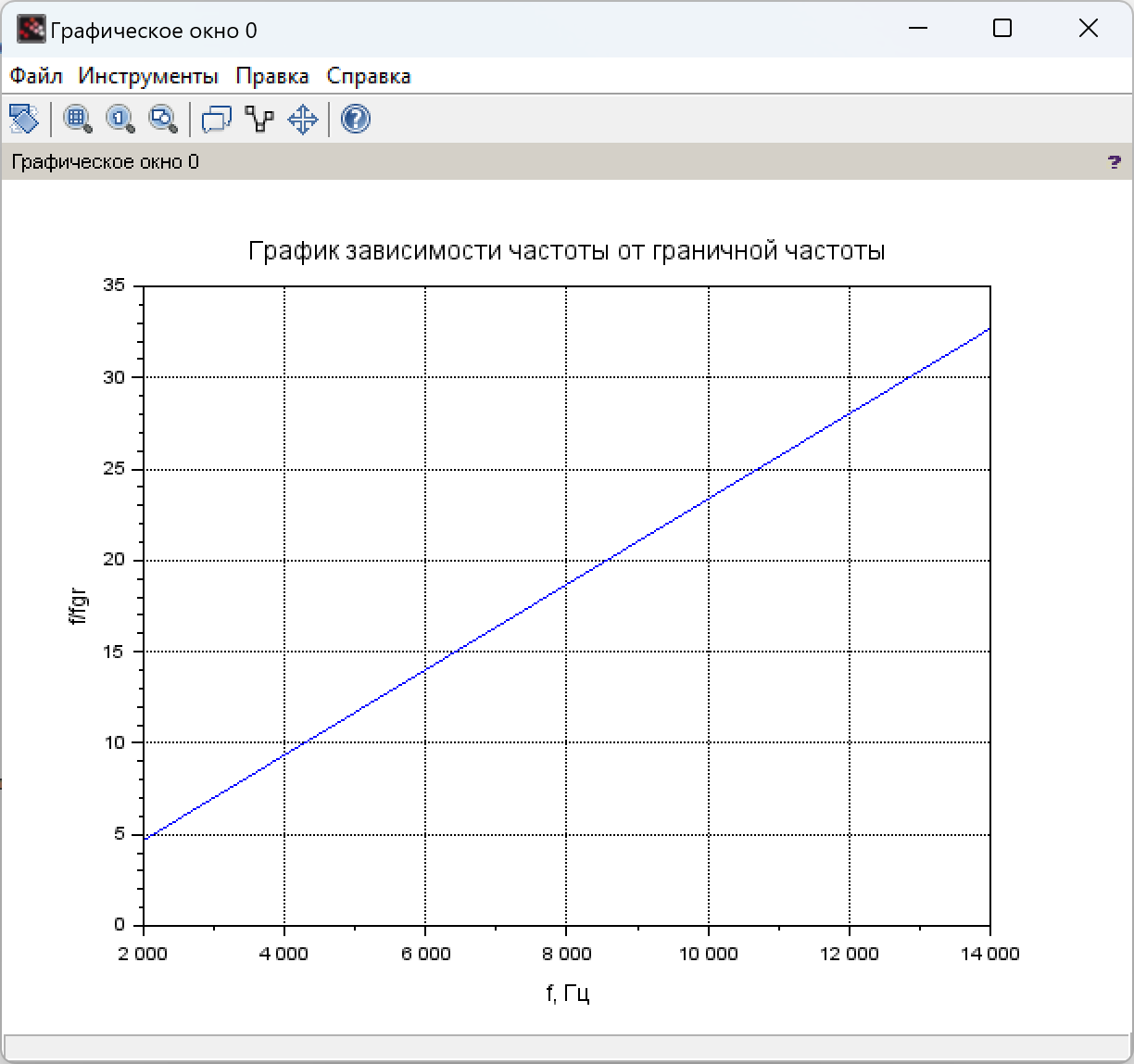
Рис. 8.2 График зависимости частоты от граничной частоты

Экспериментальное исследование

Рис. 9 Схема RL-цепи

1. Зависимость модуля входного сопротивления от частоты.

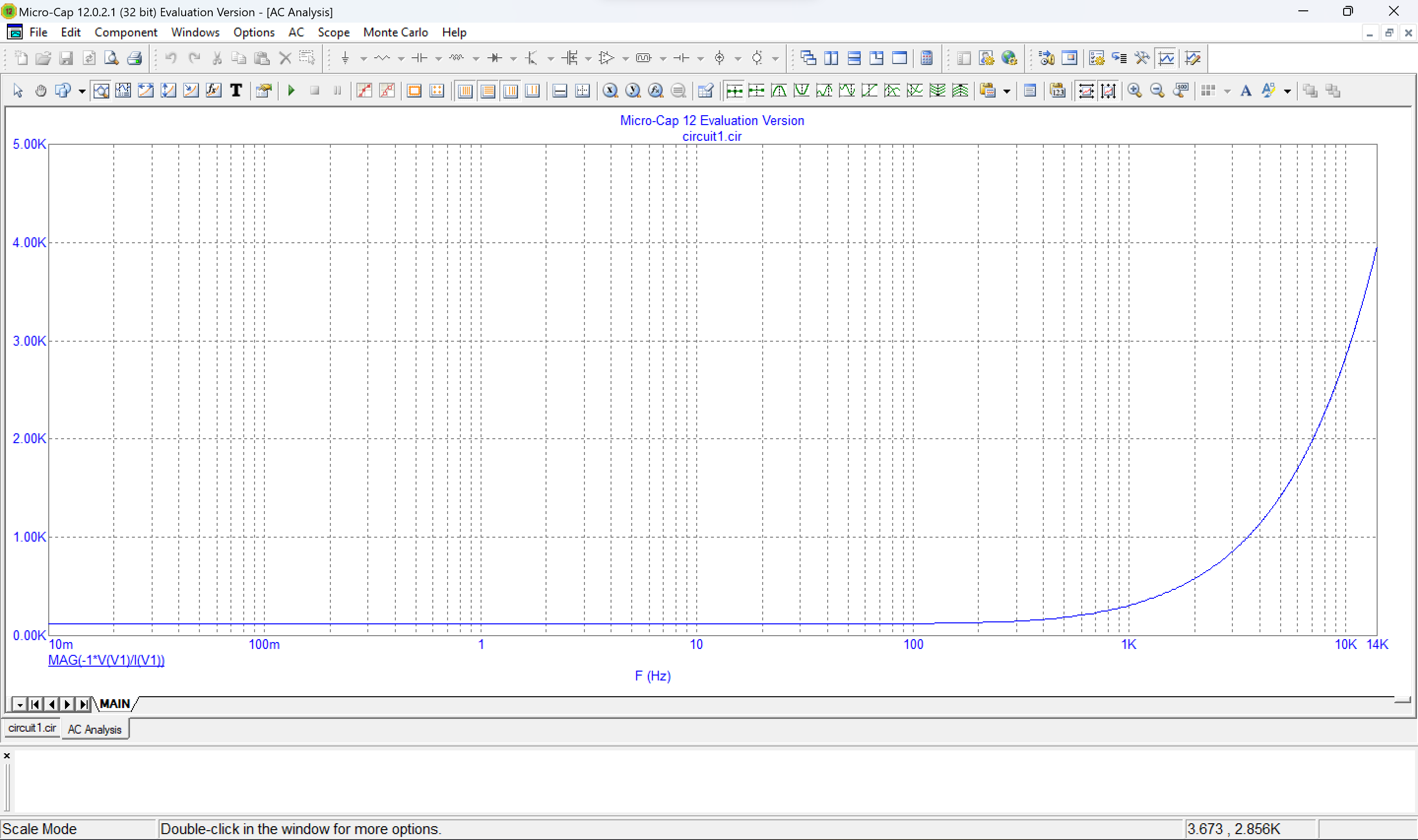
Рис. 10 График зависимости модуля входного сопротивления от частоты

Вывод: при увеличении частоты увеличивается модуль входного сопротивления.

2. Зависимость фазы входного сопротивления от частоты.

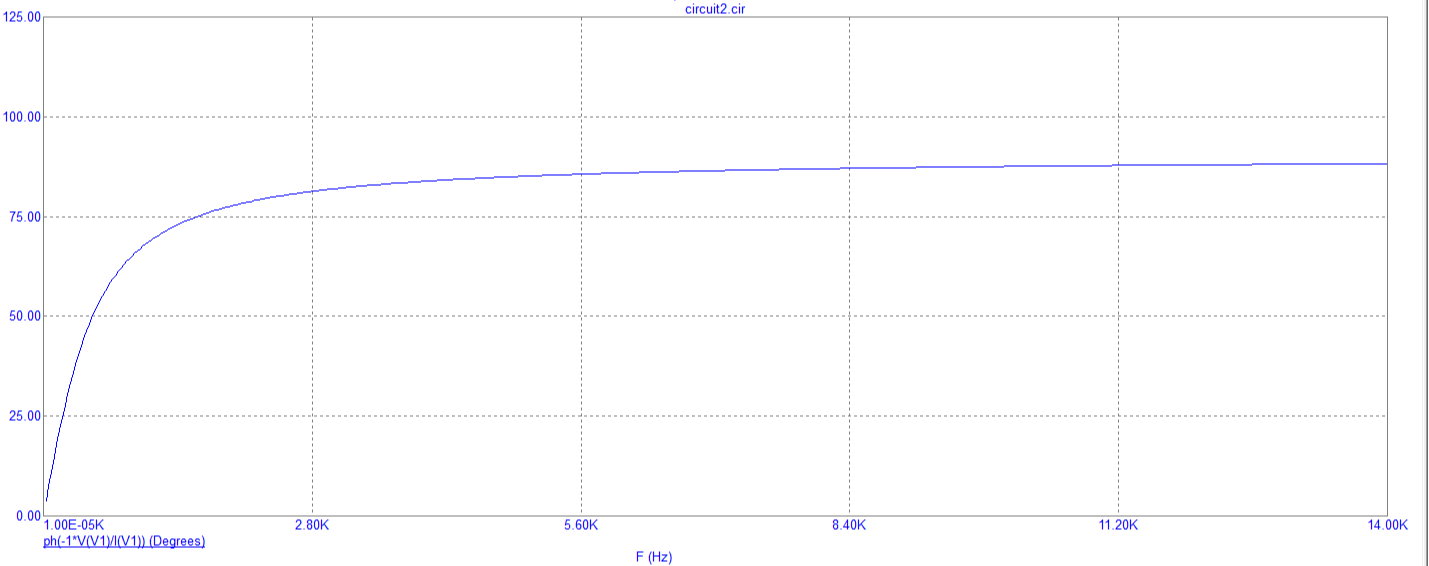
Рис. 11 График зависимости фазы входного сопротивления от частоты

Вывод: при увеличении частоты увеличивается фаза входного сопротивления.

3. Зависимость модуля тока от частоты.

Рис. 12 График зависимости модуля тока от частоты

Вывод: при увеличении частоты уменьшается модуль тока.

4. Зависимость модуля напряжения на резисторе от частоты.

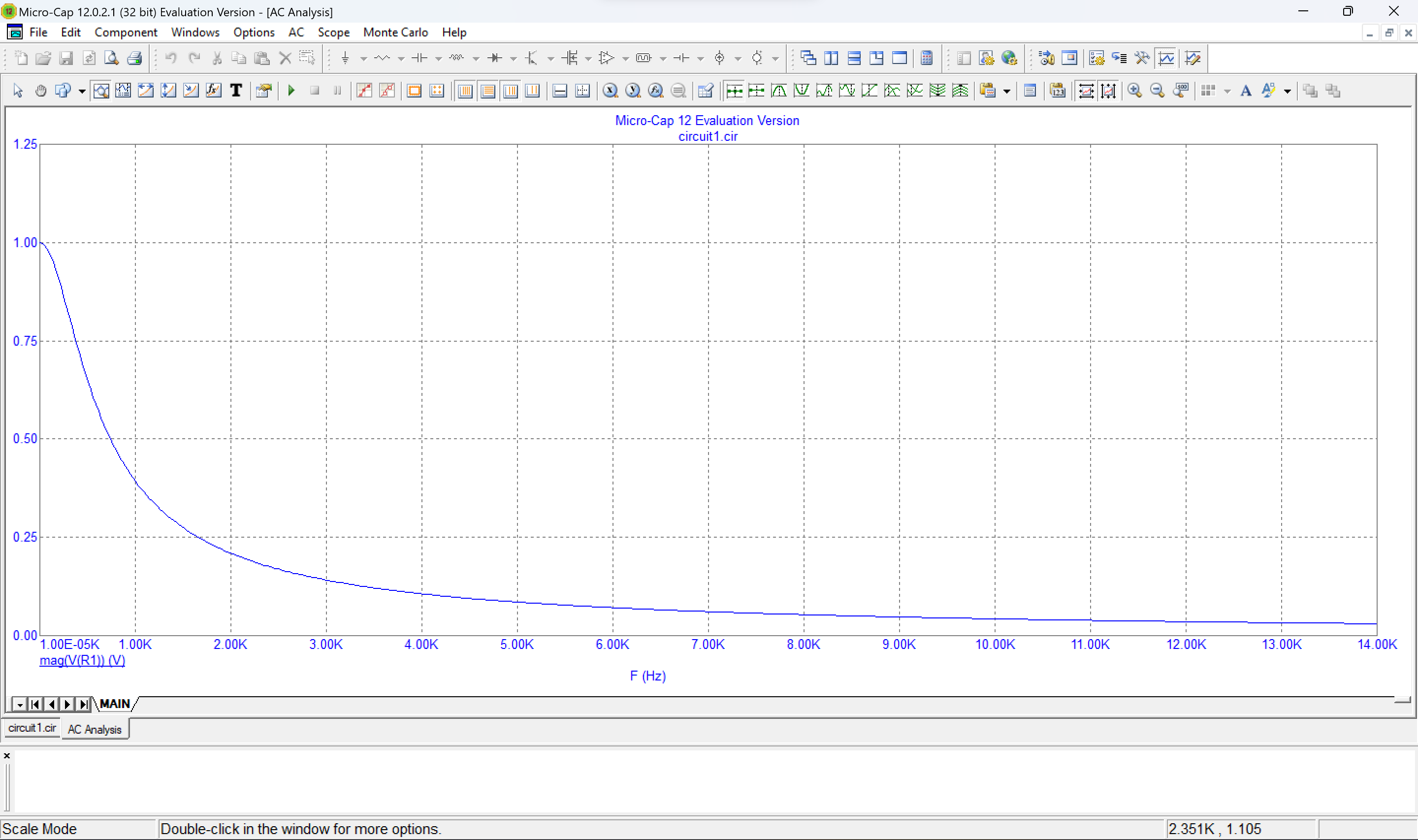
Рис. 13 График зависимости модуля напряжения на резисторе от частоты

Вывод: при увеличении частоты уменьшается модуль напряжения на резисторе.

5. Зависимость резистивного сопротивления от частоты

Рис. 14 График зависимости резистивного сопротивления от частоты

Вывод: при увеличении частоты резистивное сопротивление остается неизменным.

6. Зависимость индуктивного сопротивления от частоты

Рис. 15 График зависимости индуктивного сопротивления от частоты

Вывод: при увеличении частоты увеличивается индуктивное сопротивление.

7. Зависимость модуля напряжения на катушке от частоты

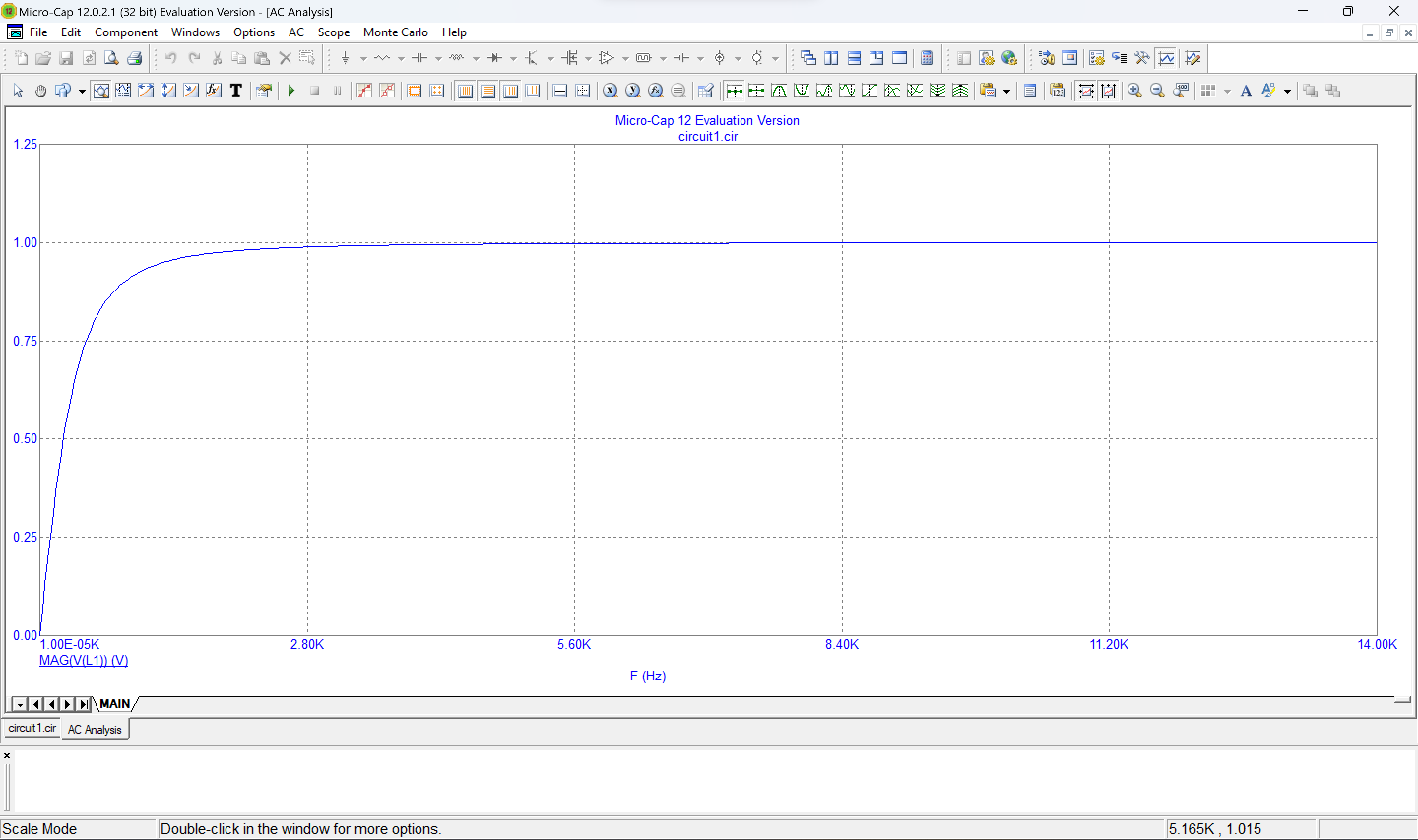
Рис. 16 График зависимости модуля напряжения на катушке от частоты

Вывод: при увеличении частоты увеличивается модуль напряжения на катушке.

8. Зависимость частоты от граничной частоты

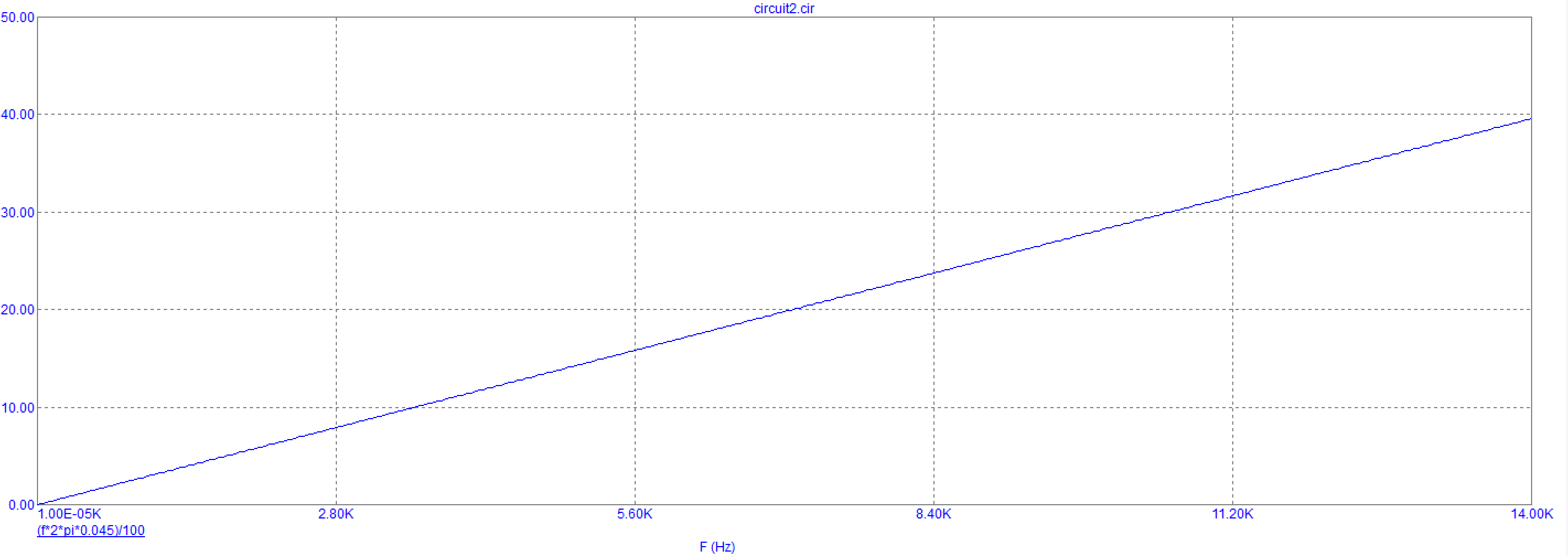
Рис. 17 График зависимости частоты от граничной частоты

Вывод: при увеличении частоты увеличивается граничная частота.

Таблица расчётов

Таблица 1 – Таблица расчётов

Получено экспериментально
f, кГц	f/fгр	XL, Ом	Zbx, Ом	Ф, град.	I, mA	Ur, В	UL, В
2	5,65	565	578,3	77,9	1,72	0,22	0,975
4	11,3	1130	1137,3	83,9	0,87	0,11	0,993
6	16,9	1696	1701,4	85,9	0,58	0,071	0,997
8	22,6	2261	2265,9	86,9	0,44	0,056	0,998
10	28,2	2827	2830,4	87,5	0,35	0,045	0,998
12	33,9	3393	3395,9	87,9	0,29	0,038	0,999
14	39,5	3956	3960	88,2	0,25	0,032	0,999

Продолжение таблицы 1

По предварительному расчёту
f, кГц	f/fгр	XL, Ом	Zbx, Ом	Ф, град.	I, mA	Ur, В	UL, В
2	4,67	565	574,2	77,92	1,73	0,21	0,977
4	9,34	1130	1135	83,89	0,88	0,11	0,994
6	14,02	1696	1699	85,92	0,588	0,071	0,997
8	18,69	2262	2264	86,93	0,441	0,053	0,998
10	23,36	2827	2829	87,54	0,353	0,043	0,999
12	28,04	3393	3394	87,96	0,294	0,036	0,999
14	32,71	3958	3960	88,25	0,252	0,031	0,999

Общий вывод: данные и графики, полученные в результате машинного эксперимента в программе Micro-Cap, практически полностью совпадают с данными и графиками, полученными в результате предварительного расчёта.

Вопросы для самопроверки

1. Какая частота называется граничной для RL-цепи?

2. Каково значение модуля входного сопротивления RL-цепи на граничной частоте?

3. Каково значение аргумента входного сопротивления RL-цепи на граничной частоте?

4. К чему стремится модуль тока RL-цепи при увеличении частоты?

5. Чему равен модуль входного сопротивления RL-цепи при частоте, равной нулю?

Ответы:

1. Граничная частота RL-цепи – частота, на которой действительная и мнимая часть комплексного входного сопротивления равны.

2. На граничной частоте:   ,   ,   , т.е.   = 2  . Подставив числовые значения, получим: |Zвх| = R  = 4241,28 Ом. Ответ: 4241,28 Ом

3. На граничной частоте:  arg|Zвх|= =|φвх|, соответственно, arg|Zвх|= 44,98°

Ответ: 44,98°

4.  ;   ; . С ростом частоты входное напряжение цепи возрастает, а модуль тока уменьшается, следовательно, 

Ответ: U

5.   ;    Соответственно, 

Ответ: 3000 Ом