Лабы / Лабораторная работа №30

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра теории электрических цепей

Лабораторная работа №30

по дисциплине

Теоретические основы электротехники

на тему

Моделирование на ЭВМ переходных процессов в цепях первого порядка

Проверил: к.т.н Мосичев А. В.

Москва, 2023

Цель работы: c помощью машинного эксперимента исследовать переходные процессы в цепях первого порядка.

Исходные данные:

Для неразветвленной RC-цепи:

C₁ = 0,25 мкФ; R₁ = 20, 40, 80, 160, 320, 640, 1280, 2560, 5120 Ом;

Для неразветвленной RL-цепи:

L₁ = 45 мГн; R₁ = 20, 40, 80, 160, 320, 640, 1280, 2560, 5120 Ом;

Для неразветвленной RC-цепи на постоянном напряжении:

E₁ = 1 В; R₁ = 160 Ом; C₁ = 0,25 мкФ; t   [0; 3τ_RC];

Для неразветвленной RL-цепи на постоянном напряжении:

E₁ = 1 В; R₁ = 160 Ом; L₁ = 45 мГн; t [0; 3τ_RL];

τ_RC = R * C;

 (t) = 

 (t) = 

 (t) = 

τ_RL =   ;

i(t) =   .

Предварительный расчёт

1. Расчет постоянной времени для неразветвленной RC-цепи

Рис. 1 Расчет постоянной времени для неразветвленной RC-цепи

2. Расчет постоянной времени для неразветвленной RL-цепи

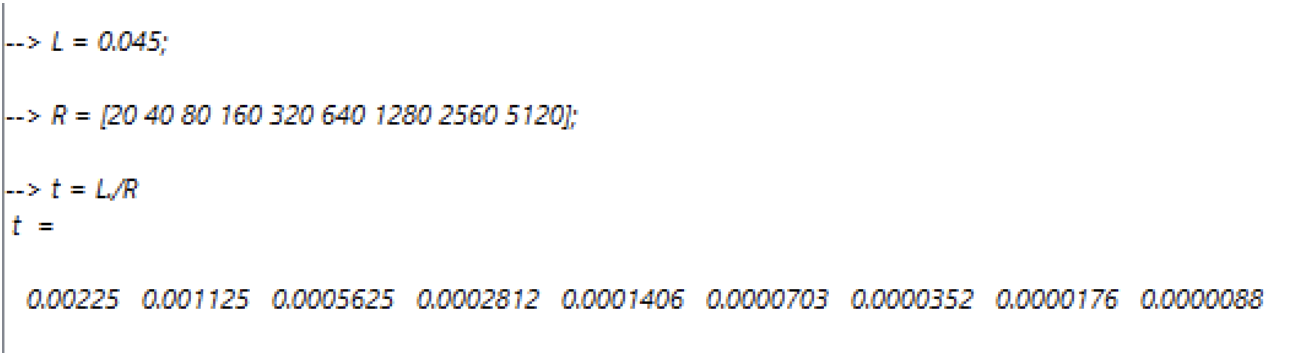
Рис. 2 Расчет постоянной времени для неразветвленной RL-цепи

3. Построение и расчёт временных зависимостей тока, напряжения на резисторе и напряжения на конденсаторе в неразветвленной RC-цепи при постоянном напряжении

Рис. 3.1 Расчёт зависимости напряжения на конденсаторе и резисторе от времени

Рис. 3.2 Графики временных зависимостей напряжения на резисторе и напряжения на конденсаторе в неразветвленной RC-цепи при постоянном напряжении

Рис. 3.3 График временной зависимости тока в неразветвленной RC-цепи при постоянном напряжении

Рис. 3.4 Расчет величин

4. Построение и расчет временных зависимостей тока, напряжения на резисторе и напряжения на катушке в неразветвленной RL-цепи при постоянном напряжении

Рис. 4.1 Расчёт зависимости напряжения на катушке и резисторе от времени

Рис. 4.2 Графики временных зависимостей напряжения на резисторе и напряжения на катушке в неразветвленной RL-цепи при постоянном напряжении

Рис. 4.3 График временной зависимости тока в неразветвленной RL-цепи при постоянном напряжении

Рис. 4.4 Расчет величин

Экспериментальное исследование

Рис. 5 Схема RC-цепи

1. Зависимости мгновенного тока, напряжения на резисторе, напряжения на конденсаторе и напряжения источника от времени для RC-цепи

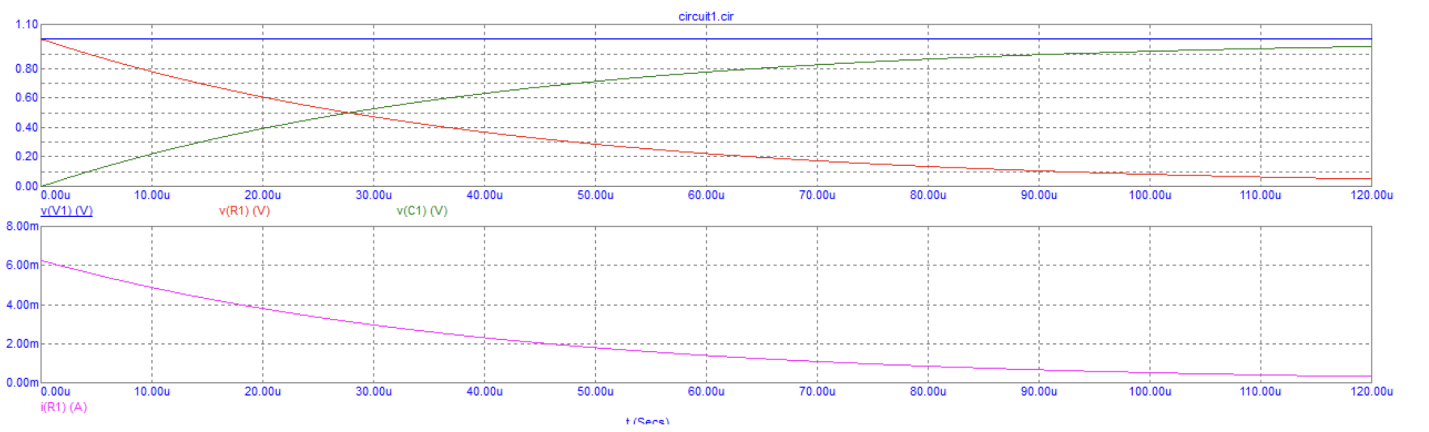
Рис. 6 Графики зависимости мгновенного тока, напряжения на резисторе, напряжения на конденсаторе и напряжения источника от времени для RC-цепи

Вывод: при увеличении времени: уменьшается мгновенный ток, уменьшается напряжение на резисторе, увеличивается напряжение на конденсаторе и остается неизменным напряжение источника.

Рис. 7 Схема RL-цепи

2. Зависимости мгновенного тока, напряжения на резисторе, напряжения на катушке и напряжения источника от времени для RL-цепи

Рис. 8 Графики зависимости мгновенного тока, напряжения на резисторе, напряжения на катушке и напряжения источника от времени для RL-цепи

Вывод: при увеличении времени: увеличивается мгновенный ток, увеличивается напряжение на резисторе, уменьшается напряжение на катушке и остается неизменным напряжение источника.

Таблица 1 – Результаты эксперимента

По предварительному расчету (C1 = 0,25 мкФ, L1 = 45 мГн)
R1, Ом	20	40	80	160	320	640	1280	2560	5120
RC, мкс	0,5 * 10-5	1 * 10-5	2 * 10-5	4 * 10-5	8 * 10-5	16 * 10-5	32 * 10-5	64 * 10-5	128 * 10-5
RL, мкс	225 * 10-5	1125 * 10-6	5625 * 10-7	2812 * 10-7	1406 * 10-7	703 * 10-7	352 * 10-7	176 * 10-7	88 * 10-7
По экспериментальным данным
RC, мкс	0,5 * 10-5	1 * 10-5	2 * 10-5	4 * 10-5	8 * 10-5	16 * 10-5	32 * 10-5	64 * 10-5	128 * 10-5
RL, мкс	225 * 10-5	1125 * 10-6	5625 * 10-7	2812 * 10-7	1406 * 10-7	703 * 10-7	352 * 10-7	176 * 10-7	88 * 10-7

Общий вывод: данные и графики, полученные в результате машинного эксперимента в программе Micro-Cap, полностью совпадают с данными и графиками, полученными в результате предварительного расчёта.

Практические задания и задачи к промежуточному контролю

1. Что называется переходным процессом? Приведите пример.

Ответ: Переходным процессом называется процесс перехода цепи от одного установившегося режима к другому. Пример: цепи, ещё не подключившиеся к источнику электрического сигнала, т.е. цепи, в которых ещё нет токов.

2. Какие цепи называют цепями первого порядка?

Ответ: Порядок электрической цепи определяется числом реактивных элементов. Цепь первого порядка (n = 1) включает один реактивный элемент – индуктивность или ёмкость и любое число резистивных элементов и независимых источников питания.

3. Какой режим называется установившемся?

Ответ: Режим называется установившимся, если параметры цепи либо постоянны во времени, либо постоянны по амплитуде токи и напряжения.

4. Какой физический смысл постоянной временной цепи?

Ответ: Физически постоянная времени цепи определяет время, в течение которого свободная составляющая тока или свободная составляющая напряжения в цепи уменьшается в e раз.

5. Как по графику рассчитать постоянную времени цепи?

Ответ: Чтобы по графику рассчитать постоянную времени цепи, необходимо воспользоваться следующем формулой:

6. Как можно определить стабильность переходного процесса в цепи первого порядка?

Ответ: Переходный процесс в цепи первого порядка является устойчивым, если амплитуда сигнала не бесконечно возрастает или не бесконечно убывает со временем.

7. Какой вид имеет переходная функция цепи первого порядка?

Ответ: Переходная функция цепи первого порядка имеет вид экспоненциальной функции.