Лабы / Лабораторная работа №16

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра теории электрических цепей

Лабораторная работа №16

по дисциплине

Теоретические основы электротехники

на тему

Исследование на ЭВМ резонансных явлений в пассивном и активном последовательном колебательном контуре

Проверил: к.т.н Мосичев А. В.

Москва, 2023

Цель работы: с помощью программы Micro-Cap исследовать характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.

Исходные данные:

 – комплексное входное сопротивление контура;

 – резонансная частота контура;

 – частота;

 – характеристическое сопротивление;

 – добротность;

 – нижняя граничная частота;

 – верхняя граничная частота;

П = f₂ – f₁ – абсолютная полоса пропускания;

 – модуль входного тока при резонансе;

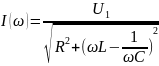 – резонансная кривая тока при условии, что меняется только частота источника напряжения.

Предварительный расчёт

1. Расчет для пассивного последовательного колебательного контура.

Рис. 1.1 Расчет величины индуктивности

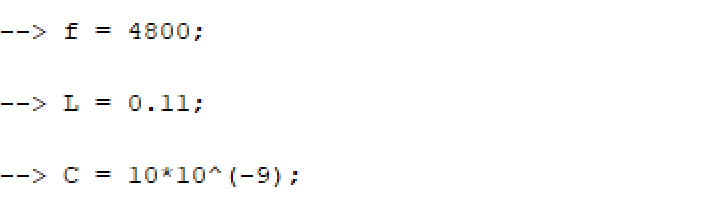
Рис. 1.2 Расчет величин при R = 160 Ом

Рис. 1.3 Расчет величин при R = 640 Ом

2. Расчет для гиратора

Рис. 2 Расчет для гиратора

3. Расчёт и построение графика зависимости входного сопротивления от частоты

Рис. 3.1 Расчёт зависимости входного сопротивления от частоты при R = 640 Ом

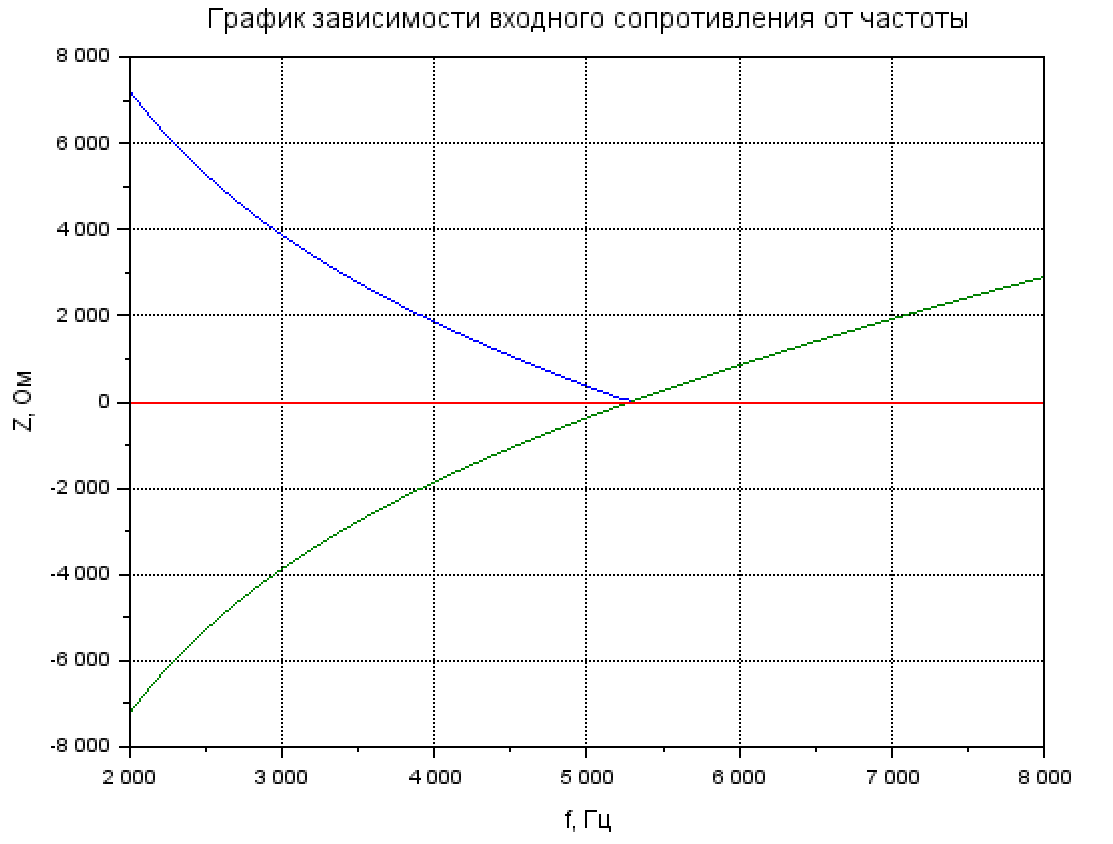
Рис. 3.2 График зависимости входного сопротивления от частоты при R = 640 Ом

Рис. 3.3 Расчёт зависимости входного сопротивления от частоты при R = 160 Ом

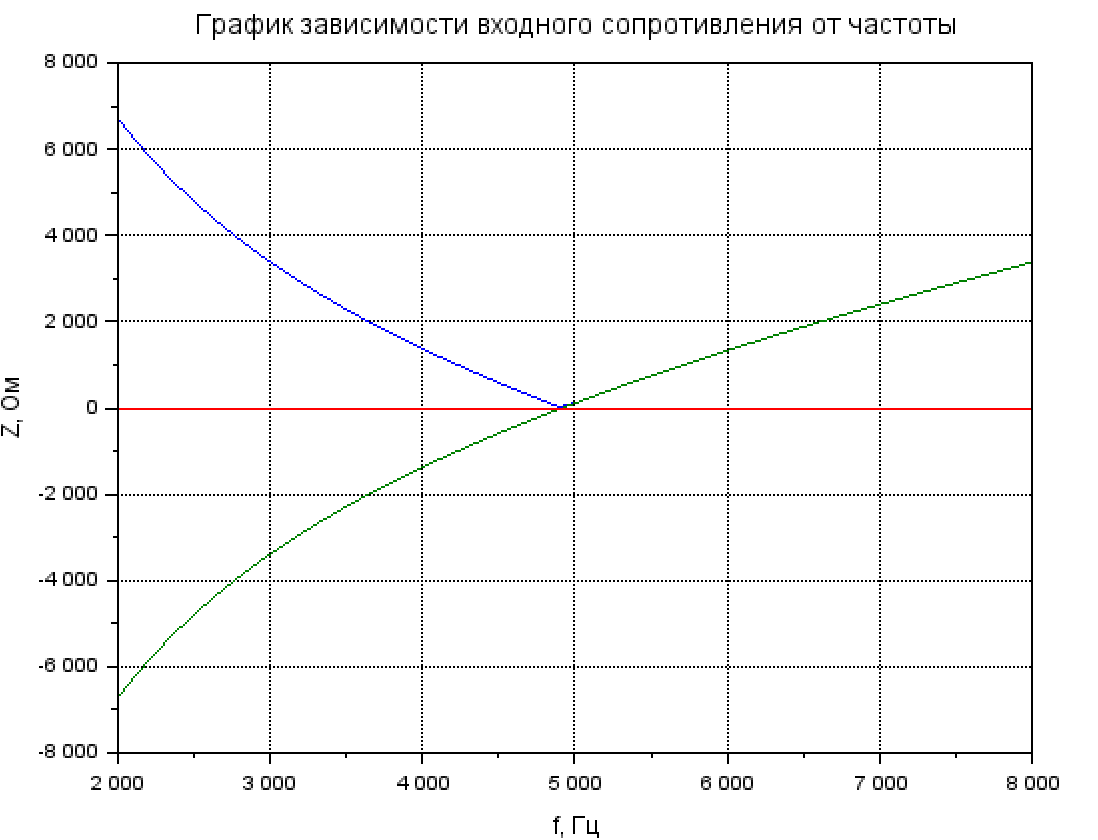
Рис. 3.4 График зависимости входного сопротивления от частоты при R = 160 Ом

4. Расчёт и построение графика зависимости фазы входного сопротивления от частоты

Рис. 4.1 Расчёт зависимости фазы входного сопротивления от частоты

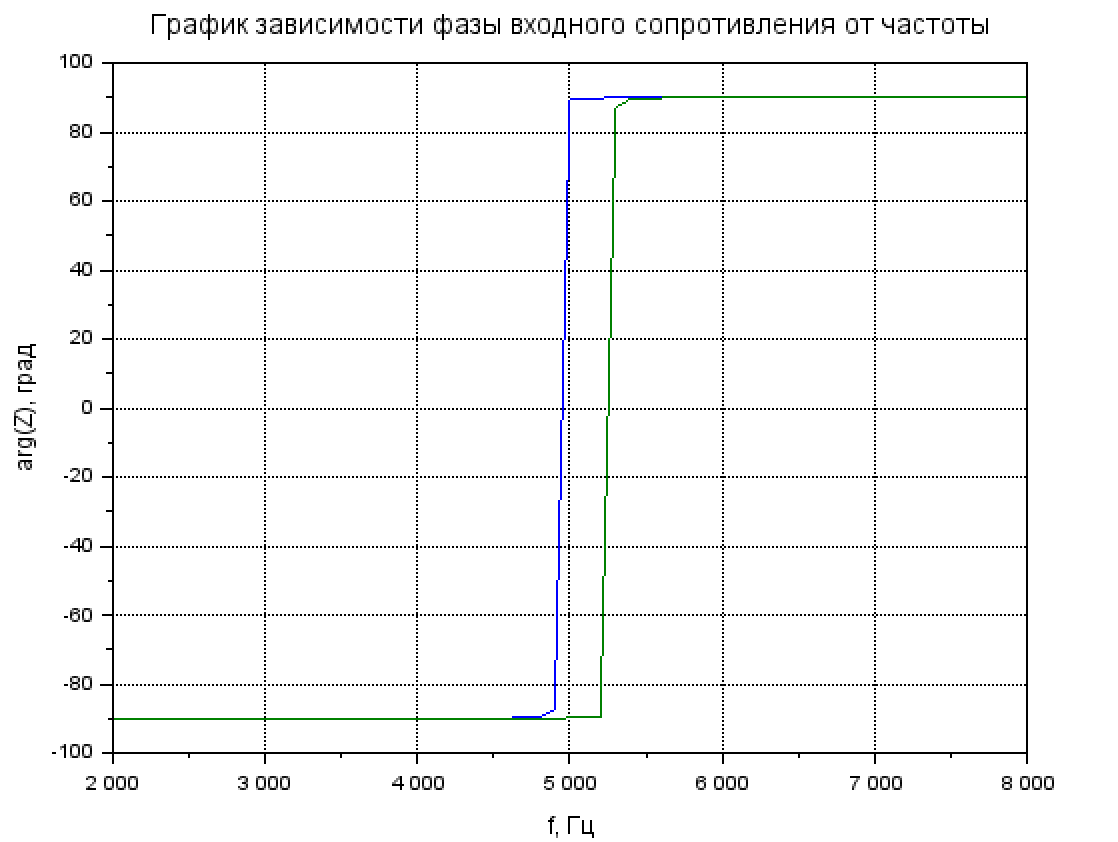
Рис. 4.2 График зависимости фазы входного сопротивления от частоты

5. Расчёт и построение графика зависимости входного тока от частоты

Рис. 5.1 Расчёт зависимости входного тока от частоты

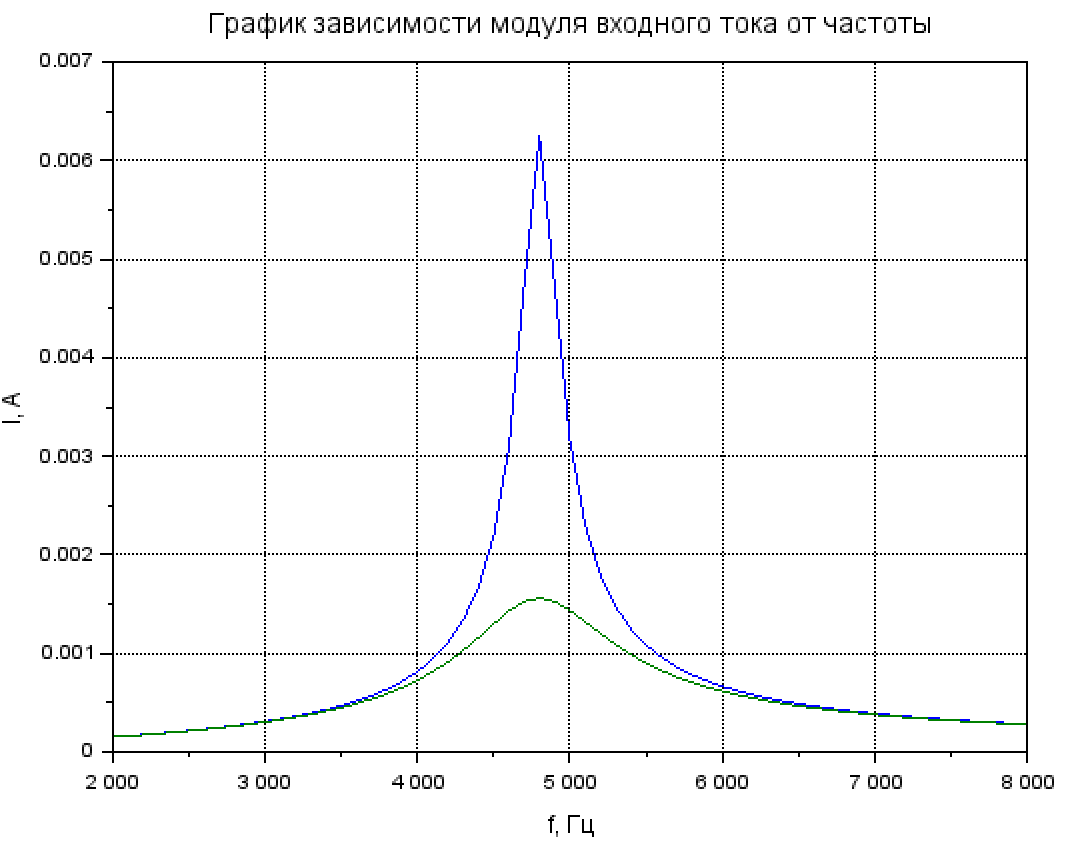
Рис. 5.2 График зависимости входного тока от частоты

Экспериментальное исследование

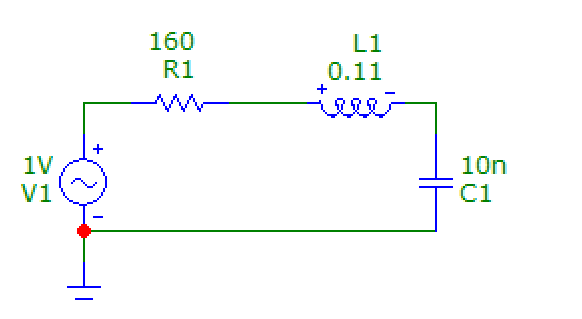
Рис. 6 Схема пассивного колебательного контура

1. Зависимость модуля входного сопротивления от частоты

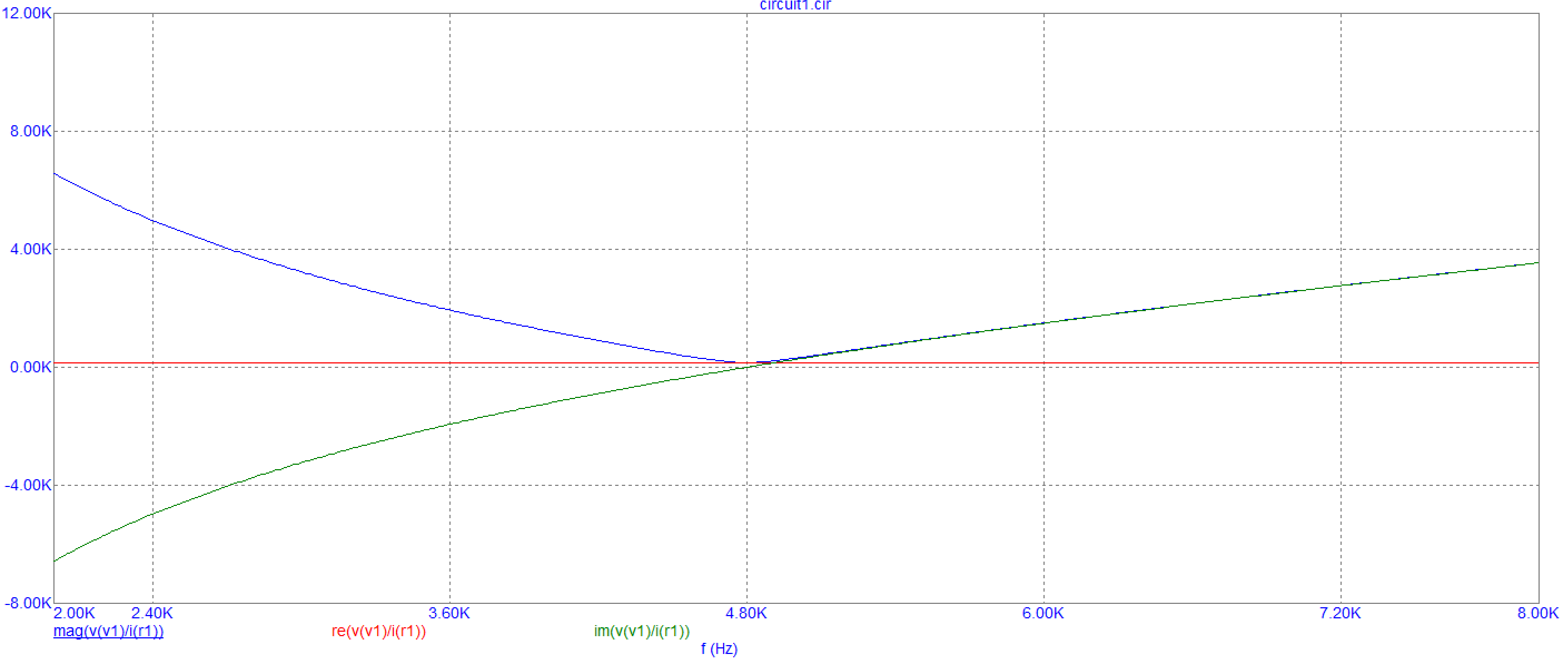
Рис. 6.1 График зависимости модуля входного сопротивления от частоты при R = 160 Ом

Вывод: при увеличении частоты до резонансной, входное сопротивление уменьшается, затем повышается.

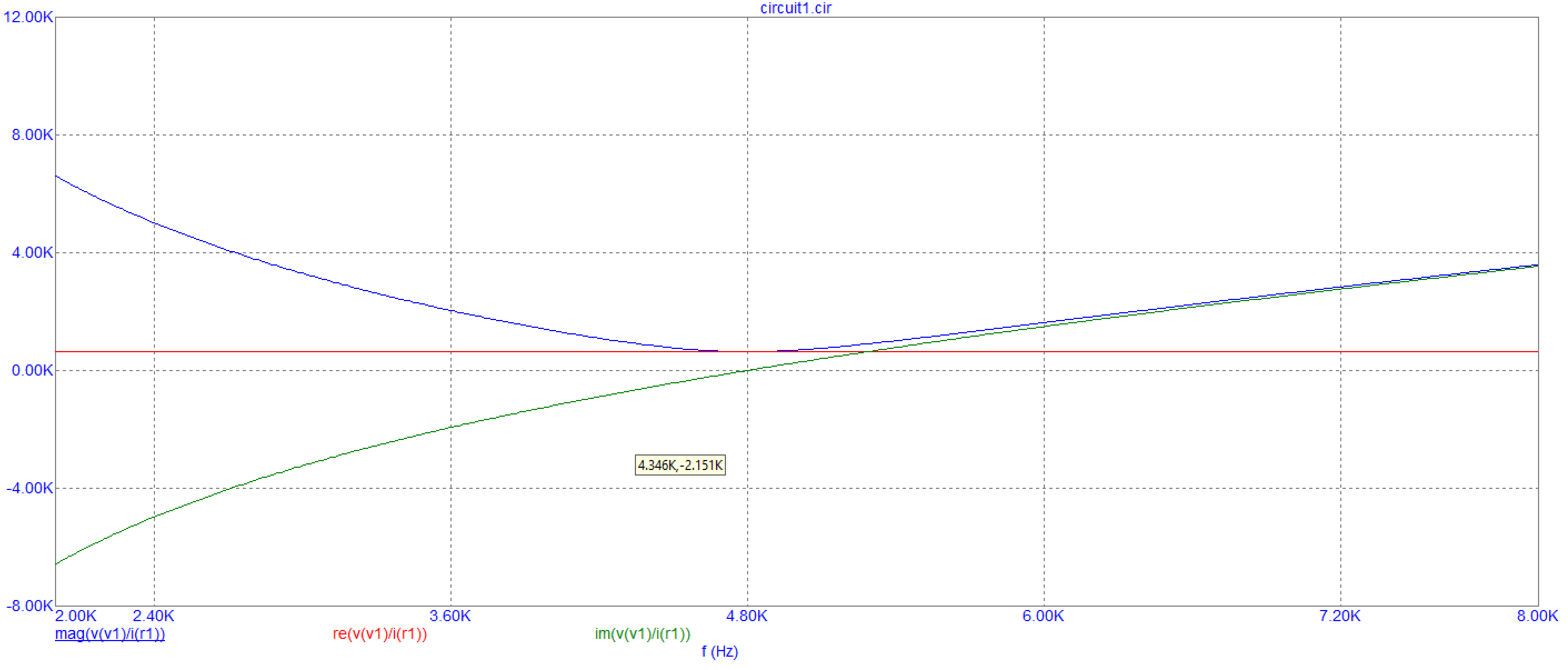
Рис. 6.2 График зависимости модуля входного сопротивления от частоты при R = 640 Ом

Вывод: при увеличении частоты до резонансной, входное сопротивление уменьшается, затем повышается.

2. Зависимость фазы входного сопротивления от частоты

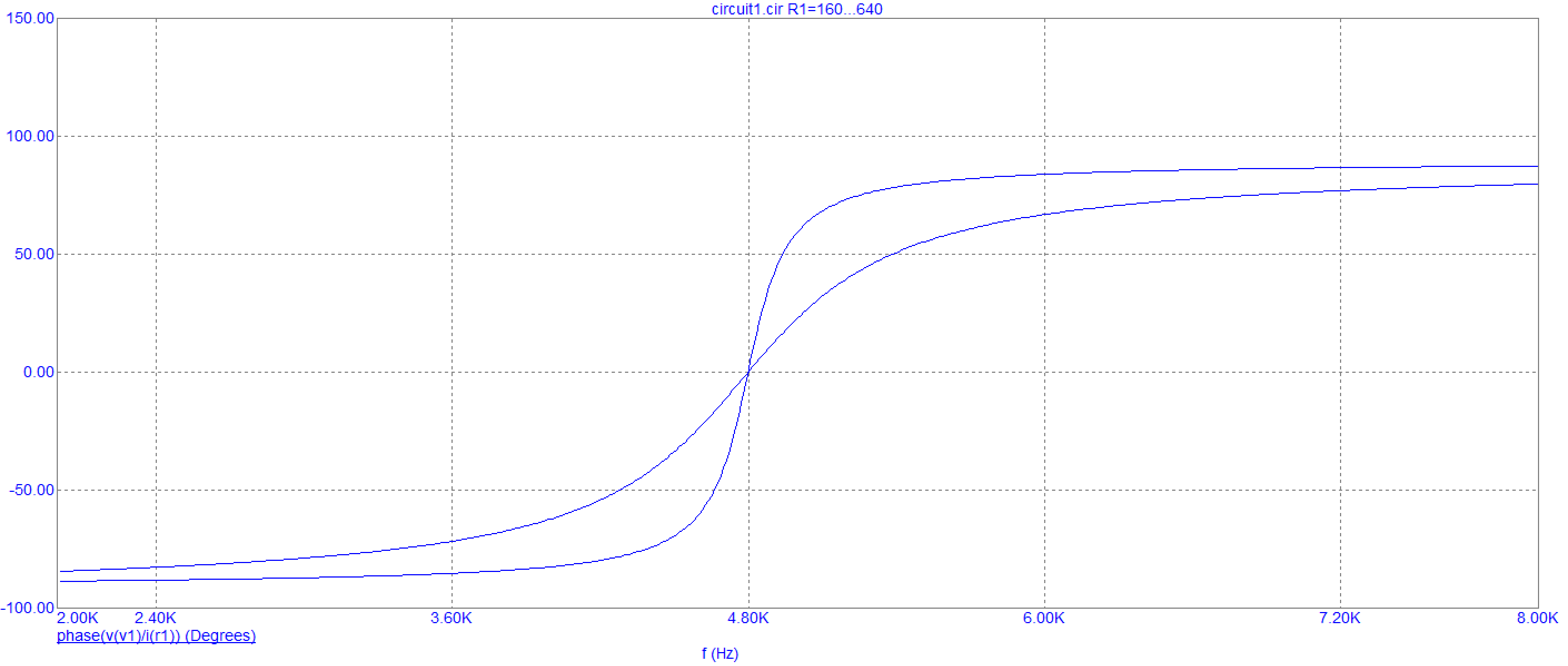
Рис. 7 График зависимости фазы входного сопротивления от частоты

Вывод: при увеличении частоты до резонансной, фаза входного сопротивления растет, затем уменьшается.

3. Зависимость модуля входного тока от частоты

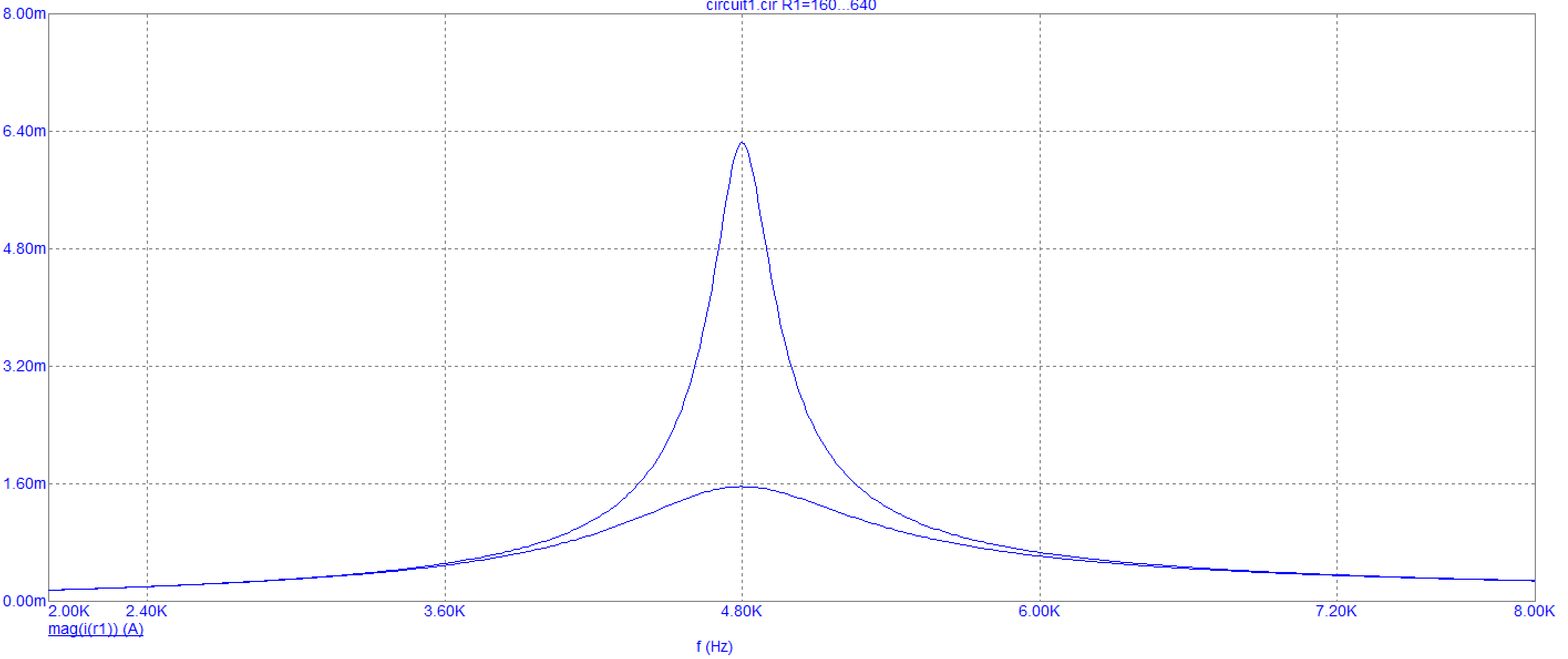
Рис. 8.1 График зависимости модуля входного тока от частоты

Вывод: при увеличении частоты модуль входного тока образует резонансную кривую с различной амплитудой в зависимости от резистора.

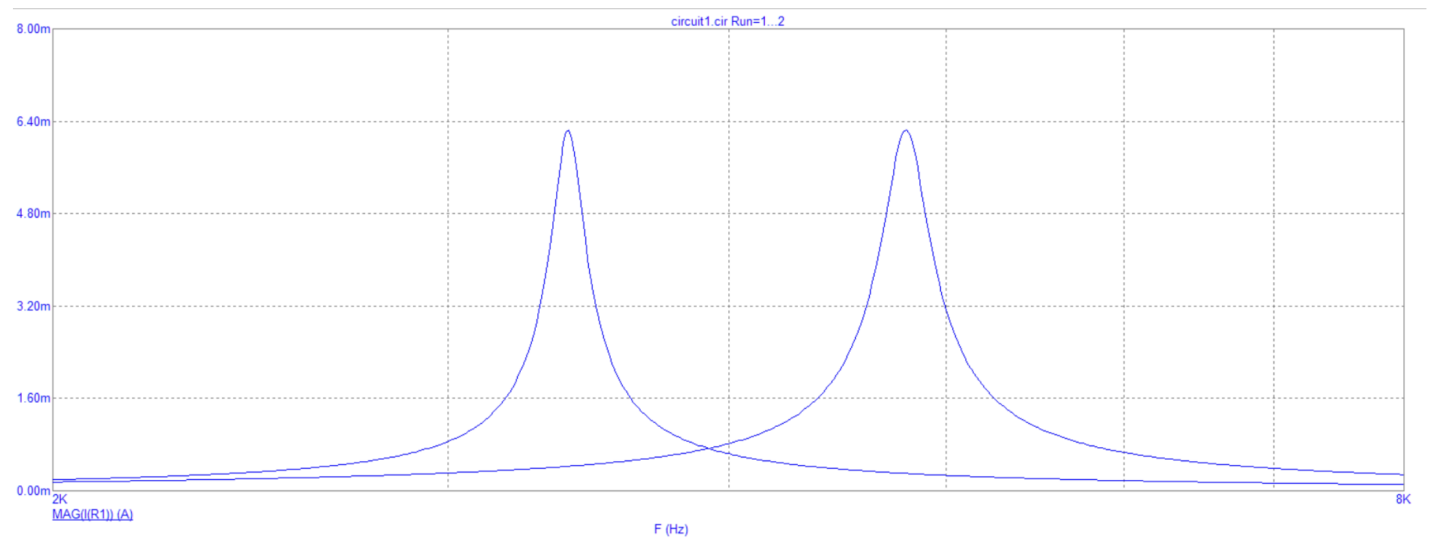
Рис. 8.2 График зависимости модуля входного тока от частоты при изменении параметров индуктивности

Вывод: при увеличении частоты модуль входного тока образует резонансные кривые с различной амплитудой в зависимости от индуктивности.

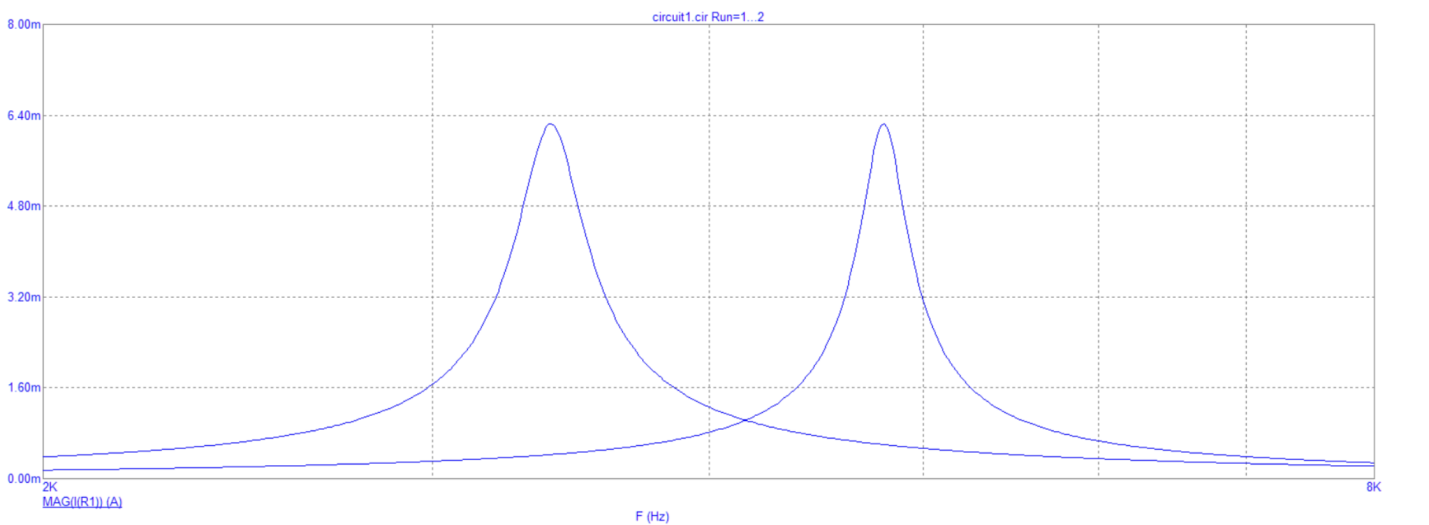Рис. 8.3 График зависимости модуля входного тока от частоты при изменении параметров емкости

Вывод: при увеличении частоты модуль входного тока образует резонансные кривые с различной амплитудой в зависимости от емкости.

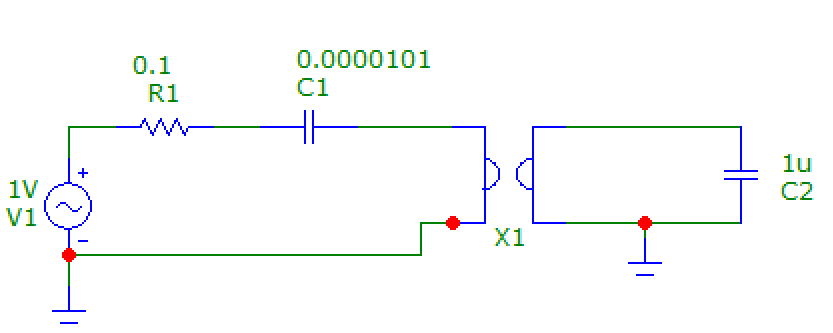
Рис. 9 Схема с гиратором

4. Зависимость модуля тока от частоты в схеме с гиратором

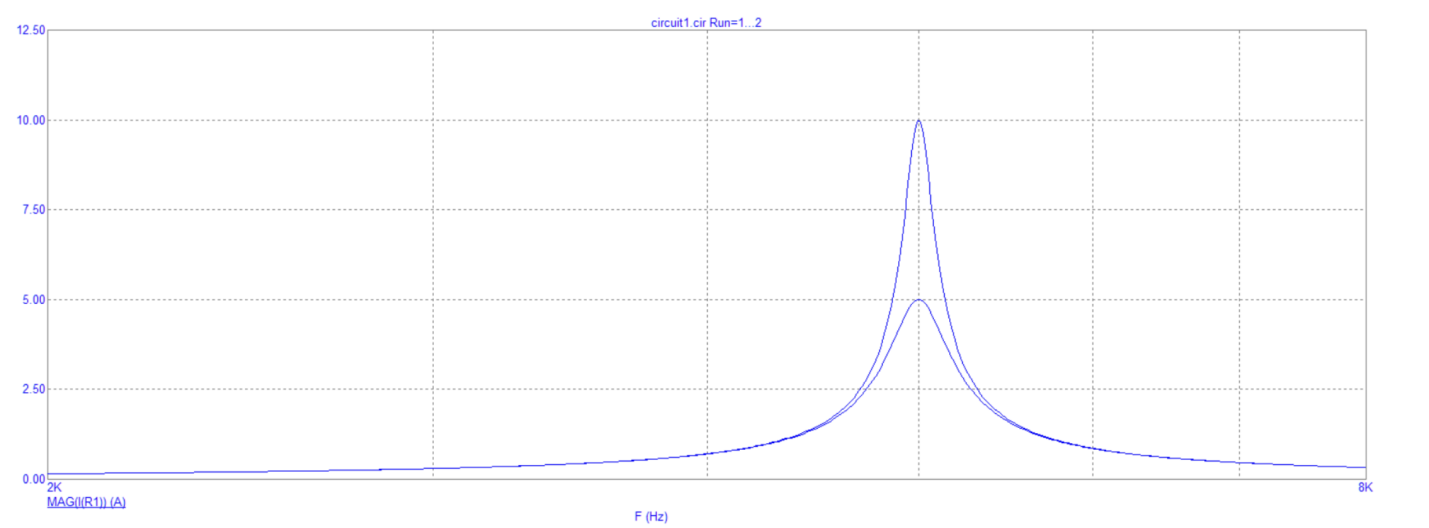
Рис. 10 График зависимости модуля входного тока от частоты в схеме с гиратором

Вывод: при увеличении частоты модуль входного тока образует резонансную кривую с различной амплитудой в зависимости от резистора.

Таблица 1 – результаты эксперимента

По предварительному расчету U1 = 1 B, f0 = 4,8 кГц, С = 10 нФ, L = 0,11 Гн										Получено экспериментально
R, Ом	, Ом	Q	f1, кГц	f2, кГц		П, кГц	I0, А	f0, кГц	f0, кГц		I0, А		f1, кГц	f2, кГц	П, кГц	Q
160	3316,6248	20,73	4,684	4,916		0,232	0,006	4,8	4,8		0,006		4,684	4,916	0,232	20,73
640	3316,6248	5,18	4,358	5,285		0,927	0,0015	4,8	4,8		0,0015		4,358	5,285	0,927	5,18
Гиратор
По предварительному расчету U1 = 1 B, f0 = 5 кГц, С2 = 1 мкФ, G = 0,1 См												Получено экспериментально
R, Ом					С1, мкФ							f0, кГц
0,1					10,14							5

Общий вывод: данные и графики, полученные в результате машинного эксперимента в программе Micro-Cap, полностью совпадают с данными и графиками, полученными в результате предварительного расчёта.

Практические задания и задачи к промежуточному контролю

1. Что такое входная функция и что такое передаточная функция цепи? Какова их физическая сущность?

Ответ: Под входной функцией обычно понимают зависимость входного комплексного сопротивления от частоты.

Под передаточной функцией обычно понимают зависимость комплексного коэффициента передачи по напряжению от частоты.

Физическая сущность входной функции заключается в определении величины и временной зависимости входного сигнала.

Передаточная функция показывает, как данная цепь передает гармонический сигнал той или иной частоты.

2. Дайте определение входной АЧХ, входной ФЧХ, передаточной АЧХ, передаточной ФЧХ цепи.

Ответ: Зависимость модуля входного комплексного сопротивления от частоты называют входной амплитудно-частотной характеристикой (входной АЧХ).

Зависимость аргумента входного комплексного сопротивления от частоты

называют входной фазочастотной характеристикой (входной ФЧХ).

Зависимость модуля входного комплексного коэффициента передачи от частоты называют передаточной амплитудно-частотной характеристикой (передаточной АЧХ).

Зависимость аргумента комплексного коэффициента передачи от частоты

называют передаточной фазочастотной характеристикой (передаточной ФЧХ).

3. Как, зная значение параметров элементов, рассчитать граничную частоту ƒ_гр для неразветвленной RL- и RC- цепи?

Ответ: По определению, граничная частота – частота, при которой вещественная часть входного комплексного сопротивления равна модулю его мнимой части:

Re[Z_вх(jω_гр )]=|Im[Z_вх(jω_гр )]|

Соответственно, нужно составить уравнение входной функции для заданной цепи.

Для RL-цепи это: Z_вх(jω)=R+jωL. Пользуясь предыдущей формулой составляем уравнение R=ω_гр L, где ω_гр – граничная частота, откуда ω_гр =R/L. ƒ_гр= ω_гр /2π.

Для RC-цепи это: Z_вх(jω)=R+1/jωC. Пользуясь той же формулой составляем уравнение R=1/ω_гр L, где ω_гр – граничная частота, откуда ω_гр =1/RC. ƒ_гр= ω_гр /2π.

4. На примерах схем RL- и RC- цепей, покажите, что в неразветвленной цепи первого порядка модуль входного комплексного сопротивления на граничной частоте равен R√2, а модуль аргумента входного комплексного сопротивления и модуль аргумента комплексного коэффициента передачи равны по 45° каждый.

Ответ: RL-цепь:

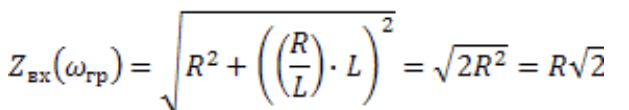
RC-цепь:

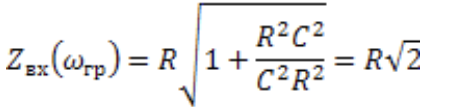
5. Как по графику входной АЧХ неразветвленной цепи первого порядка определить граничную частоту ƒгр?

Ответ: Как было показано в вопросе 4, при граничной частоте входная АЧХ равна R√2, следовательно, чтобы по графику определить граничную частоту, нужно найти точку, координата которой (ωгр; R√2).

6. Как по графику входной ФЧХ неразветвленной цепи первого порядка определить граничную частоту ƒгр?

Ответ: Нужно с помощь встроенной функции «Go to Y» на графике ФЧХ указать значение в 45º. В результате будет выделена точка, координата х которой и есть граничная частота.

7. Как по графику передаточной ФЧХ неразветвленной цепи первого порядка определить граничную частоту ƒгр?

Ответ: Нужно с помощь встроенной функции «Go to Y» на графике ФЧХ указать значение в 45º. В результате будет выделена точка, координата х которой и есть граничная частота.