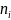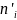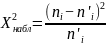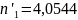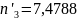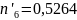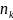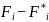Лабораторная работа №2

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра «Теория вероятности и прикладная математика»

Лабораторная работа №2

По дисциплине «Теория вероятностей и математическая статистика»

на тему

«Проверка статистических гипотез и теория оценивания»

Москва 2023

Задание 1

С помощью критериев согласия Пирсона и Колмогорова проверить гипотезу о том, что выборка из задания 2 лабораторной работы 1 имеет нормальное распределение.

Результаты вычислений

Проверка гипотезы о том, что выборка из задания 2 лабораторной работы 1 имеет нормальное распределение при помощи критерия согласия Пирсона.

Для проверки гипотезы о том, что выборка имеет нормальное распределение, с помощью критерия согласия Пирсона, необходимо определить теоретические частоты интервалов случайной величины Х.

Вероятность попадания случайной величины Х в заданный интервал (а; b) найдем по формуле:

=

=

=

=

=

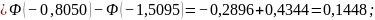
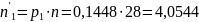
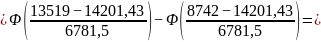
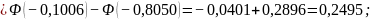
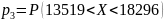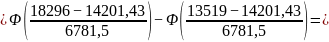
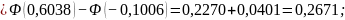
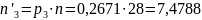
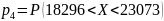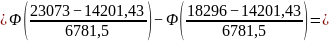
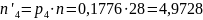
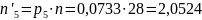
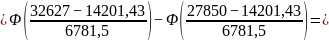
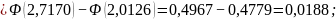
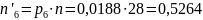
Таблица 1 – Результаты расчётов

№	Интервалы Наблюдаемых значений
1	[3965;8742)	6				0,9336
2	[8742;13519)	10				1,3003
3	[13519;18296)	5				0,8216
4	[18296;23073)	4	7		7,5516	0,0403
5	[23073;27850)	1
6	[27850;32627]	2

Число степеней свободы для распределения, которое описывается двумя параметрами равно k = r – 3 = 6 ‒ 3 = 3. Воспользуемся таблицей критических значений распределения X² Согласно уровню значимости α = 0,05 и найденному числу степеней свободы найдем критическое значение

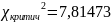. Так как 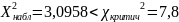, то нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение.

Проверка гипотезы о том, что выборка из задания 2 лабораторной работы 1 имеет нормальное распределение при помощи критерия согласия Колмогорова.

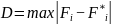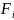Для того, чтобы применить критерий Колмогорова, необходимо подсчитать величину , где и 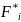и разности между ними представлены в таблице 2.

Таблица 2 – Результаты расчётов

1	6353,5	6		6	4,0544	1,9456	1,9456
2	11130,5	10		6+10=16	11,0404	4,9596	4,9596
3	15907,5	5		16+5=21	18,5192	2,4808	2,4808
4	20684,5	7		21+7=28	26,0708	1,9292	1,9292

Найдем наибольшее отклонение, затем вычислим значение критерия:

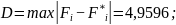
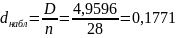
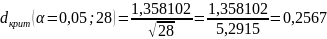
Так как 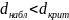, то гипотеза о нормальном законе распределения принимается.

Задание 2

Для выборки из задания 2 лабораторной работы 1 найти интервальные оценки параметров нормального распределения.

Результаты вычислений

Доверительный интервал для генерального среднего найдём по формуле:

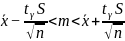
Определяем значение t_kp по таблицам функции Лапласа.

γ = 0,95; В этом случае 2Ф(t_kp) = γ

Ф(t_kp) = γ/2 = 0,95/2 = 0,475;

По таблице функции Лапласа найдем, при каком t_kp значение Ф(t_kp) = 0,475 t_kp(γ) = (0,475) = 1,96.

Предельная ошибка выборки:

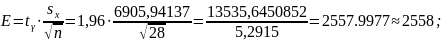
Получаем доверительный интервал с надежностью γ = 0,95:

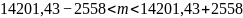
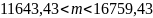
Доверительный интервал для среднеквадратического отклонения

S(1-q) < σ < S(1+q)

Найдем доверительный интервал для среднеквадратического отклонения с надежностью γ = 0,95 и объему выборки n = 28. По таблице q = q(γ ; n) определяем параметр q(0,95;28) = 0,28.

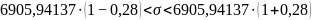
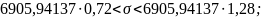
Таким образом, интервал ) покрывает параметр σ с надежностью γ = 0,95.

Доверительный интервал для дисперсии

По таблице находим два значения для доверительной вероятности с числом степеней свободы

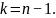
Поскольку доверительная вероятность равна 95%, тогда α = 1 – 0,95 = 0,05.

Число степеней свободы k = n – 1 = 27.

По таблице находим два χ2 значения для 0,95 и 0,05.

Значения находятся по таблицам распределения, исходя из следующих условий:

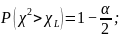
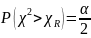
Найдём эти значения

.

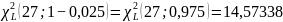Тогда:

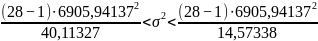
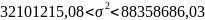
Вывод

В данной лабораторной работе были рассмотрены основные понятия и методы проверки статистических гипотез и теории оценивания. Удалось поработать с критериями согласия Пирсона и Колмогорова, а также с помощью них доказать гипотезу о виде теоретического закона распределения генеральной совокупности. Во втором задании удалось найти интервальные оценки параметров нормального распределения.

В результате были получены навыки по проверке статистических гипотез и оцениванию параметров распределения.