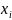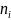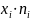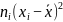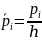Лабораторная работа №1
.docxМинистерство цифрового развития, связи и массовых коммуникаций Российской Федерации
Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Кафедра «Теория вероятности и прикладная математика»
Лабораторная работа №1
По дисциплине «Теория вероятностей и математическая статистика»
на тему
«Описательная статистика»
Москва 2023
Задание 1
По предложенной выборке дискретной генеральной совокупности, содержащей рейтинг группы студентов, построить вариационный ряд, найти объем выборки, интервал варьирования, размах выборки, построить статистический ряд распределения, эмпирическую функцию распределений, вычислить основные описательные статистики: выборочное среднее, выборочные смещенную и несмещенную дисперсию и среднеквадратическое отклонение, выборочную моду, выборочную медиану, нижнюю и верхнюю квартиль. Построить полигон частот, график эмпирической функции распределения и «ящик с усами».
Задание 2
По предложенной выборке непрерывной генеральной совокупности, содержащей показатели работы предприятий, построить вариационный ряд, найти объем выборки, интервал варьирования, размах выборки, выполнить группировку данных, построить гистограмму распределения, эмпирическую функцию распределения, вычислить основные описательные статистики: выборочное среднее, выборочные смещенную и несмещенную дисперсию и среднеквадратическое отклонение, выборочную моду, по не группированным данным найти выборочную медиану, нижнюю и верхнюю квартиль. Построить гистограмму, график эмпирической функции распределения и «ящик с усами».
![]()

Задание 1
Вариационный ряд: 0 0 0 1 2 2 2 3 3 3 3 4 6 7 7 8 8 9 9 9
Объем выборки: n = 20
Интервал варьирования: [0; 9]
Размах выборки: R = 9
Статистический ряд распределения:
|
0 |
1 |
2 |
3 |
4 |
6 |
7 |
8 |
9 |
|
3 |
1 |
3 |
4 |
1 |
1 |
2 |
2 |
3 |
Эмпирическая функция распределений:
|
0 |
1 |
2 |
3 |
4 |
6 |
7 |
8 |
9 |
|
3 |
1 |
3 |
4 |
1 |
1 |
2 |
2 |
3 |
|
0,15 |
0,2 |
0,35 |
0,55 |
0,6 |
0,65 |
0,75 |
0,85 |
1 |
|
0,15 |
0,05 |
0,15 |
0,2 |
0,05 |
0,05 |
0,1 |
0,1 |
0,15 |

График эмпирической функции распределения (рис. 1):
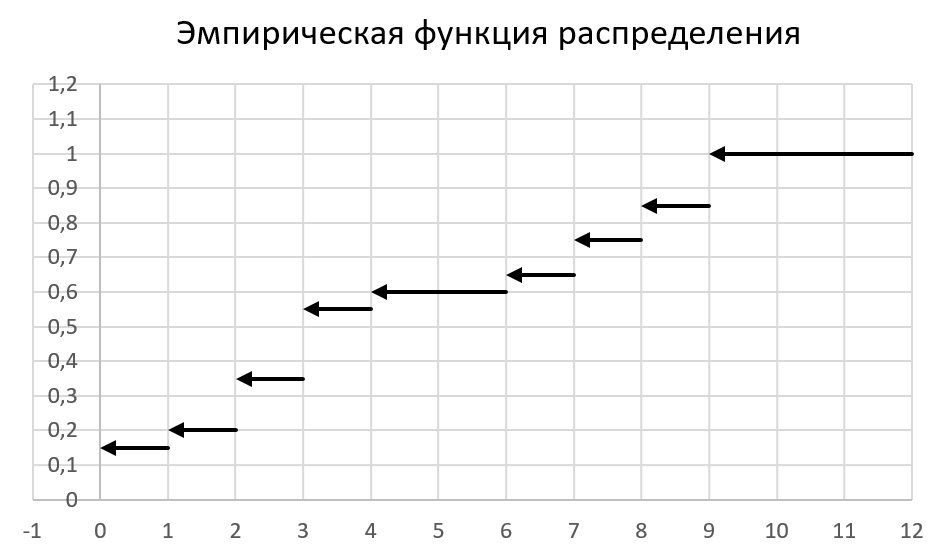
Рисунок 1 - Эмпирическая функция распределения
Основные описательные статистики:
Таблица 1 – Расчётная таблица
|
Количество значений |
|
|
0 |
3 |
0 |
55,47 |
1 |
1 |
1 |
10,89 |
2 |
3 |
6 |
15,87 |
3 |
4 |
2 |
6,76 |
4 |
1 |
4 |
0,09 |
6 |
1 |
6 |
2,89 |
7 |
2 |
14 |
14,58 |
8 |
2 |
16 |
27,38 |
9 |
3 |
27 |
66,27 |
Итого: |
20 |
86 |
200,2 |
Выборочное среднее:
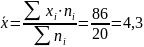
Выборочная смещённая дисперсия:

Выборочное смещённое среднеквадратическое отклонение:
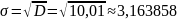
Выборочная несмещённая дисперсия:

Выборочное несмещённое среднеквадратическое отклонение:
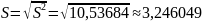
Выборочная мода:
М0 = 3 (так как в данной совокупности встречается n = 4 раз)
Выборочная медиана:

Нижняя квартиль:

Верхняя квартиль:
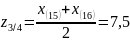
«Ящик с усами»:
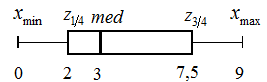
Полигон частот (рис. 2):

Рисунок 2 - Полигон частот
Результаты выполнения в Excel (рис. 3-4):
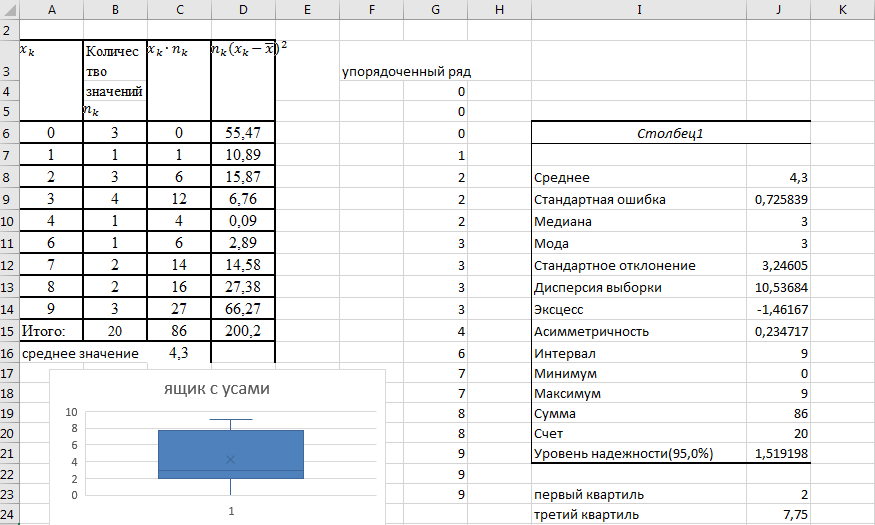
Рисунок 3 – Результаты выполнения в Excel
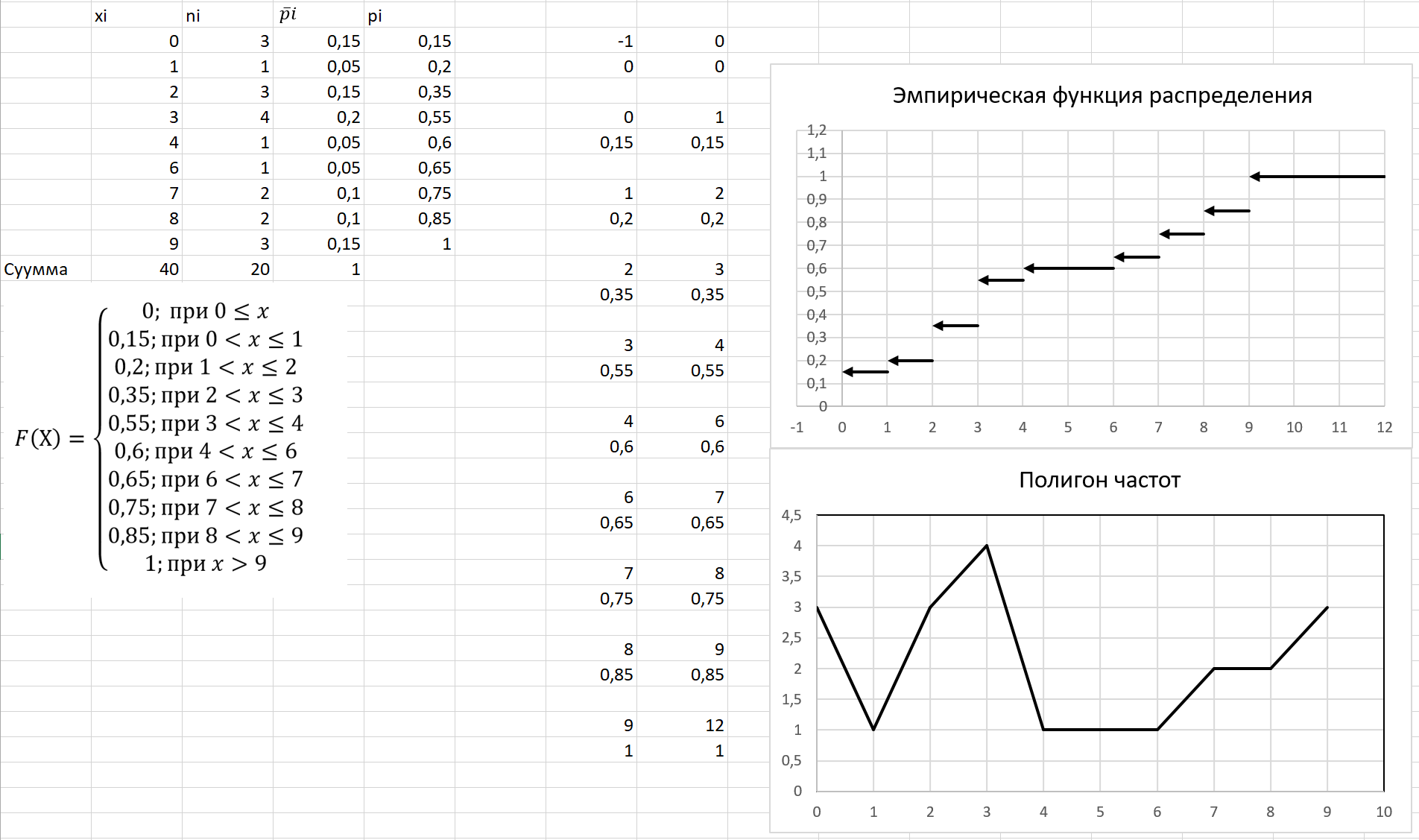
Рисунок 4 – Результаты выполнения в Excel
Задание 2
Вариационный ряд: 3967, 6265, 6391, 6462, 6555, 8402, 8810, 8901, 9166, 9185, 9484, 10342, 11085, 11115, 11429, 11470, 13833, 15118, 15283, 17478, 17659, 18963, 19418, 19448, 20874, 24628, 31160, 32625, 46461, 49727.
Выборочная медиана:
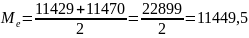
Нижняя квартиль:
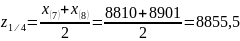
Верхняя квартиль:
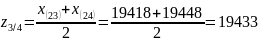
Построив «Ящик с усами» (рис. 5), мы определили два аномальных значения, которые нужно исключить из совокупности - это значения 46461 и 49727. Так как если составлять ряд с данными показателями, то некоторые интервалы остаются незаполненными, то есть в некоторые интервалы не попадает ни одна единица совокупности.
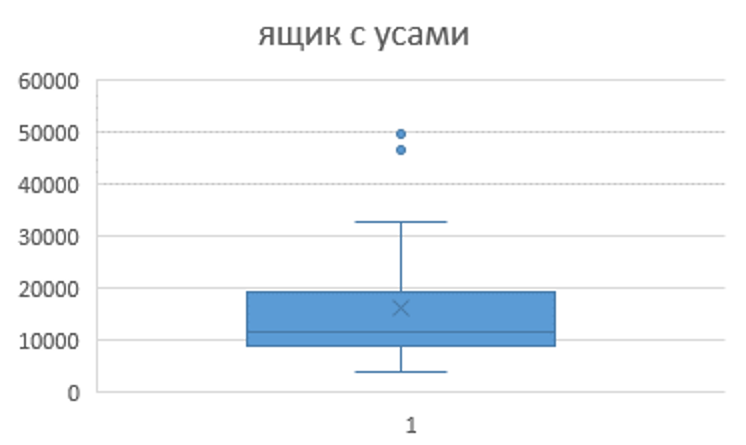
Рисунок 5 – «Ящик с усами»
Объем выборки: n = 28
Интервал варьирования: [3967; 32625]
Размах выборки: R = 28658
Группировка данных:

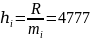
Получим интервалы: 3965 - 8742 - 13519 - 18296 - 23073 - 27850 – 32627
Таблица 2 - Интервальный статистический ряд распределения X
№ п/п |
Интервалы |
|
|
|
Середина интервала
|
1 |
[3965;8742) |
6 |
0,214 |
0,00004486 |
6353,5 |
2 |
[8742;13519) |
10 |
0,357 |
0,00007476 |
11130,5 |
3 |
[13519;18296) |
5 |
0,179 |
0,00003738 |
15907,5 |
4 |
[18296;23073) |
4 |
0,143 |
0,00002991 |
20684,5 |
5 |
[23073;27850) |
1 |
0,036 |
0,000007476 |
25461,5 |
6 |
[27850;32627] |
2 |
0,071 |
0,00001495 |
30238,5 |
Гистограмма распределения (рис. 6):
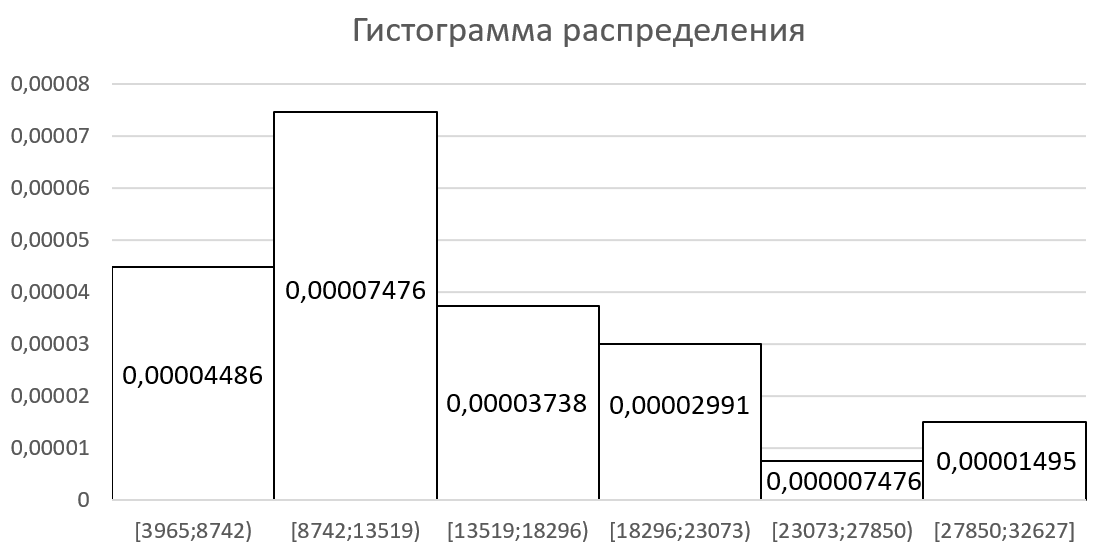
Рисунок 6 - Гистограмма распределения
Эмпирическая функция распределения:

Основные описательные статистики:
Таблица 3 – Расчетная таблица
№ п/п |
Интервалы
|
Середина интервала |
|
|
|
1 |
[3965;8742) |
6353,5 |
6 |
38121 |
369539897,2 |
2 |
[8742;13519) |
11130,5 |
10 |
111305 |
94306022,9 |
3 |
[13519;18296) |
15907,5 |
5 |
79537,5 |
14553398,6 |
4 |
[18296;23073) |
20684,5 |
4 |
82738 |
168120860,6 |
5 |
[23073;27850) |
25461,5 |
1 |
25461,5 |
126789208,6 |
6 |
[27850;32627] |
30238,5 |
2 |
60477 |
514375320,0 |
Выборочное среднее:
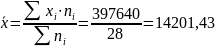
Выборочная смещённая дисперсия:
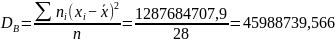
Выборочная несмещённая дисперсия:
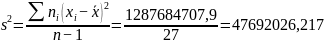
Выборочное несмещённое среднеквадратическое отклонение:
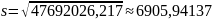
Выборочное среднеквадратическое отклонение:

Мода:
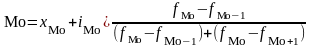 ,
,
где
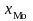 – нижняя граница модального интервала;
– нижняя граница модального интервала;
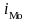 – величина
модального интервала;
– величина
модального интервала;
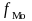 – частота модального
интервала;
– частота модального
интервала;
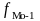 – частота интервала,
предшествующего модальному;
– частота интервала,
предшествующего модальному;
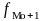 – частота интервала,
следующего за модальным.
– частота интервала,
следующего за модальным.
Модальным является интервал [8742;13519).


График эмпирической функции распределения (рис. 7):
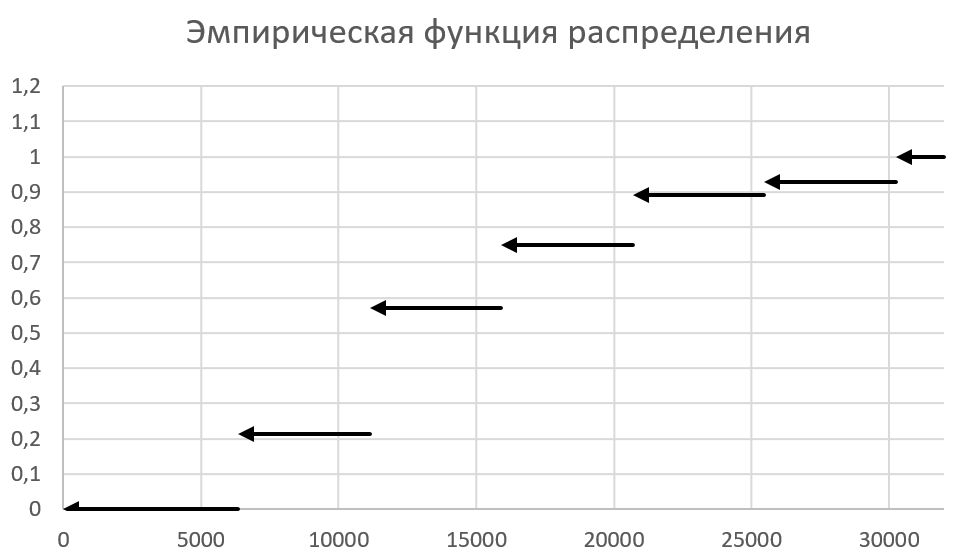
Рисунок 7 - Эмпирическая функция распределения
Результаты выполнения в Excel (рис. 8-10):
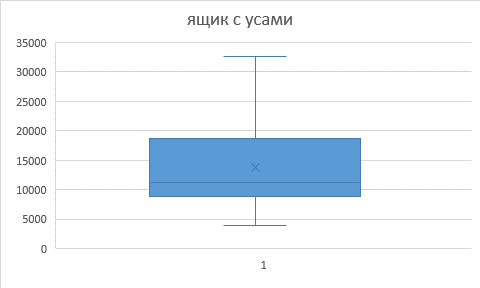
Рисунок 8 – «Ящик с усами»

Рисунок 9 – Результаты выполнения в Excel
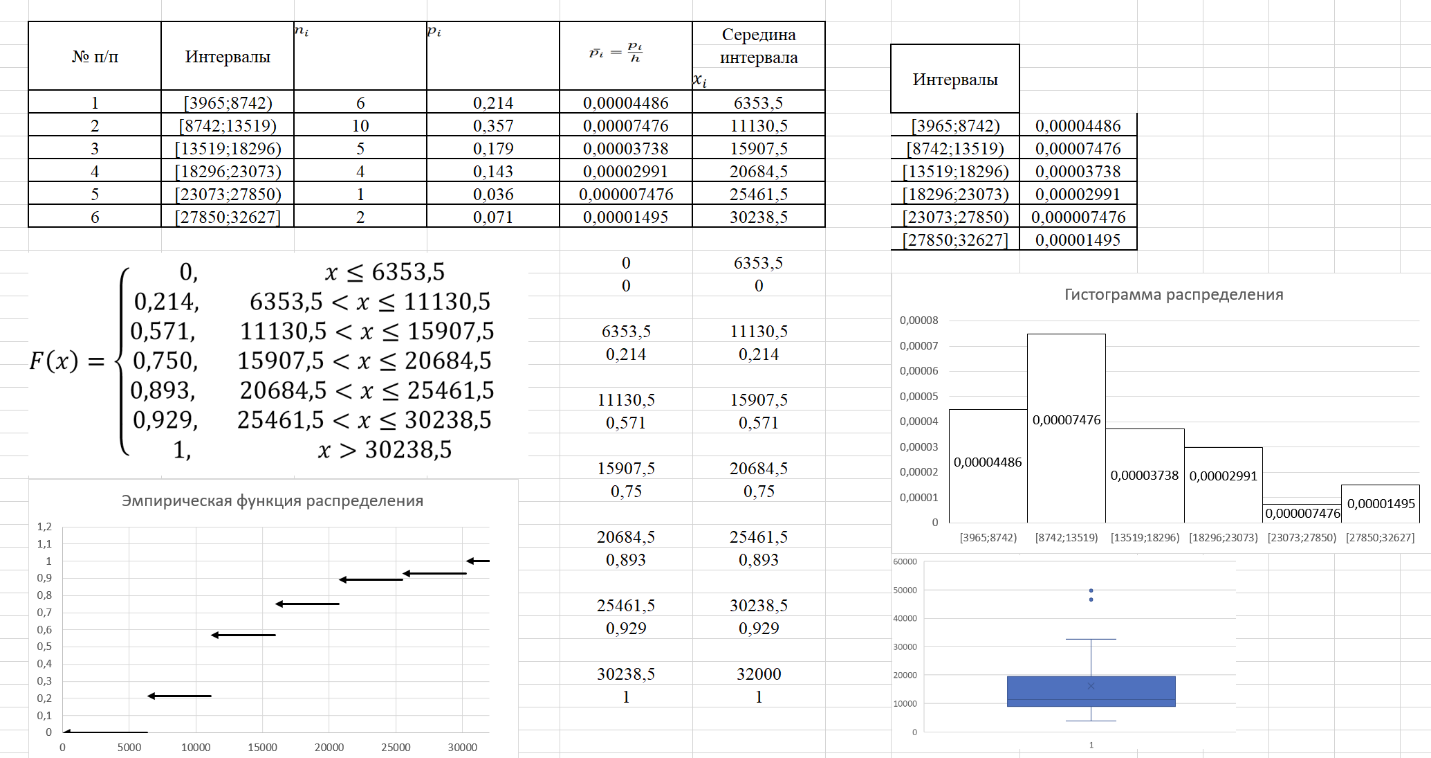
Рисунок 10 – Результаты выполнения в Excel
Вывод
В ходе выполнения лабораторной работы, мною были выполнены задания по расчёту различных описательных статистик, а также характеристик на основе различных выборок. Также удалось поработать с двумя типами выборок и использовать различные методы нахождения их характеристик. В ходе работы ещё были построены различные графики, отражающие вычисленные результаты.