МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра САПР

отчет

по лабораторной работе №1

по дисциплине «Алгоритмы и Структуры Данных»

Тема: «Алгоритмы сжатия без потерь»

Студентка гр. 3352
Преподаватель

Санкт-Петербург

2025

Цель работы:

Реализовать алгоритмы сжатия и выявить наилучший компрессор для выбранных файлов.

Задачи:

• Реализовать алгоритмы: HA, BWT, MTF, RLE, LZ77, LZ78. Описать данные алгоритмы и выявить их пространственную и временную сложности.

• Исследовать зависимость энтропии от размера блоков, на которые разбивается текст, подаваемый на вход BWT+MTF, для enwik7. Вывести полученные результаты на график и сделать вывод об оптимальном размере блока.

• Исследовать зависимость коэффициента сжатия от размера буфера для алгоритма LZ77. Вывести полученные результаты на график и сделать вывод об оптимальном размере буфера.

• Собрать на основе реализованных алгоритмов следующие компрессоры:

1. HA

2. Run-length encoding (RLE)

3. BWT + RLE

4. BWT + MTF + HA

5. BWT + MTF + RLE + HA

6. LZ77

7. LZ77 + HA

8. LZ78

9. LZ78 + HA

• Удостовериться в корректной компрессии и декомпрессии данных.

• Исследовать эффективность компрессоров для всех тестовых данных.

• Свести результаты в виде коэффициента сжатия для каждого компрессора и всех тестовых данных в таблицы. В таблице указать размер до компрессии, после компрессии и после декомпрессии в байтах, коэффициент сжатия. Коэффициент сжатия округлить до трех цифр после запятой.

Теоретическая часть

RLE - Run-Length Encoding

Простой метод сжатия информации, который заменяет последовательность одинаковых элементов на пару “количество одинаковых последовательных элементов - элемент”.

Работа алгоритма: 

Шаг 1: Проход по всем элементам с нахождением одинаковых последовательностей.

Шаг 2: Кодирование, состоящее из пары: символ - его количество.

Шаг 3: Вывод полученной строки.

Пример:

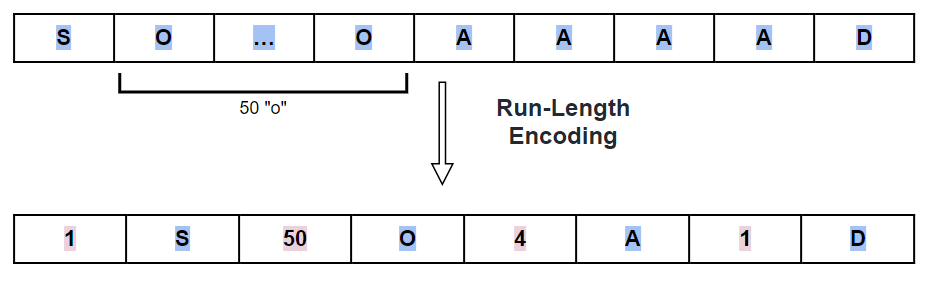
Декодирование:

Символы последовательно записываются то количество раз, которое представлено в закодированном виде.

Пространственная сложность:

Алгоритм требует линейное пространство, так как требуется сохранить информацию о каждом символе и количестве его повторений.

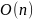, где n - количество символов.

Временная сложность: 

Алгоритм является линейным, так как совершается один проход по всему массиву.

, где n – количество символов.

MTF - Move-To-Front

Алгоритм кодирования для предварительной обработки данных, работающий по принципу “движение к началу”. Служит для улучшения эффективности кодирования.

Работа алгоритма:

Шаг 1: Каждому значению байта принадлежит ячейка с номером, равная его значению (0,1,2,…,255). Из этого составляется список – алфавит.

Шаг 2: Выполняется проход по массиву символов. На выход подается номер элемента с данным значением.

Шаг 3: Пройденный символ перемещается в начало списка. Остальные элементы смещаются вправо на 1 символ. Алфавит принимает новый вид.

Шаги 2 – 3 повторяются до последнего символа из строки данных.

Шаг 4: Вывод полученной строки.

пример:

Входная строка: BACABCC

Закодированная строка: 1121220

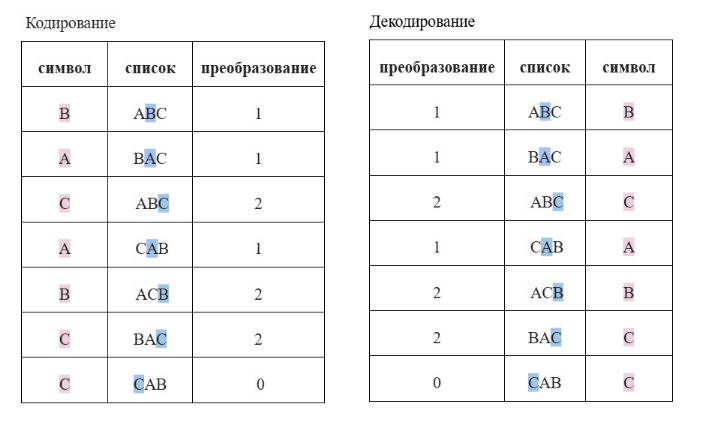
Декодирование:

Происходит по аналогичному алгоритму, опираясь на номер нужного символа и помещая его в начало алфавита.

пространственная сложность:

Алгоритм хранит список символов, включающий все уникальные.

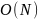, где N – количество уникальных символов в строке

временная сложность:

Необходимость поиска и перемещения символов приводят к сложности:

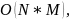
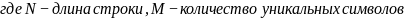
 BWT - Burrows-Wheeler transform

Алгоритм, оперирующий блоками данных с заранее определенным составом элементов.

Работа алгоритма:

Шаг 1: Создание всех возможных циклических сдвигов.

Шаг 2: Сортировка всех циклических сдвигов в лексикографическом порядке.

Шаг 3: Формирование выходной строки из последнего символа каждого сдвига.

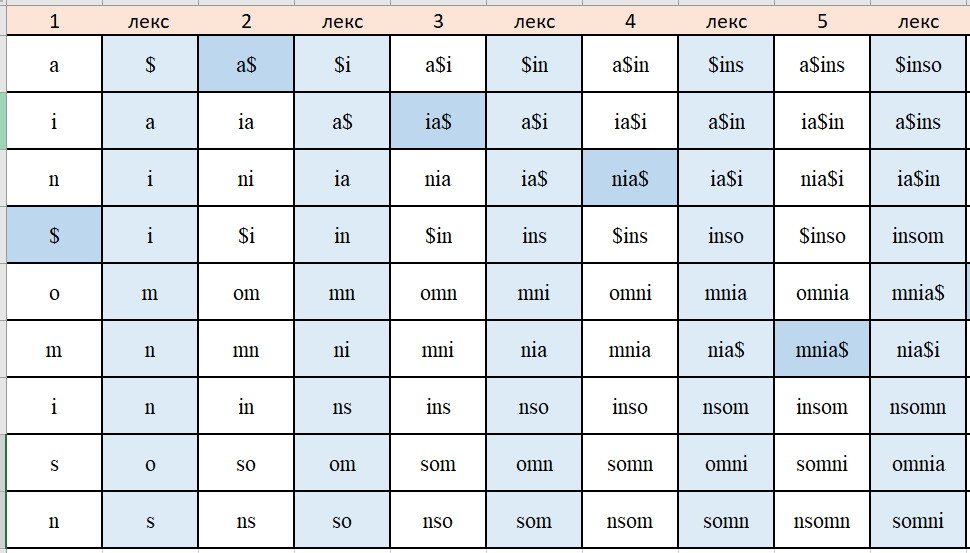
Пример:

Входная строка: insomnia$

циклический сдвиг	лексикографичеcкий порядок	последний символ
insomnia$	$insomnia	a
$insomnia	a$insomni	i
a$insomni	ia$insomn	n
ia$insomn	insomnia$	$
nia$insom	mnia$inso	o
mnia$inso	nia$insom	m
omnia$ins	nsomnia$i	i
somnia$in	omnia$ins	s
nsomnia$i	somnia$in	n

Закодированная строка: ain$omisn

Декодирование:

Шаг 1: Выписывается столбец закодированного сообщения.

Шаг 2: Данный столбец сортируется в лексикографическом порядке.

Шаг 3: К каждой строке слева дописывается символ из закодированной строки. Все остальные символы сдвигаются на 1 вправо.

Шаги 2- 3 повторяются до начальной длины сообщения.

Пространственная сложность:

Для хранения всех циклических сдвигов и их сортировки требующаяся память:

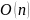, где n – длина строки

Временная сложность:

Сложность складывается из создания и сортировки всех циклических сдвигов. Так как используется алгоритм, работающий с блоками, каждый блок требует О(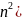 на создание всех циклических сдвигов и O(n^2log(n)) на их сортировку. Объединив работу всех блоков вместе (их N/n, где N – длина сообщения и n – длина блока), получаем:

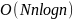
 HA - Huffman coding

Метод сжатия данных без потерь, основанный на кодировании данных длиной кода в зависимости от частоты появления символов в сообщении.

Работа алгоритма:

Шаг 1: Проход по входным данным с подсчетом количества вхождений каждого символа.

Шаг 2: Создание узлов, каждый из которых содержит информацию о самом символе и его частоте в тексте.

Шаг 3: Построение дерева начиная с двух узлов с наименьшими частотами. Новый узел – - родительский с суммой частот двух дочерних узлов.

Шаг 4: После того, как дерево построено, левым ребрам присваивается 0, правым 1. Исходя из данных значений составляются коды Хаффмана для всех символов.

Пример:

Кодируемое слово: successes

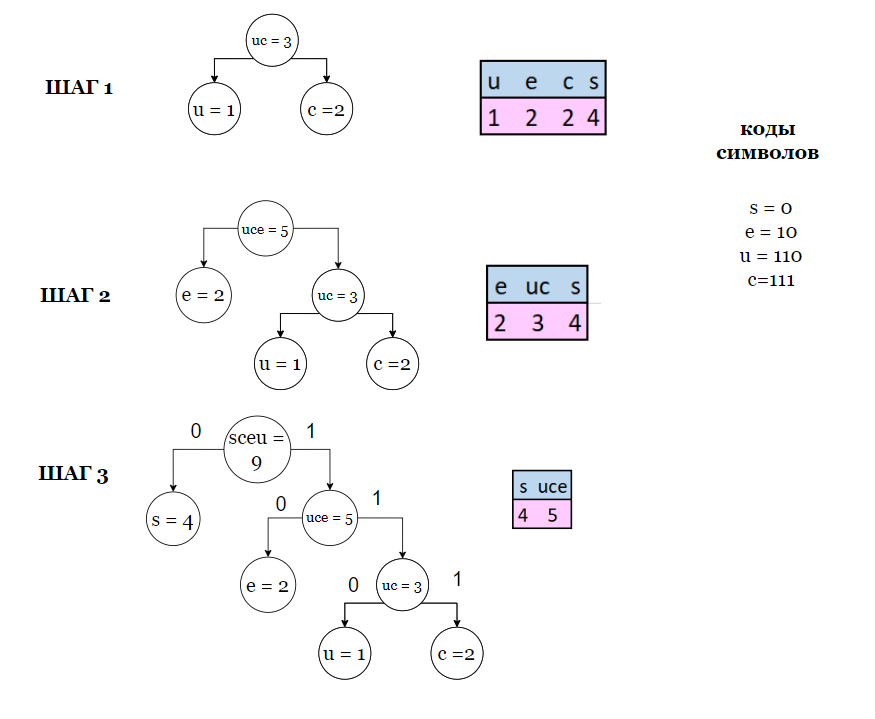
Декодирование:

Декодирование происходит по ходу следования по дереву Хаффмана, двигаясь с корня до листа с символом.

Пространственная сложность:

Построение дерева Хаффмана: использует пространство для хранения узла и приоритета очереди.

,

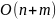где n – количество уникальных символов входных данных

m - длина исходных данных

Кодирование и декодирование: хранение сообщения.

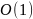
Временная сложность:

Построение дерева Хаффмана:

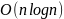, где n – количество уникальных символов

Обход при дерева декодировании:

, где n – количество битов закодированного сообщения

LZ77 - Lempel-Ziv 1977

Метод сжатия без потерь, использующий технику поиска повторяющихся последовательностей данных.

Работа алгоритма:

Шаг 1: Инициализация окна, исходя из которого будет происходить поиск символов.

Шаг 2: Чтение входных данных, начиная с первого символа.

Шаг 3: Для каждого символа проводится поиск наибольшей последовательности, встречающейся до этого в пределах заданного окна на шаге 1.

Шаг 4: Сравнение текущей позиции и с предыдущими символами в окне для поиска максимальной длины совпадения. Запоминание этой длины и позицию ее начала.

Шаг 5: Сдвиг окна на длину совпадения +1.

Повторение шагов 3-5.

Пример:

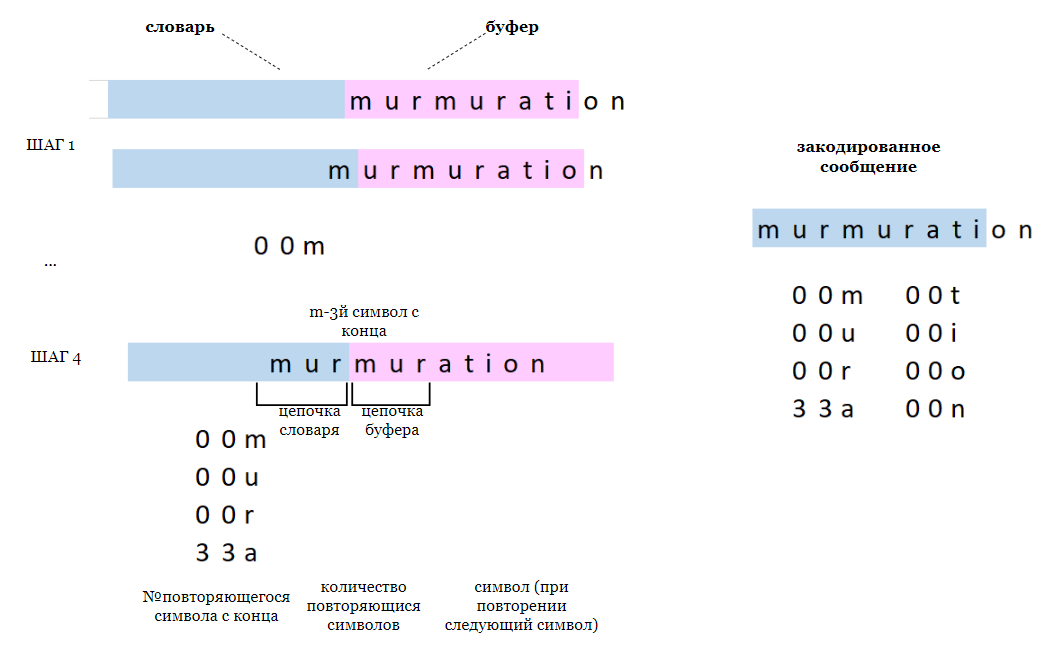
Декодирование:

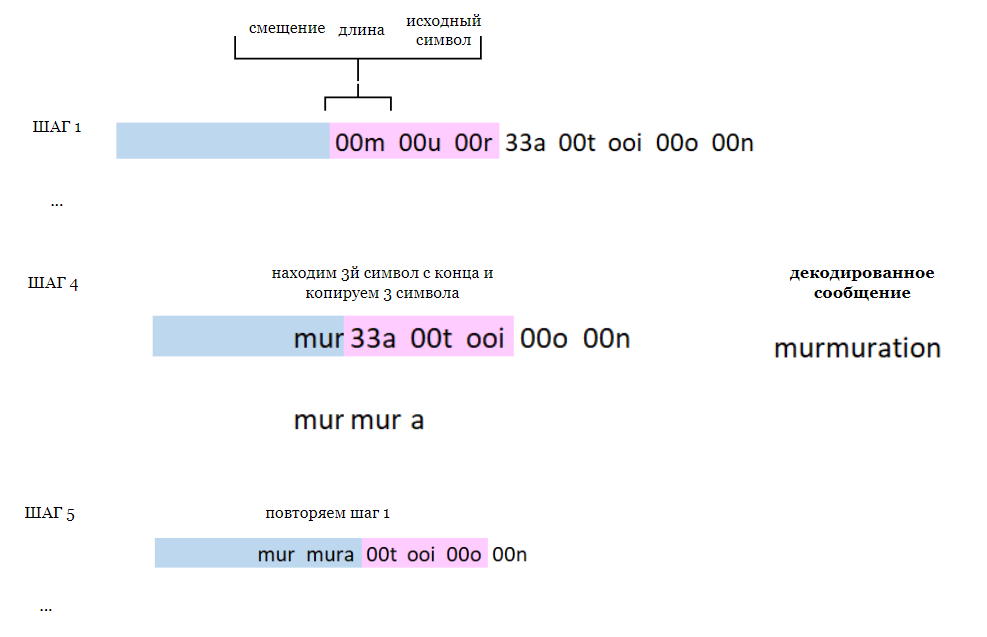
Пространственная сложность:

В данном методе требуется память для хранения словаря. Сам алгоритм использует только текцщие данные и ссылки на предыдущие данные, что делает его линейным.

, где n – длина исходных данных.

Временная сложность:

Сложность складывается из поиска по окну для каждого символа последовательности. В случае достижения длины окна близкой к длине последовательности, сложность становится квадратичной. При использовании суффиксального массива может дойти до O(n).

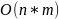, где n — длина исходных данных

m — максимальная длина окна (или буфера) для поиска совпадений

 LZ78 - Lempel-Ziv 1978

Метод сжатия без потерь, использующий технику поиска повторяющихся последовательностей данных.

Работа алгоритма:

Шаг 1: Создание пустого словаря для хранения ранее встреченных последовательностей.

Шаг 2: Поиск максимального совпадения для каждого встреченного с начала последовательности символа. При этом к пустой строке прибавляется текущий символ до первого совпадения или конца сообщения.

Шаг 3: Новая последовательность записывается в словарь и его индекс увеличивается до следующего добавления.

Шаг 4: Указатель также сдвигается до следующего символа.

Шаги 2 – 3 повторяются с указанного места до конца последовательности.

Пример:

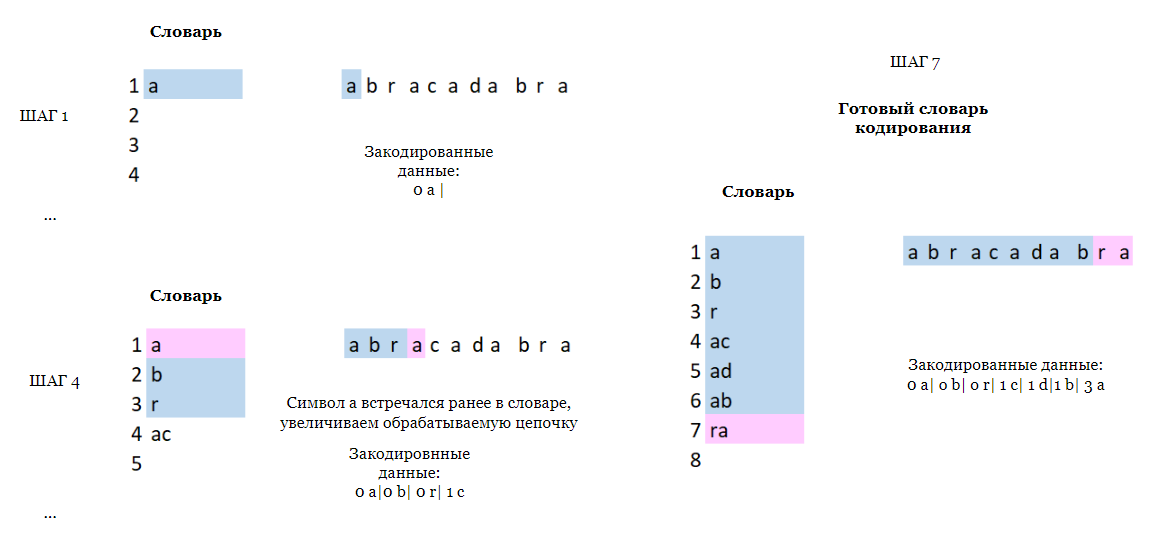
Декодирование:

В роли единицы входных данных метка с номером. Символы помещаются последовательно в словарь, если по этой метке нет соответствий в словаре. Параллельно происходит запись в исходный файл. Дойдя до метки с найденным соответствием дописываем к символам из словаря символ из кода. Также записываем в исходный файл.

Пространственная сложность:

Сложность остается линейной, так как память используется для хранения выходной информации из указателей на предыдущие символы и последовательности.

, где n — длина исходных данных

Временная сложность:

Так как проход по данным совершается один раз, временная сложность также линейна.

, где n — длина исходных данных