подготовка к экзамену 4 сем
.pdf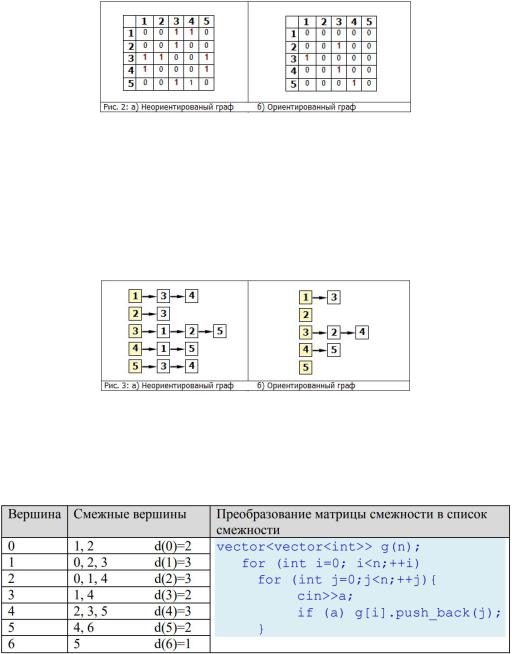
Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u]. С другой стороны этот способ очень громоздкий, так как требует O (|V|:2) памяти для хранения матрицы.
Списки смежности
Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| << |V|2).
В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).
АТЕПЕРЬ ОЧЕНЬ МНОГО ДОП ИНФЫ,
ия не знаю, надо это или нет, но, наверное, будет не лишним
Если входные данные к задаче задают матрицу смежности графа, то по ней легко получить список смежности в виде двумерного массива g, где g[i] – вектор вершин, смежных с вершиной i.
Если входные данные к задаче представляют собой список ребер, то по данному списку легко получаем и матрицу смежности, и список смежности. Ниже приведен пример для графа G входных данных в виде списка ребер: на вход программы поступают числа n – количество вершин в графе и m (1<=m<=n(n-1)/2) – количество ребер. Затем следует m пар чисел – ребра графа
Плотные графы, имеющие большое количество ребер выгоднее хранить при помощи матрицы смежности, а вот разреженные графы, имеющие небольшое количество ребер, оптимальнее хранить при помощи списка смежности.
Если граф является ориентированным, то матрица смежности в общем случае не будет являться симметричной. Для взвешенных графов, то есть графов, каждому ребру которых сопоставлено число, например, расстояние от одной вершины до другой, соответствует матрица весов. Матрица весов является обобщением матриц смежности и содержит в качестве элементов веса ребер графа.
Обход графа в глубину
Алгоритм обхода графа глубину (depth-first search)
Обход графа в глубину DFS позволяет определить вершины, достижимые из данной вершины. При обходе графа используется массив used[], хранящий информацию о том, была ли посещена вершина: used[i] = 1, если вершина уже была посещена при обходе и used[i] = 0, если вершина еще не была посещена. В начале работы алгоритма все вершины являются непосещенными:
Used[i] = 0, i = 1…n. Функция DFS получает на вход очередную вершину и вызывает себя
рекурсивно для всех еще непосещенных вершин, достижимых из данной. Из основного текста программы вызов dfs осуществляется от стартовой вершины – той, с которой мы начинаем обход
Программа обойдет вершины графа в следующем порядке: 0, 1, 4, 8, 2, 5, 3, 6, 7, 9. Оценка сложности алгоритма включает в себя следующие операции:
-просмотр всех |V| вершин, для каждой из которых v просматриваются ее соседи;
-просмотр всех соседей вершины v. При этом алгоритм проходит по ребру {v, u}. Причем, каждое такое ребро {v, u} просматривается дважды: для вершины u и для вершины v. Итоговая сложность алгоритма dfs, таким образом O(|V| + |E|).
Топологическая сортировка графа
Дан ориентированный граф, не содержащий циклов (предварительно необходимо проверить отсутствие циклов). Топологическая сортировка (topologically sort) упорядочивает вершины графа так, что все ребра идут от вершины с меньшим номером к вершине с большим номером в топологическом порядке.
Алгоритм Дейкстры для определения расстояний во взвешенном графе
Применяется для нахождения кратчайших путей от одной вершины (стартовой) до всех остальных вершин в неориентированном (или ориентированном) взвешенном графе, при условии,
что все ребра в графе имеют неотрицательные веса. Алгоритм назван в честь голландского ученого Эдсгера Дейкстры и был предложен в 1959 году.
Сложность алгоритма оценивается как O(|V|^2 + |E|)
Обход в ширину применяется для определения расстояний между вершинами в том случае, когда длина каждого ребра одинакова (невзвешенные графы). На практике более распространена
ситуация, когда каждое ребро имеет определенную длину, то есть ребра взвешены. Примером может служить карта местности с расстояниями между городами, такая, как например, на рисунке ниже. Требуется уметь определять наикратчайшее расстояние между любой парой вершин.
Рассмотрим подробнее алгоритм Дейкстры, который применяется именно для решения таких задач. Взвешенный граф удобно хранить в виде списка смежности, где для каждой вершины определен вектор пар – (смежная вершина, расстояние до этой вершины). vector<vector<pair<int,int>>>
g – список смежности графа.
ЭТО И МНОГОЕ ДРУГОЕ ПО ВТОРОЙ ССЫЛКЕ В НАЧАЛЕ БИЛЕТА
14. БЫСТРОЕ ВОЗВЕДЕНИЕ В СТЕПЕНЬ. МОДУЛЬНАЯ АРИФМЕТИКА. НАХОЖДЕНИЕ СВОБОДНОГО
ВРЕМЕНИ
ПО
ИМЕНИ
ПОУЛ
Н.
Быстрое возведение в степень (на паре был второй из двух которые я описала)
Брала отсюда: https://habr.com/ru/companies/otus/articles/779396/
Рекурсивное возведение в степень
Можно заметить, что для любого четного числа x и n выполнимо очевидное тождество
То есть всего за одну операцию умножения можно свести задачу к вдвое меньшей степени. Таким образом, показатель степени в четном представляется в виде
Если n нечетна, тогда можно перейти к степени (n-1),которая уже будет четной.
Таким образом, у нас есть реккурентная формула: от степени n мы переходим, если она четна
а иначе —
И тогда потребуется всего лишь m умножений, точнее возведений в квадрат.
Распространим это полезное наблюдение на общий случай, воспользовавшись очевидным равенством
Если показатель степени n<0, тогда
Всего будет не более 2logn переходов, прежде чем мы придем к n=0. Таким образом, мы получили алгоритм, работающий за O(log n) умножений.
Количество умножений, которое следует выполнить для возведения в степень в соответствии с описанной рекурсивной процедурой, вычисляется по формуле:
Где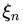 
и 
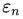— количество соответственно нулей и единиц в двоичной записи числа n. Эта величина растет крайне медленно с ростом n.
Например, если нам придется возводить число в 10000000000-ю степень, то мы обошлись бы всего 43 умножениями. Посмотрим на рекурсивный алгоритм
Бинарный алгоритм возведения в степень
Степень, в которую необходимо возвести число представляется в двоичном виде. Далее начинается проход по битам этого двоичного числа. Такой проход повторяется до тех пор, пока все биты не будут обработаны.
Количество операций возведения в квадрат одинаково и равно k, где k — длина показателя степени в n битах,
Количество же операций умножения равно количеству ненулевых элементов в двоичной записи числа n. В среднем требуется
операций умножения. Для сравнения, при стандартном способе возведения в степень требуется n-1 операций умножения, то есть количество операций может быть оценено как O(n).
В данной схеме биты показателя степени просматриваются слева направо, то есть от старшего к младшему.
Представим показатель степень n в двоичной системе
Тогда
где
Тогда число x в степени n можно записать так
И алгоритм возведения в степень при использовании данной схемы можно описать следующим образом
Представить показатель степени n в двоичном коде.
Зафиксировать индекс i и изменять его от k-1 до 0.
Если m_i=1, то текущий результат возводить в квадрат и затем умножать на х.
Если m_i=0, то текущий результат просто возводить в квадрат.
Пример: 213
Псевдокод
ЧТОБЫ БЫЛО В МОДУЛЬНОЙ АРИФМЕТИКИ ПРОСТО ВСЕ ОПЕРАЦИИ ПО ПУНКТАМ ВЫПОЛНЯЕМ ПО MOD N
Модульная арифметика (хз что тут надо написать вообще)
Для RSA (мелко ибо не так важно, Чисто для понимания почитать)
Нахождение обратного числа по по модулю N.
СВЯЗЬ ВСЕХ ТРЕХ ПУНКТОВ |
|
|
|
Быстрое возведение в степень позволяет эффективно вычислять |
, используя бинарный |
||
алгоритм. Это необходимо при работе с большими степенями в |
криптографии. |
|
|
|
( ) |
|
|
Модульная арифметика — это система вычислений с остатками, где сохраняются операции сложения, умножения и возведения в степень.
Обратный по модулю элемент x для числа a существует, если gcd(a,m)=1, и находится через расширенный алгоритм Евклида.
ПРО АЛГОРИТМ ЕВКЛИДА И НАХОЖДЕНИЕ ОБРАТНОГО ЭЛЕМЕНТА.
Брала отсюда https://yandex.ru/video/preview/14851726330611413119
15.
АЛГОРИТМ
ГЕНЕРАЦИЯ
КЛЮЧЕЙ
ДЛЯ
RSA.
ПРО ФУНКЦИЮ ЭЙЛЕРА
Текст до скринов - это степик с того сема, в целом неплохо описано (в конец кратко тоже есть)
RSA — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел. Безопасность этого алгоритма основана на сложности разложения на множители произведения двух простых чисел.
Система шифрования RSA.
Предположим, Алиса хочет послать Бобу сообщение m. Это можно сделать с помощью системы шифрования RSA.
Асимметричные криптографические системы основаны на так называемых односторонних функциях с секретом. Под односторонней понимается такая функция y=f(x), которая легко вычисляется при имеющемся x, но аргумент x при заданном значении функции вычислить сложно. Аналогично, односторонней функцией с секретом называется функция y=f(x,k), которая легко вычисляется при заданном x, причём при заданном секрете k аргумент x по заданному y восстановить просто, а при неизвестном k – сложно.
Подобным свойством обладает операция возведения числа в степень по модулю:
Первое выражение. Здесь число c получено в результате возведения в степень числа m по модулю n. Назовём это действие шифрованием.
Тогда становится очевидно, что m выступает в роли открытого текста, а c – шифротекста. Результат c зависит от степени e, в которую мы возводим m, и от модуля n, по которому мы получаем результат шифрования.
Эту пару чисел (e,n) мы будем называть открытым ключом. Им будем шифровать сообщение.
Смотрим на второе действие. Здесь d является параметром, с помощью которого мы получаем исходный текст m из шифротекста c. (d,n) мы назовём закрытым ключом и выдадим его Бобу, чтобы он смог расшифровать сообщение Алисы.
Ключи Боба.
Давайте выберем число n такое, что: n=pq
где p и q – некоторые разные простые числа. Для такого n функция Эйлера имеет вид: φ(n)=(p−1)(q−1)
Такой выбор n обусловлен следующим. Как вы могли заметить ранее, закрытый ключ d можно получить, зная открытый e. Зная числа p и q, вычислить функцию Эйлера не является сложной задачей, равно как и нахождение обратного элемента по модулю. Однако в открытом ключе указано именно число n. Таким образом, чтобы вычислить значение функции Эйлера от n (а затем получить закрытый ключ), необходимо решить задачу факторизации, которая является вычислительно сложной задачей для больших n (в современных системах, основанных на RSA, n имеет длину 2048 бит).
Возвращаемся к генерации ключей. Выберем целое число e, чтобы выполнялись условия:
Для него вычислим число d: