
подготовка к экзамену 4 сем
.pdf
Return s_new
# обратное преобразование
Def imtf(s):
T = [chr(i) for i in range(128)] S_new = ""
For s in s:
I = ord(s) S_new += t[i]
T = [t[i]] + t[:I] + t[i+1:] Return s_new
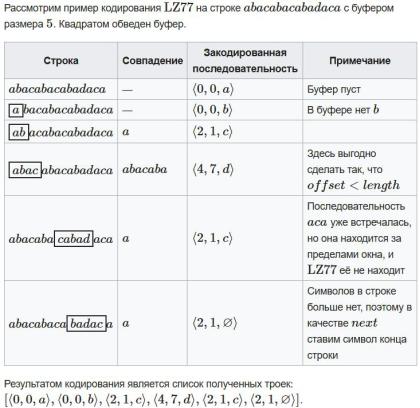
10. НЕРАВЕНСТВО КРАФТА-МАКМИЛЛАНА. НЕРАВЕНСТВО ЙЕНСЕНА. ДОКАЗАТЕЛЬСТВО ОГРАНИЧЕНИЯ СНИЗУ СРЕДНЕЙ ДЛИНЫ РАЗДЕЛИМЫХ КОДОВ ЭНТРОПИЕЙ.



11. Lz77,
Lz77, lz78
lz78
Lz77
Алгоритм:
Пока не дошли до конца строки:
Ищем индекс j наибольшего вхождения s[i:I+m] в буфере buff = s[i-n:I] Записываем триплет (n-j-1,m,s[i+m])
Сдвигаемся на m+1 символ вперед.
Код стивена:
Def lz77(s): Buffer_size = 10 String_size = 10 Coding_list = [] Buffer = ""
N = len(s) I = 0
While i < n:
Buffer = s[max(0,i-buffer_size) : I] Print(i, repr(buffer)) New_buffer_size = len(buffer) Shift = -1
For j in range(string_size, -1, -1): Subs = s[i : Min(i + j,n)]
Shift = buffer.find(subs) If shift != -1:
Break
Coding_list.append((new_buffer_size - shift, len(subs), s[i + len(subs)]))
I += len(subs)+1
Return coding_list
# декодирование lz77
Def ilz77(compressed_message):
Compressed_message = [(0,0,"A"), (0,0,"B"),(2,2,"C"),(5,4,"E")] S = ""
For t in compressed_message: Shift, length, symbol = t Print(t)
N =len(s)
S += s[n-shift : N-shift+length]+ symbol Return s
Пример стивена
N = 4
Abcdabababc = (0,0,”A”) (0,0,”B”) (0,0,”C”) (0,0,”D”) (4,2,”A”) (0,0,”B”) (2,2,”B”)
Пример из викиконспектов
Преимущества: Понижение энтропии сообщения -> более эффективное сжатие энтропийным
кодировщиком. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Недостатки: Необходимость поиска в буфере наибольшей подстроки |
|
|
|
|
|
|
|
||||||||||||
Оценка временной сложности: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для каждого символа выполняется поиск совпадений в окне, что занимает |
|
(w - размер |
|||||||||||||||||
Оценка |
|
|
|
( ) |
|
|
|
|
|
|
|
сложность |
|
. |
|||||
окна, l |
- |
|
размер буфера). |
Всего |
символов n, значит общая |
временная |
|
( ) |
данным. |
|
|||||||||
Декодирование выполняется за |
|
, так как происходит однократный проход по сжатым |
|
() |
|
||||||||||||||
данных. |
|
|
|
пространственной сложности: |
|
|
() |
|
|
|
|
|
|
|
|||||
|
|
|
( ) |
|
|
|
|
|
|
|
для входных данных |
||||||||
Алгоритм хранит скользящее окно размером |
|
и буфер размером |
|
||||||||||||||||
размером |
|
, что требует |
|
|
|
|
занимает |
|
|
для хранения декодированных |
|||||||||
|
|
памяти. Декодирование |
|
|
|
|
|
|
|
|
|
|
|||||||
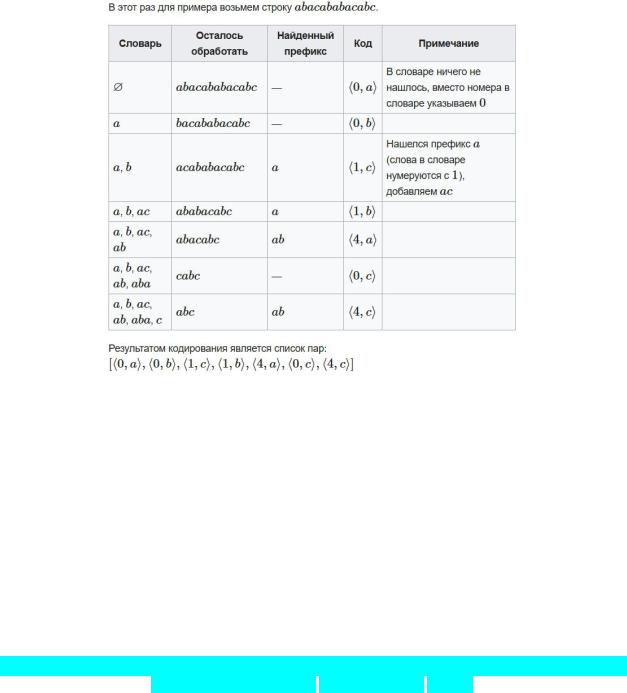
Lz78
Вместо словаря, находящегося в скользящем окне, используем отдельный словарь, добавляя в него новые коды по мере необходимости.
Алгоритм:
Пока не дошли до конца строки:
Ищем наибольшего вхождения s[i:I+m] в словаре
Записываем код наибольшего вхождения s[i:I+m] и следующий символ (dict(s[i:I+m]), s[i+m]) в выходную строку
Добавляем в словарь последовательность s[i:I+m+1] и присваиваем ей код
Пример из викиконспектов
Преимущества: В отличие от lz77 не требуется выбирать подходящий размер буфера.
Недостатки: Неограниченный рост словаря. Несмотря на то, что словарь не передается и строится декодером во время работы, это приводит к увеличению длины кодов последовательностей.
|
|
Оценка временной сложности: |
|
|
|
|
|
( ) |
|
|
|
|
|||||||
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Для каждого символа входных данных алгоритм проверяет, существует ли текущая подстрока |
|||||||||||||||||
в словаре - |
|
|
, в худшем случае может |
достигнуть |
2 |
, если |
все символы |
уникальны. |
|||||||||||
|
|
Оценка |
|
|
() |
|
|
( ), г |
де m - число записей в выходной массив. |
||||||||||
Формирование закодированных данных требует |
|||||||||||||||||||
Декодирование так же займет |
|
|
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
пространственной сложности: |
|
|
|
|
|
|
|
|
|
|||||
( ) |
|
Для |
словаря, хранящего |
уникальные |
последовательности, потребуется |
|
, где k - |
||||||||||||
|
( ) |
|
( ) |
|
|
|
|
( ) |
|
|
|
|
|
Выходные данные займут |
|||||
количество последовательностей (если данные несжимаемы, оно равно n). |
|
( ) |
|
||||||||||||||||
|
. |
Итого |
|
|
или для худшего слушая |
|
2 |
, |
если данные не были сжаты. Декодирование |
||||||||||
займет |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. СУФФИКСНЫЙ МАССИВ. СВЯЗЬ СУФФИКСНОГО МАССИВА И МАТРИЦЫ БАРРОЗА-УИЛЛЕРА, АЛЬГОРИТМ
АЛЬГОРИТМ SA-IS.
SA-IS.
(Вики + преза Стивена)
Суффиксный массив
Про префиксы и суффиксы в целом:

Cуффиксным массивом строки s[1..n] называется массив suf целых чисел от 1 до n, такой, что суффикс s[suf[i]..n] — i-й в лексикографическом порядке среди всех непустых суффиксов строки s.
Согласно определению суффиксного массива, для его построения достаточно отсортировать все суффиксы строки. Заменим сортировку суффиксов строки α на сортировку циклических сдвигов строки α$, где символ $ строго меньше любого символа из α. Тогда если в упорядоченных циклических сдвигах отбросить суффикс, начинающийся на $, то получатся упорядоченные суффиксы исходной строки α.
Суффиксное дерево:
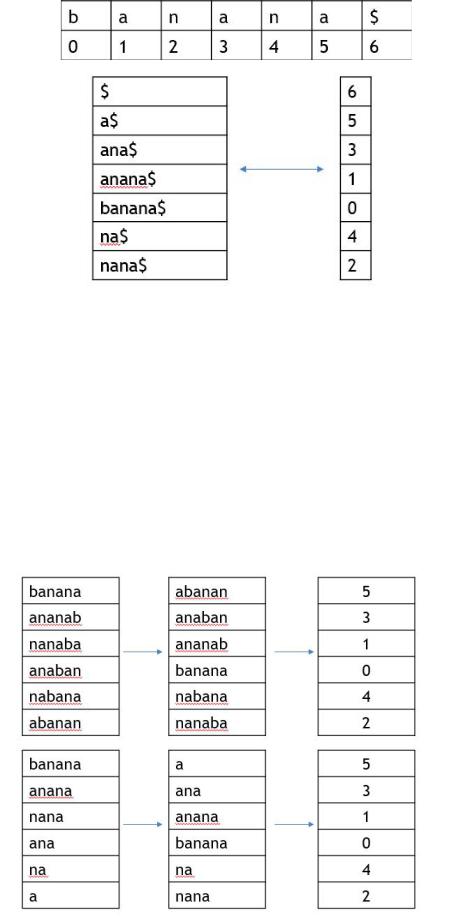
Отметим: лексикографически пустой символ (у нас это $) стоит выше остальных. Суффиксный массив (как и матрицу BWT) можно компактно представить с помощью
индексов символов, с которых начинается суффикс.
Восстановление суффиксного массива: Suf[i] = S[sufArr[i]:]
Не путаем перестановку, порождаемую BWT, и краткой записью самого массива. В первом случае для восстановления массива нужна S’ = BWT(S), во втором исходная строка.
Связь матрицы BWT и суффиксного массива
На картинке в первом случае получили сначала матрицу циклических сдвигов, затем отсортировали ее и представили в краткой форме (цифра означает индекс в исходном слове символа, с которого начинается данный сдвиг).
Во втором случае выписали матрицу суффиксов, затем отсортировали эти суффиксы и получили краткую форму этой матрицы (цифра означает индекс символа в исходном слове, с которого начинается суффикс).
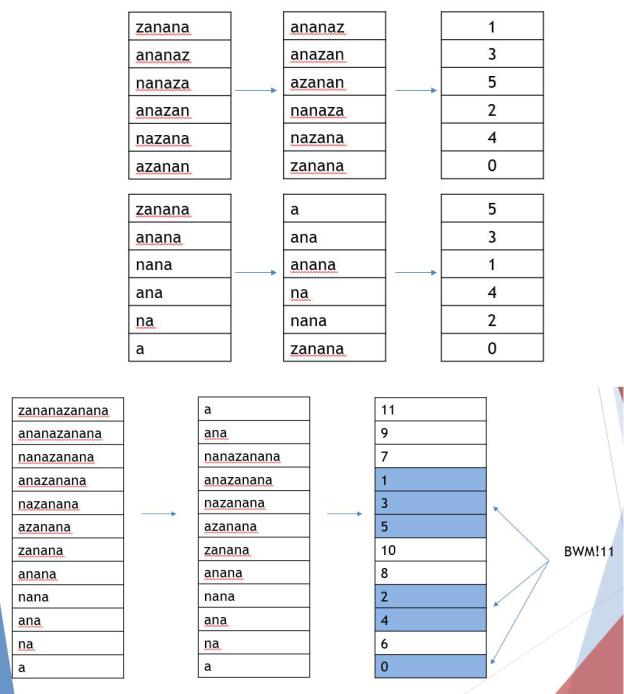
Тем не менее, если мы возьмем другую строку, s = zanana, то получившиеся матрицы в кратком виде не совпадут:
Взяв строку s = zananazanana получим:
Алгоритм SA-IS
Во-первых вот пдф, где вроде много про этот алгоритм, но на английском (потому что на русском в интернете практически ничего нет про это): https://www.cs.helsinki.fi/u/tpkarkka/opetus/11s/spa/lecture11.pdf
И как я поняла, алгоритм используется как для построения суффиксного массива, так и для BWT, хотя выше было про то что BWT можно построить с помощью суффиксного массива.
Вот еще чуть-чуть инфы из интернета:
Алгоритм SA-IS (Suffix Array Induced Sorting) — метод построения массива суффиксов (SA)
заданной строки. Описание алгоритма
Алгоритм основан на рекурсивной декомпозиции и индуцированной сортировке. Он выполняет следующие шаги:
1 Классифицирует позиции в строке как S-тип или L-тип в зависимости от того, лексикографически меньше или больше суффикс, начинающийся с этой позиции, чем суффикс в соседней правой позиции.
2 Разбивает входную строку на подстроки LMS, которые начинаются с позиции типа LMS и продолжаются до следующей соседней позиции типа LMS.
3 Лексикографически сортирует подстроки LMS с помощью индуцированной сортировки.
4 Заменяет во входной строке подстроки LMS соответствующими им отсортированными рангами, формируя новую, уплотнённую строку.
5 Выполняет рекурсивную декомпозицию: алгоритм повторно применяется для построения массива суффиксов для сжатой строки.
6 Создаёт массив суффиксов для входной строки из массива суффиксов сжатой строки с помощью другого раунда индуцированной сортировки.
13. ГРАФ,
ГРАФ, ОРИЕНТИРОВАННЫЙ
ОРИЕНТИРОВАННЫЙ ГРАФ.
ГРАФ. СПОСОБЫ
СПОСОБЫ ХРАНЕНИЯ
ХРАНЕНИЯ ГРАФА.
ГРАФА.
Ист: https://habr.com/ru/articles/65367/ https://modern-develop.ru/sites/default/files/attachment/zanyatie7_grafy.pdf
Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Графом G называется совокупность множеств G = (V(G), E(G)), где V(G) — непустое конечное множество элементов, называемых вершинами графа, а E(G) — множество пар элементов
из V(G) (необязательно различных), называемых ребрами графа. E
Вориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи).
Внеориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то
значит что существует связь (b, a).
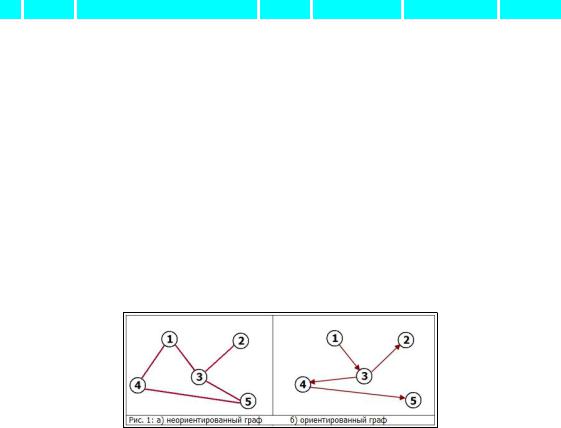
Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис
1.б, [(1), (3), (4), (5)].
Способы хранения (представления) графов
Матрица смежности
Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V|2).
В данном представлении мы заполняем матрицу размером |V| x |V| следущим образом: A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
