
подготовка к экзамену 4 сем
.pdf
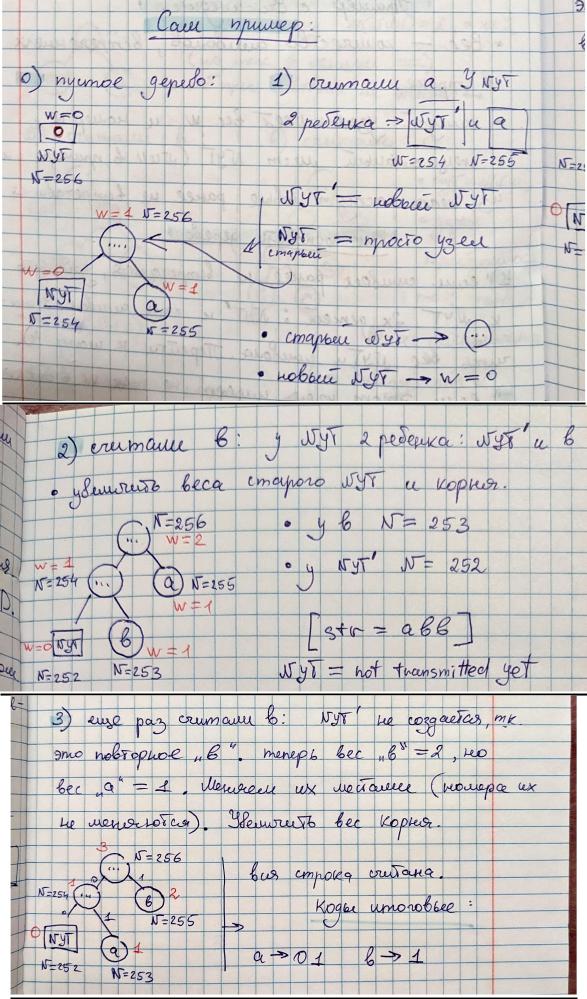

Канонические коды Хаффмана

ВЕСЬ КОД С ХАФФМАНОМ ОТ СТИВЕНА
#Класс узла для дерева Хаффмана class Node():
def __init__(self, symbol = None, counter = None, left = None, right =None, parent = None): self.symbol = symbol
self.counter = counter self.left = left self.right = right self.parent = parent
def __lt__(self, other):
return self.counter < other.counter
#Статический алгоритм Хаффмана
def HA(S):
C = count_symb(S) list_of_leafs = []
Q = queue.PriorityQueue() for i in range(128):
if C[i] != 0:
leaf = Node(symbol=chr(i), counter=C[i]) list_of_leafs.append(leaf)
Q.put(leaf) while Q.qsize() >= 2:
left_node = Q.get() right_node = Q.get()
parent_node = Node(left=left_node,right=right_node) left_node.parent = parent_node
right_node.parent = parent_node
parent_node.counter = left_node.counter + right_node.counter Q.put(parent_node)
codes = {}
for leaf in list_of_leafs: node = leaf
code = ""
while node.parent != None: if node.parent.left == node:
code = "0" + code else:
code = "1" + code node = node.parent
codes[leaf.symbol] = code coded_message = ""
for s in S:
coded_message += codes[s] k = 8 - len(coded_message)%8
coded_message += (8 - len(coded_message)%8)*"0" bytes_string = b""
for i in range(0,len(coded_message),8): s = coded_message[i:i+8]
x = string_binary_to_int(s) print(x)
bytes_string += x.to_bytes(1,"big") return bytes_string
#Преобразование строки размером 8 из нулей и единиц в двоичное число def string_binary_to_int(s):
X = 0
for i in range(8): if s[i] == "1":
X = X + 2**(7-i) return X
#Средняя длина кода символа в строке при заданной кодировке
def mean_length_of_codes(codes,S): P = prob_estimate(S)
L = 0
for s in S:
L += len(codes[s]) L = L/len(S)
return L
#Получение длин кодов Хаффмана def codes_to_length(codes):
symbol_lengths = {}
for item in codes.items(): symbol = item[0]
symbol_lengths[symbol] = len(item[1]) return symbol_lengths
#Преобразование длин кодов Хаффмана в канонические коды def length_to_codes(symbol_lengths):
symbol_lengths = dict(sorted(symbol_lengths.items(), key = lambda item: item[1]))
# print(symbol_lengths) codes = {}

i = 0
for item in symbol_lengths.items(): symbol = item[0]
L = item[1] if i == 0:
code = 0 else:
code = (prev_code + 1) * 2**(L-prev_L) new_s = f'0b{code:032b}'
codes[symbol] = new_s[-L:] prev_code = code
prev_L = L i += 1
return codes
8. АРИФМЕТИЧЕСКОЕ КОДИРОВАНИЕ. АРИФМЕТИЧЕСКОЕ КОДИРОВАНИЕ НА ДЛИННОМ ЦЕЛОМ.
ЦЕЛОМ.
Арифметическое кодирование (англ. Arithmetic coding) — алгоритм сжатия информации без потерь, который при кодировании ставит в соответствие тексту вещественное число из отрезка [0;1). Данный метод является энтропийным, то есть длина кода конкретного символа зависит от частоты встречаемости этого символа в тексте. Арифметическое кодирование показывает более высокие результаты сжатия, чем алгоритм Хаффмана, для данных с неравномерными распределениями вероятностей кодируемых символов.
Принцип кодирования:
Как и во всех энтропийных алгоритмах мы обладаем информацией о частоте использования каждого символа алфавита. Эта информация является исходной для рассматриваемого метода. Теперь введём понятие рабочего отрезка. Рабочим называется полуинтервал [a;b) с расположенными на нём точками. Причём точки расположены т.о., что длины образованных ими отрезков равны частоте использования символов. При инициализации алгоритма a=0 b=1.
Один шаг кодирования заключается в простой операции: берётся кодируемый символ, для него ищется соответствующий участок на рабочем отрезке. Найденный участок становится новым рабочим отрезком (т.е. его тоже необходимо разбить с помощью точек).
Эта операция выполняется для некоторого количества символов исходного потока.
Результатом кодирования цепочки символов является любое число (а также длина его битовой записи) с итогового рабочего отрезка (чаще всего берётся левая граница отрезка).
Разбор работы на примере: (Хабр)
Закодируем сообщение «ЭТОТ_МЕТОД_ЛУЧШЕ_ХАФФМАНА». Составляем таблицу частот:

Дальше составляем отрезок. В нем часть, относящаяся к определенному символу, должна иметь длину, соответствующую его частоте. Отрезок [0;1).
Берём первый символ из нашей строки, это символ «Э». Соответствующий ему отрезок – отрезок [0,96;1). Если бы мы хотели закодировать один символ, то результатом кодирования было бы любое число из этого отрезка. Но мы не остановимся на одном символе, а добавим ещё один.
Следующий символ «Т». Для этого составим новый рабочий отрезок с a=0,96 и b=1. Разбиваем этот отрезок точками точно так же, как мы сделали это для исходного отрезка и считываем новый символ «Т».
Символу «Т» соответствует диапазон [0,24;0,36), но наш рабочий отрезок уже сократился до отрезка [0,96;1). Т.е. границы нам необходимо пересчитать. Сделать это можно с помощью двух следующих формул: High=Lowold+(Highold-Lowold)*RangeHigh(x), Low=Lowold+(Highold- Lowold)*RangeLow(x), где Lowold – нижняя граница интервала, Highold – верхняя граница интервала RangeHigh и RangeLow – верхняя и нижняя границы кодируемого символа.
Пересчитываем диапазон «Т»: High = 0,96 + (1 – 0,96)*0,36 = 0,9744 Low = 0,96 + (1 – 0,96)*0,24 = 0,9696
Закодируем с помощью этих формул первое слово сообщения целиком:
Результатом кодирования будет любое число из полуинтервала [0,97218816; 0,97223424). Предположим, что результатом кодирования была выбрана левая граница полуинтервала, т.е.
число 0,97218816.
Рассмотрим процесс декодирования. Код лежит в полуинтервале [0,96;1). Т.е. первый символ сообщения «Э». Чтобы декодировать второй символ (который кодировался в полуинтервале [0,96;1)) полуинтервал нужно нормализовать, т.е. привести к виду [0;1).

Это делается с помощью следующей формулы: code=(code-RangeLow(x))/(RangeHigh(x)-RangeLow(x)),
где code – текущее значение кода. Применяя эту формулу, получаем новое значение code=(0,97218816-0,96)/(1-0,96)= 0,304704. Т.е. второй символ последовательности «Т». Снова применим формулу: code=(0,304704-0,24)/(0,36-0,24)= 0,5392. Третий символ последовательности – «О». Продолжая декодирование, по описанной схеме мы можем полностью восстановить исходный текст.
Т.о. мы с вами рассмотрели алгоритм кодирования и декодирования с помощью самого эффективного из всех энтропийных алгоритмов.
Арифметическое кодирование на длинных целых числах – это метод сжатия данных,
основанный на представлении информации в виде вещественного числа из интервала. При этом, чем точнее (больше знаков после запятой) это число, тем больше данных закодировано. Использование длинных целых чисел позволяет увеличить точность представления и, следовательно, сжимать данные более эффективно, особенно для последовательностей символов с неравномерным распределением вероятностей.
Псевдокод кодирования:
s — текст, подаваемый на вход;
n — длина исходного текста;
m — мощность алфавита исходного текста;
letters[m] — массив символов, составляющих алфавит исходного текста;
probability[m] — массив вероятностей обнаружения символа в тексте;
Segment — структура, задающая подотрезок отрезка [0;1), соответствующего конкретному символу на основе частотного анализа. Имеет поля:
left — левая граница подотрезка;
right — правая граница подотрезка;
left, right — границы отрезка, содержащего возможный результат арифметического кодирования.
struct Segment:
double left
double right
Segment[m] defineSegments(letters: char[m], probability: double[m]): Segment[m] segment
double l = 0
for i = 0 to m - 1 segment[letters[i]].left = l
segment[letters[i]].right = l + probability[i] l = segment[letters[i]].right
return segment
double arithmeticCoding(letters: char[m], probability: double[m], s: char[n]): Segment[m] segment = defineSegments(letters, probability)
double left = 0 double right = 1 for i = 0 to n - 1
char symb = s[i]
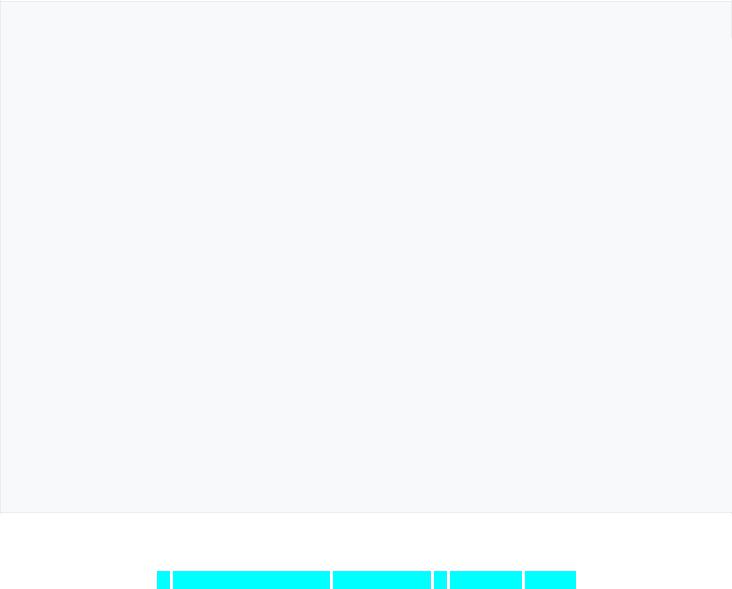
double newRight = left + (right - left) * segment[symb].right double newLeft = left + (right - left) * segment[symb].left left = newLeft
right = newRight return (left + right) / 2
Псевдокод декодирования:
code — вещественное число, подаваемое на вход;
n — длина восстанавливаемого текста;
m — мощность алфавита исходного текста;
letters[m] — массив символов, составляющих алфавит исходного текста;
probability[m] — массив вероятностей обнаружения символа в тексте;
segment — структура, задающая подотрезок отрезка [0;1), соответствующего конкретному символу на основе частотного анализа. Имеет поля:
left — левая граница подотрезка;
right — правая граница подотрезка;
character — значение символа.
struct Segment:
double left
double right
char character
Segment[m] defineSegments(letters: char[n], probability: double[n]):
Segment[m] segment
double l = 0
for i = 0 to m - 1
segment[i].left = l
segment[i].right = l + probability[i]
segment[i].character = letters[i]
l = segment[i].right
return segment
string arithmeticDecoding(letters: char[m], probability: double[m], code: double, n: int):
Segment[m] segment = defineSegments(letters, probability)
string s = ""
for i = 0 to n - 1
for j = 0 to m - 1
if code segment[j].left and code < segment[j].right
s += segment[j].character
code = (code – segment[j].left) / (segment[j].right – segment[j].left)
break
return s
9. ПРЕОБРАЗОВАНИЕ
ПРЕОБРАЗОВАНИЕ ДВИЖЕНИЯ
ДВИЖЕНИЯ К
К НАЧАЛУ
НАЧАЛУ (MTF).
(MTF).
Кодирование:
1.Для имеющийся строки инициализируем алфавит, содержащий байты от 0 до 255. В выходной массив добавляем индекс первого символа исходного слова. Например, для слова ‘robot’ первый символ строки является элементом алфавита с индексом 114, значит выходные данные имеют вид
[114].
2.Помещаем только что использованный элемент в первое место в алфавите, получаем алфавит [114,0,…255] и повторяем процесс со вторым символом. Для символа o-111 индекс в алфавите будет 112, помещаем его в выходные данные [114,112], а в алфавите индекс 111 перемещаем на первое место [111,114,0,..255]. И так далее. Получаем выходные данные [114,112,100,1,116].
Декодирование:
1. Ищем в алфавите от [0...255] элемент с индексом, равным первому элементу в закодированных данных, 114. Получаем на выходе [114], и этот символ помещается в начало алфавита [114,0,…255]. Символ с номером 112 в алфавите [114...255] - это 111, поэтому на выводе получаем [114,111] и номер 112 перемещается в начало алфавита -> [112,114,0,…255]. И так далее. Получаем строку
[114,111,98,111,116], что соответствует слову robot’.
Оценка временной сложности:
Для каждого символа входных данных нужно найти символ в списке фиксированной длинны
(256) и переместить его в начало списка. Общая сложность для обработки всех символов |
|
, где n |
||||||||||||||
- длина входных данных, |
тогда общая временная сложность |
|
. Декодирование |
займет |
|
, |
||||||||||
|
|
|
( ) |
|
|
|||||||||||
поскольку для каждого индекса в закодированных данных |
длиной n выполняется фиксированное |
|||||||||||||||
|
( ) |
|
|
|
|
|
|
( ) |
|
|||||||
количество итераций удаления и вставки элемента. |
|
|
|
|
|
|
( ). |
|
|
|||||||
пространственная сложность |
|
потребуется. |
(1) |
|
|
|
|
|
|
|
|
|
||||
Оценка пространственн й сложности: |
|
|
|
|
( ) |
|
|
|
|
|
|
|||||
Код из лабы |
|
( ) |
|
|
|
|
|
|
|
|
|
|
Итого |
|||
Для хранения алфавита |
|
|
|
, для хранения закодированных данных |
|
|
||||||||||
|
|
|
|
Для декодирования она так же составит |
|
. |
|
|
|
|
|
|||||
Def mtf_encode(data: Bytes) -> bytes:
Alphabet = bytearray(range(256))
Encoded = bytearray()
For byte in data:
Index = alphabet.index(byte)
Encoded.append(index)
Del alphabet[index]
Alphabet.insert(0, byte)
Return bytes(encoded)
Def mtf_decode(encoded_data: Bytes) -> bytes:
Alphabet = bytearray(range(256))
Decoded = bytearray()
For index in encoded_data:
Byte = alphabet[index]
Decoded.append(byte)
Del alphabet[index]
Alphabet.insert(0, byte)
Return bytes(decoded)
Код стивена
Def mtf(s):
T = [chr(i) for i in range(128)] L = []
S_new = "" For s in s:
I = t.index(s) L.append(i) S_new += chr(i)
T = [t[i]] + t[:I] + t[i+1:]
