
Верхняя оценка высоты красно-черного дерева
Если черная высота узла bh(x) — количество черных узлов на пути от узла x до его листьев, то для любого узла x в красно-черном дереве, черная высота всех путей от x до его листьев будет одинаковой.
Поскольку красные узлы могут находиться только между черными узлами, максимальная высота h дерева может быть в два раза больше черной высоты bh:
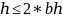
Если n — количество узлов в дереве, то максимальная черная высота bh может быть не более (черные узлы должны быть равномерно распределены).
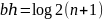
Тогда максимальная высота красно-черного дерева может быть оценена как:
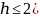 )
)
Обходы деревьев
Рассмотрим 4 обхода, примененные далее в практической части работы.
Прямой обход (preorder): сначала происходит посещение узла, затем его левого и правого поддерева.
Симметричный обход (inorder): левое поддерево, затем узел, правое поддерево.
Обратный обход (postorder): левое поддерево, правое поддерево, затем узел.
Обход в ширину: при данном обходе рассматриваются все ключи на каждом уровне слева направо, начиная с корня и двигаясь вниз.
Практическая часть
Реализовать обходы в глубину и обход в ширину для BST дерева.
П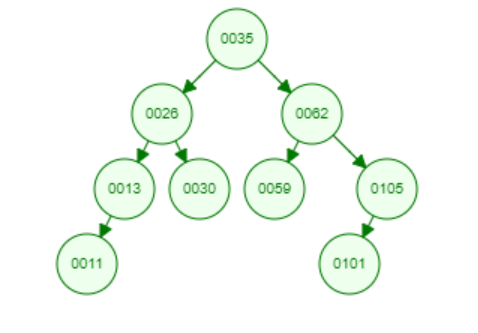 ример
дерева и работы программы для среднего
и лучшего случая:
ример
дерева и работы программы для среднего
и лучшего случая:
значения в дереве inorder:
[11, 13, 26, 30, 35, 59, 62, 101, 105]
значения в дереве preorder:
[35, 26, 13, 11, 30, 62, 59, 105, 101]
значения в дереве postorder:
[11, 13, 30, 26, 59, 101, 105, 62, 35]
значения в дереве BFT (в ширину):
[ 35,
26, 62, 13, 30, 59, 105, 11, 101]
Пример
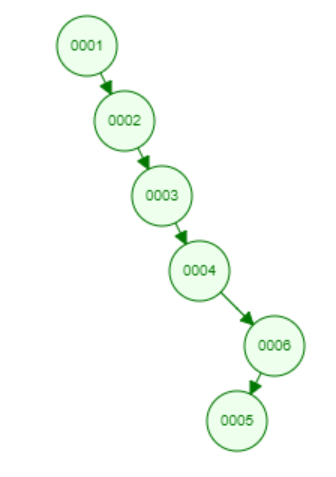
дерева и работы программы для худшего
случая:
35,
26, 62, 13, 30, 59, 105, 11, 101]
Пример
дерева и работы программы для худшего
случая:
значения в дереве inorder:
[1, 2, 3, 4, 5, 6]
значения в дереве preorder:
[1, 2, 3, 4, 6, 5]
значения в дереве postorder:
[5, 6, 4, 3, 2, 1]
значения в дереве BFT (в ширину):
[1, 2, 3, 4, 6, 5]
Какая асимпотика функции h(n) наблюдается у двоичного дерева поиска?
Лучший случай (сбалансированное дерево)
Если дерево сбалансировано, то высота дерева будет логарифмической относительно количества узлов.
h(n)=O(logn)
Средний случай (случайная вставка узлов)
При случайной вставке узлов в дерево, дерево также будет иметь высоту, близкую к логарифмической, если вставка случайна, как в нашем случае.
h(n)=O(logn)
Худший случай (вставка элементов один за другим)
В худшем случае, если элементы вставляются в строго возрастающем или убывающем порядке, каждый узел имеет только одного потомка (левого или правого). В этом случае высота дерева будет линейной.
h(n) = O(n)
Теперь реализуем зависимость высоты бинарного дерева от количества ключей, которые определены случайным образом в диапазоне от 1 до 1000. Результаты представлены на рисунке 1.
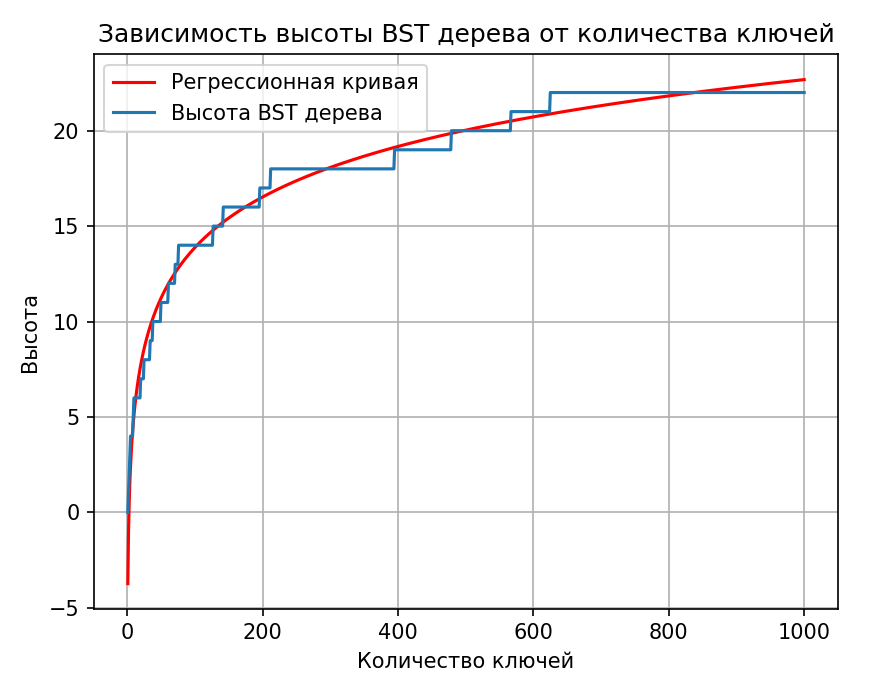
Рисунок 1 – зависимость высоты от количества ключей BST
Количество ключей |
Высота дерева |
1 |
0 |
2 |
1 |
3 |
2 |
4 |
3 |
5 - 6 |
4 |
7 - 10 |
5 |
11 |
6 |
12 |
7 |
17 - 26 |
8 |
27 - 29 |
9 |
30 - 45 |
10 |
46 - 50 |
11 |
51 - 99 |
12 |
100 - 130 |
13 |
131 - 175 |
14 |
176 - 214 |
15 |
215 - 219 |
16 |
220 - 275 |
17 |
276 - 341 |
18 |
342 - 462 |
19 |
463 - 596 |
20 |
597 - 937 |
21 |
938 - 1000 |
22 |
Таблица 1 – зависимость высоты от количества ключей в AVL дереве
По графику заметно, что в среднем случае высота BST дерева проходит по логарифмической асимптотике.
Реализовать обходы в глубину и обход в ширину для AVL дерева.
Пример дерева и работы программы:
з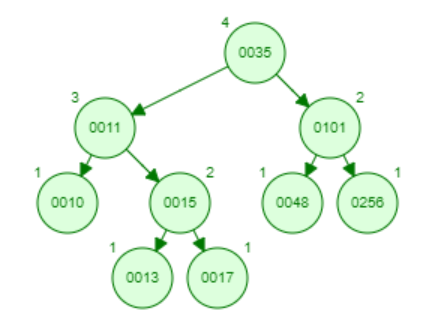 начения
в дереве inorder:
начения
в дереве inorder:
[10, 11, 13, 15, 17, 35, 48, 101, 256]
значения в дереве preorder:
[35, 11, 10, 15, 13, 17, 101, 48, 256]
значения в дереве postorder:
[10, 13, 17, 15, 11, 48, 256, 101, 35]
значения в дереве в ширину:
[35, 11, 101, 10, 15, 48, 256, 13, 17]
Теперь реализуем зависимость высоты AVL дерева от количества ключей, которые определены в диапазоне от 1 до 1000 в порядке возрастания. Результаты представлены на рисунке 2.
Теоретическая справка:
Лучший случай — h(n)=O(logn)
Средний случай — h(n)=O(logn)
Худший случай — h(n)=O(logn)
Из за балансировки высота AVL-дерева всегда ограничена логарифмом от числа узлов.
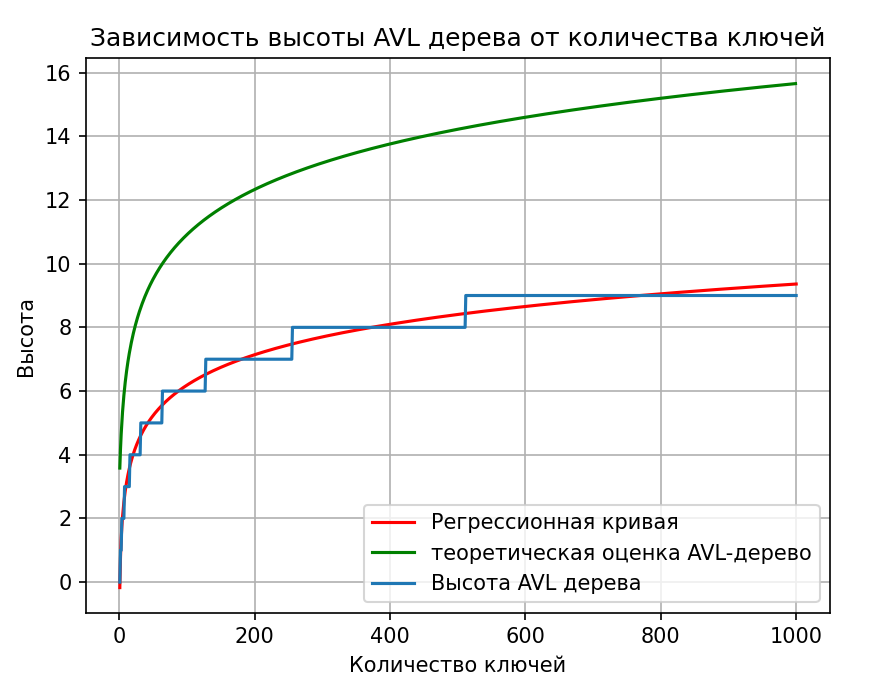
Рисунок 2 – зависимость высоты от количества ключей в AVL дереве
Количество ключей |
Высота дерева |
1 |
0 |
2 - 3 |
1 |
4 - 7 |
2 |
8 - 15 |
3 |
16 - 31 |
4 |
32 - 63 |
5 |
64 - 127 |
6 |
128 - 255 |
7 |
256 - 511 |
8 |
512 - 1000 |
9 |
Таблица 2 – зависимость высоты от количества ключей в AVL дереве
Реализовать обходы в глубину и обход в ширину для RBT дерева.
Пример дерева и работы программы:
обход inorder:
1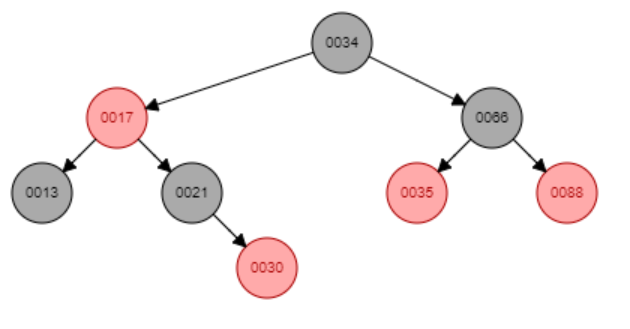 3
black 17 red 21 black 30 red 34 black 66 black 88 red
3
black 17 red 21 black 30 red 34 black 66 black 88 red
Обход: preorder
34 black 17 red 13 black 21 black 30 red 66 black 88 red
обход: postorder
13 black 30 red 21 black 17 red 88 red 66 black 34 black
обход: в ширину
34 17 66 13 21 88 30
Теперь реализуем зависимость высоты RB дерева от количества ключей, которые определены от 1 до 1000 в порядке возрастания. Результаты представлены на рисунке 3.
Теоретическая справка:
Лучший случай — h(n)=O(logn)
Средний случай — h(n)=O(logn)
Худший случай — h(n)=O(logn)
RB дерево всегда поддерживает высоту, пропорциональную logn, что происходит благодаря балансировке, которая не позволяет дереву переходить в линейную форму.
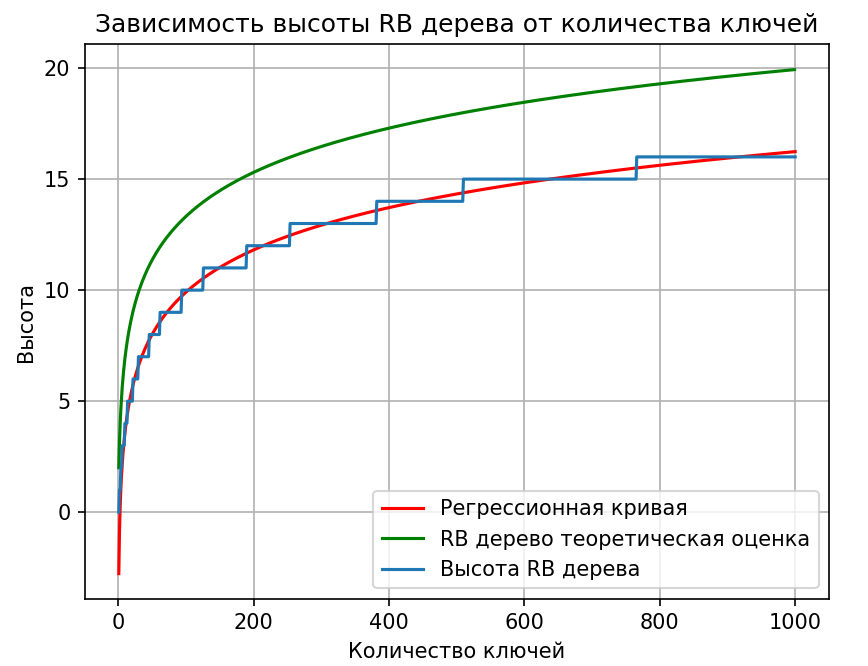
Рисунок 3 – зависимость высоты от количества ключей в Красно-Черном дереве
Количество ключей |
Высота дерева |
1 |
0 |
2 - 3 |
1 |
4 - 5 |
2 |
6 - 9 |
3 |
10 - 13 |
4 |
14 - 21 |
5 |
22 - 29 |
6 |
30 - 45 |
7 |
46 - 61 |
8 |
62 - 93 |
9 |
94 - 125 |
10 |
126 - 189 |
11 |
190 - 253 |
12 |
254 - 381 |
13 |
382 - 509 |
14 |
510 - 1000 |
15 |
Таблица 3 – зависимость высоты от количества ключей в Красно-Черном дереве
При условии монотонного возрастания ключей в AVL и RBT деревьях, наблюдается логарифмическая асимптотика.
Выводы
Сравнение с теоретической оценкой высоты:
По выведенным формулам теоретической оценки высоты, представленной на рисунке 4, можно сделать вывод о соответствии теоретических данных, практическим.
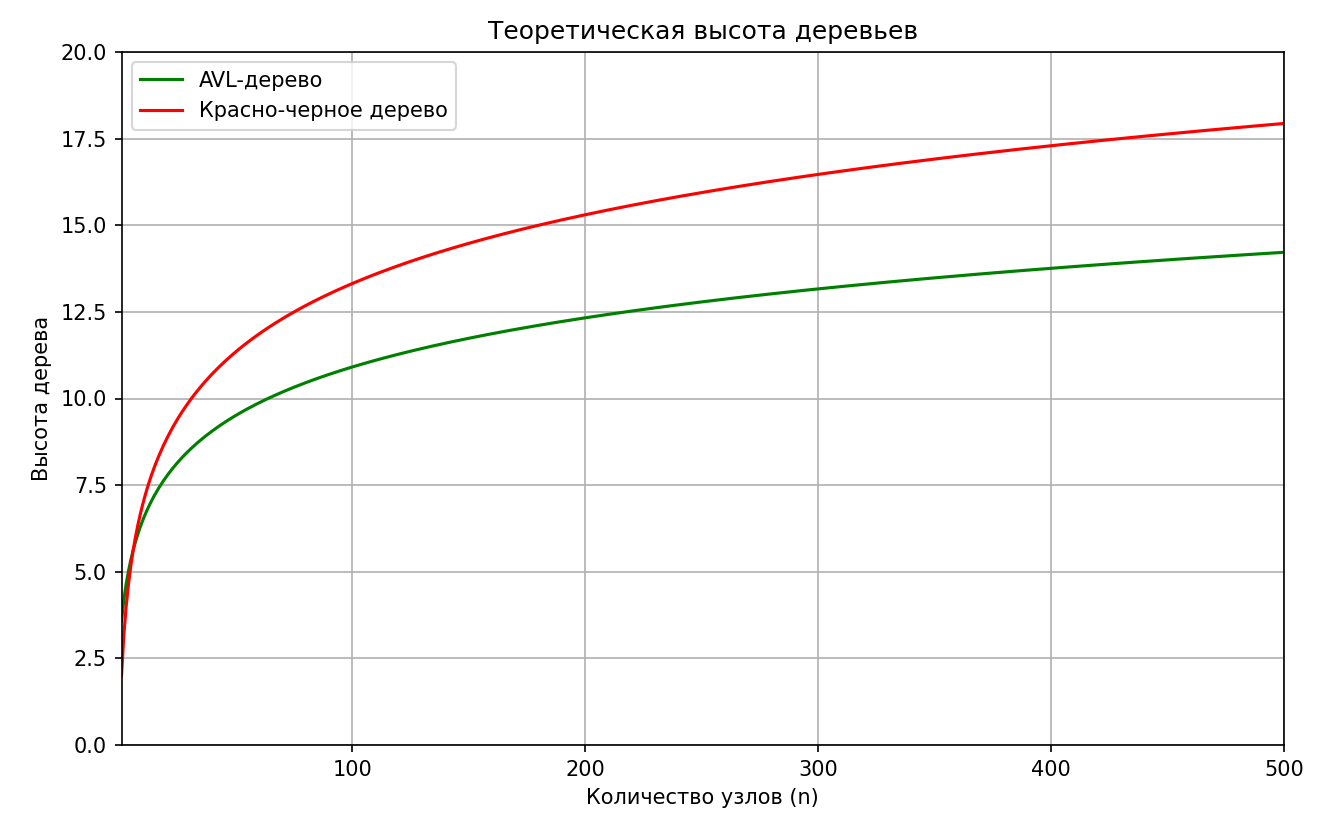
Рисунок 4. Теоретический график зависимости высоты от количества элементов
Также исходя из теоретических и практических данных можно сделать вывод о наибольшей эффективности AVL дерева среди трех представленных вариантов.
Ссылка на код:
Код программы:
BST дерево
from collections import deque
import random
import matplotlib.pyplot as plt
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, value):
if self.root is None:
self.root = TreeNode(value)
else:
self._insert_recursively(self.root, value)
def _insert_recursively(self, node, value):
if value < node.value:
if node.left is None:
node.left = TreeNode(value)
else:
self._insert_recursively(node.left, value)
elif value > node.value:
if node.right is None:
node.right = TreeNode(value)
else:
self._insert_recursively(node.right, value)
def search(self, value):
return self._search_recursively(self.root, value)
def _search_recursively(self, node, value):
if node is None or node.value == value:
return node
if value < node.value:
return self._search_recursively(node.left, value)
else:
return self._search_recursively(node.right, value)
def delete(self, value):
self.root = self._delete_recursively(self.root, value)
def _delete_recursively(self, node, value):
if not node:
return node
if value < node.value:
node.left = self._delete_recursively(node.left, value)
elif value > node.value:
node.right = self._delete_recursively(node.right, value)
else:
if not node.left:
return node.right
elif not node.right:
return node.left
min_larger_node = self._find_min(node.right)
node.value = min_larger_node.value
node.right = self._delete_recursively(node.right, min_larger_node.value)
return node
def _find_min(self, node):
current = node
while current.left is not None:
current = current.left
return current
def inorder(self):
return self._inorder_recursively(self.root)
def _inorder_recursively(self, node):
return self._inorder_recursively(node.left) + [node.value] + self._inorder_recursively(
node.right) if node else []
def preorder(self):
return self._preorder_recursively(self.root)
def _preorder_recursively(self, node):
return [node.value] + self._preorder_recursively(node.left) + self._preorder_recursively(
node.right) if node else []
def postorder(self):
return self._postorder_recursively(self.root)
def _postorder_recursively(self, node):
return self._postorder_recursively(node.left) + self._postorder_recursively(node.right) + [
node.value] if node else []
def breadth_first_traversal(self):
if not self.root:
return []
result = []
queue = deque([self.root])
while queue:
node = queue.popleft()
result.append(node.value)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result
def height_Tree(self, node):
if node is None:
return -1
else:
left_height = self.height_Tree(node.left)
right_height = self.height_Tree(node.right)
return max(left_height, right_height) + 1
AVL дерево
from collections import deque
import random
import matplotlib.pyplot as plt
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, value):
if self.root is None:
self.root = TreeNode(value)
else:
self._insert_recursively(self.root, value)
def _insert_recursively(self, node, value):
if value < node.value:
if node.left is None:
node.left = TreeNode(value)
else:
self._insert_recursively(node.left, value)
elif value > node.value:
if node.right is None:
node.right = TreeNode(value)
else:
self._insert_recursively(node.right, value)
def search(self, value):
return self._search_recursively(self.root, value)
def _search_recursively(self, node, value):
if node is None or node.value == value:
return node
if value < node.value:
return self._search_recursively(node.left, value)
else:
return self._search_recursively(node.right, value)
def delete(self, value):
self.root = self._delete_recursively(self.root, value)
def _delete_recursively(self, node, value):
if not node:
return node
if value < node.value:
node.left = self._delete_recursively(node.left, value)
elif value > node.value:
node.right = self._delete_recursively(node.right, value)
else:
if not node.left:
return node.right
elif not node.right:
return node.left
min_larger_node = self._find_min(node.right)
node.value = min_larger_node.value
node.right = self._delete_recursively(node.right, min_larger_node.value)
return node
def _find_min(self, node):
current = node
while current.left is not None:
current = current.left
return current
def inorder(self):
return self._inorder_recursively(self.root)
def _inorder_recursively(self, node):
return self._inorder_recursively(node.left) + [node.value] + self._inorder_recursively(
node.right) if node else []
def preorder(self):
return self._preorder_recursively(self.root)
def _preorder_recursively(self, node):
return [node.value] + self._preorder_recursively(node.left) + self._preorder_recursively(
node.right) if node else []
def postorder(self):
return self._postorder_recursively(self.root)
def _postorder_recursively(self, node):
return self._postorder_recursively(node.left) + self._postorder_recursively(node.right) + [
node.value] if node else []
def breadth_first_traversal(self):
if not self.root:
return []
result = []
queue = deque([self.root])
while queue:
node = queue.popleft()
result.append(node.value)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result
def height_Tree(self, node):
if node is None:
return -1
else:
left_height = self.height_Tree(node.left)
right_height = self.height_Tree(node.right)
return max(left_height, right_height) + 1
RBT дерево
import matplotlib.pyplot as plt
class Node:
def __init__(self, data, color='red'):
self.data = data
self.color = color
self.left = None
self.right = None
self.parent = None
class RedBlackTree:
def __init__(self):
self.NIL = Node(data=None, color='black')
self.root = self.NIL
def insert(self, data):
new_node = Node(data)
new_node.left = self.NIL
new_node.right = self.NIL
parent = None
current = self.root
while current != self.NIL:
parent = current
if new_node.data < current.data:
current = current.left
else:
current = current.right
new_node.parent = parent
if parent is None:
self.root = new_node
elif new_node.data < parent.data:
parent.left = new_node
else:
parent.right = new_node
new_node.color = 'red'
self.fix_insert(new_node)
def fix_insert(self, node):
while node != self.root and node.parent.color == 'red':
if node.parent == node.parent.parent.left:
uncle = node.parent.parent.right
if uncle.color == 'red':
node.parent.color = 'black'
uncle.color = 'black'
node.parent.parent.color = 'red'
node = node.parent.parent
else:
if node == node.parent.right:
node = node.parent
self.rotate_left(node)
node.parent.color = 'black'
node.parent.parent.color = 'red'
self.rotate_right(node.parent.parent)
else:
uncle = node.parent.parent.left
if uncle.color == 'red':
node.parent.color = 'black'
uncle.color = 'black'
node.parent.parent.color = 'red'
node = node.parent.parent
else:
if node == node.parent.left:
node = node.parent
self.rotate_right(node)
node.parent.color = 'black'
node.parent.parent.color = 'red'
self.rotate_left(node.parent.parent)
self.root.color = 'black'
def rotate_left(self, node):
new_parent = node.right
node.right = new_parent.left
if new_parent.left != self.NIL:
new_parent.left.parent = node
new_parent.parent = node.parent
if node.parent is None:
self.root = new_parent
elif node == node.parent.left:
node.parent.left = new_parent
else:
node.parent.right = new_parent
new_parent.left = node
node.parent = new_parent
def rotate_right(self, node):
new_parent = node.left
node.left = new_parent.right
if new_parent.right != self.NIL:
new_parent.right.parent = node
new_parent.parent = node.parent
if node.parent is None:
self.root = new_parent
elif node == node.parent.right:
node.parent.right = new_parent
else:
node.parent.left = new_parent
new_parent.right = node
node.parent = new_parent
def search(self, data):
current = self.root
while current != self.NIL:
if data == current.data:
return current
elif data < current.data:
current = current.left
else:
current = current.right
return None
def in_order_traversal(self, node):
if node != self.NIL:
self.in_order_traversal(node.left)
print(node.data, node.color)
self.in_order_traversal(node.right)
def preorder(self, node):
if node != self.NIL:
print(node.data, node.color)
self.preorder(node.left)
self.preorder(node.right)
def postorder(self, node):
if node != self.NIL:
self.postorder(node.left)
self.postorder(node.right)
print(node.data, node.color)
def print_preorder(self):
self.preorder(self.root)
def print_postorder(self):
self.postorder(self.root)
def breadth_first(self):
if self.root == self.NIL:
return
queue = [self.root]
while queue:
current = queue.pop(0)
print(current.data)
if current.left != self.NIL:
queue.append(current.left)
if current.right != self.NIL:
queue.append(current.right)
def delete(self, key):
node = self.search(key)
if node == self.NIL:
return
y = node
y_original_color = y.color
if node.left == self.NIL:
x = node.right
self.transplant(node, node.right)
elif node.right == self.NIL:
x = node.left
self.transplant(node, node.left)
else:
y = self.minimum(node.right)
y_original_color = y.color
x = y.right
if y.parent == node:
x.parent = y
else:
self.transplant(y, y.right)
y.right = node.right
y.right.parent = y
self.transplant(node, y)
y.left = node.left
y.left.parent = y
y.color = node.color
if y_original_color == "black":
self.delete_fixup(x)
def delete_fixup(self, x):
while x != self.root and x.color == "black":
if x == x.parent.left:
sibling = x.parent.right
if sibling.color == "red":
sibling.color = "black"
x.parent.color = "red"
self.rotate_left(x.parent)
sibling = x.parent.right
if sibling.left.color == "black" and sibling.right.color == "black":
sibling.color = "red"
x = x.parent
else:
if sibling.right.color == "black":
sibling.left.color = "black"
sibling.color = "red"
self.rotate_right(sibling)
sibling = x.parent.right
sibling.color = x.parent.color
x.parent.color = "black"
sibling.right.color = "black"
self.rotate_left(x.parent)
x = self.root
else:
sibling = x.parent.left
if sibling.color == "red":
sibling.color = "black"
x.parent.color = "red"
self.rotate_right(x.parent)
sibling = x.parent.left
if sibling.left.color == "black" and sibling.right.color == "black":
sibling.color = "red"
x = x.parent
else:
if sibling.left.color == "black":
sibling.right.color = "black"
sibling.color = "red"
self.rotate_left(sibling)
sibling = x.parent.left
sibling.color = x.parent.color
x.parent.color = "black"
sibling.left.color = "black"
self.rotate_right(x.parent)
x = self.root
x.color = "black"
def minimum(self, node):
while node.left != self.NIL:
node = node.left
return node
def transplant(self, u, v):
if u.parent is None:
self.root = v
elif u == u.parent.left:
u.parent.left = v
else:
u.parent.right = v
v.parent = u.parent
def height_Tree(self, node):
if node is None:
return -2
else:
left_height = self.height_Tree(node.left)
right_height = self.height_Tree(node.right)
return max(left_height, right_height) + 1
