МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

ОТЧЕТ

по Лабораторной работе №2

по дисциплине Алгоритмы и структуры данных

Тема: «Самобалансирующие двоичные деревья поиска»

Студентка группы 3352:

Преподаватель:

Санкт-Петербург

2024

Цель лабораторной работы:

Реализация самобалансирующихся деревьев поиска и экспериментальная проверка оценок высоты данных деревьев.

Теоретическая часть:

1. Определение АВЛ дерева. Кратко описать алгоритм вставки/удаления с последующей балансировкой для АВЛ-дерева. Получить верхнюю оценку высоты АВЛ-дерева.

2. Определение красно-черного дерева. Кратко описать алгоритм вставки/удаления с последующей балансировкой для красно-черного дерева.-дерева. Получить верхнюю оценку высоты красно-черного дерева.

Практическая часть:

1. Реализовать бинарное дерево поиска, красно-черное дерево и АВЛ дерево (структура, балансировка, операции вставки/удаления/поиска).

2. Получить зависимость высоты дерева поиска от количества ключей, при условии, что значение ключа - случайная величина, распределенная равномерно. Какая асимпотика функции h(n) наблюдается у двоичного дерева поиска?

3. Получить зависимость АВЛ и красно-черного дерева поиска от количества ключей, при условии, что значения ключей монотонно возрастают.

3. Вывести полученные результаты на графики.

4. Сравнить с теоретической оценкой высоты.

5. Реализовать обходы в глубину и обход в ширину двоичного дерева с выводом результата.

Теоретическая часть

АВЛ-дерево (AVL Tree)

АВЛ-дерево — структура данных, представляющая собой сбалансированное по высоте двоичное дерево поиска, для которого верно утверждение: высота двух поддеревьев различается не более чем на 1.

Основные операции AVL Tree

1. Вставка:

Для начала опишем вставку для бинарного дерева:

Сравнить значение ключа с корнем. В случае, если элемент больше – перейти в правое поддерево, меньше – в левое. Операцию повторить до нахождения места для вставки узла.

После проделанной операции требуется обновить высоты всех узлов от вставленного до корня. Высота равна максимальной высоте поддерева + 1. На этом моменте может быть нарушен баланс AVL дерева, который определяется как разность между левым и правым поддеревом. В случае, если он равен +2 или -2, дерево становится не сбалансированным.

Случай: баланс равен +2

Баланс левого поддерева равен +1 или 0 (левый левый случай) — выполняем правый поворот.

Баланс левого поддерева равен -1 (левый правый случай) —выполняем левый поворот на левом поддереве, затем правый поворот на текущем узле.

Случай: баланс равен -2

Баланс правого поддерева равен -1 или 0 (правый правый случай) —левый поворот.

Баланс его правого поддерева равен +1 (правый левый случай) —правый поворот на правом поддереве, левый поворот на текущем узле.

2. Удаление:

Опишем удаление для бинарного дерева:

Найти элемент, сравнивая значения узла с текущим, переходя в левое поддерево если элемент меньше и в правое, если элемент больше.

Если найденный узел не имеет дочерних узлов просто удаляем элемент.

Если имеет один дочерний узел, заменяем его на дочерний.

Если 2 дочерних узла, находим наименьший узел в правом поддереве или наибольший в левом поддереве и заменяем значение на найденный элемент, удаляя нужный узел.

После выполнения этого алгоритма требуется обновить высоты, проверить баланс и рассмотреть случаи, где баланс равен +2 или -2. (Описание аналогично вставке и написано выше).

Повороты

Правый поворот:

Правый поворот (Right Rotation) выполняется, когда узел становится несбалансированным из-за добавления узла в левое поддерево.

Определяется узел, который нужно сбалансировать Y, и его левое поддерево X.

X становится новым корнем поддерева, а Y — его правым дочерним узлом.

Левое поддерево X (если оно существует) становится правым дочерним узлом Y.

Обновляются высоты Y и X.

Левый поворот:

Левый поворот (Left Rotation) выполняется, когда узел становится несбалансированным из-за добавления узла в правое поддерево.

Определяется узел, который нужно сбалансировать Y, и его правое поддерево X.

X становится новым корнем поддерева, а Y — его левым дочерним узлом.

Правое поддерево X (если оно существует) становится левым дочерним узлом Y.

Обновляются высоты Y и X.

Верхняя оценка высоты AVL - Tree

Связь между числом узлов 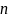и высотой :

,

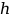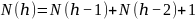Где 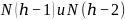- минимальное число узлов с высотой h-2 и h-1,

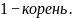
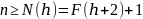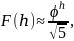
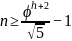
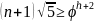
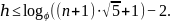
Заметим, что - числа Фибоначч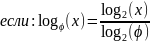и.

и 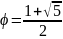тогда:

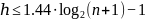
Тогда итоговая оценка будет равна: