Магнитное поле движущегося точечного заряда
Магнитное поле можно определить как отношение магнитное силы к величине элементарного тока
-
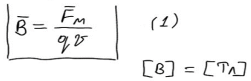
это магнитная индукция, которая является
силовой характеристикой поля, величина
векторная. Напряженность магнитной
поля присвоена вспомогательной величине
H, аналогичной вспомогательной
характеристике D электростатического
поля.
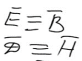
Значение индукции магнитного поля движущегося точечного заряда.
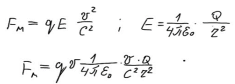
C - электродинамическая постоянная, имеющая размерность (м/с) и численно равна скорости света в вакууме
В векторном виде:
******
(не знаю, надо или нет, но немного про описание опыта:
В каждой точке пространства магн. индукция B направлена перпендикулярно плоскости, проходящей через V и данную точку пространства и направлена по правилу векторного перемножения векторов. При движении заряда электрическое поле теряет сферическую симметрию и становится осесимметричным. Расчет с учетом релятивистских эффектов показывает, что линии поля имеют вид, приведенный на рисунке:
*******
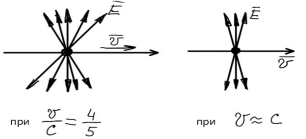
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: поле B, порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей Bi, порождаемых каждый зарядом в отдельности
Закон Био-Савара-Лапласа (при выводе закона оценка повышается очень существенно)
Закон определяет магнитное поле, создаваемое произвольным тонким проводом, по которому течет ток
Элемент dl проводника с постоянным током I создает в точке, расположенной на расстоянии r от него магнитное поле, индукция которого определяется выражением:
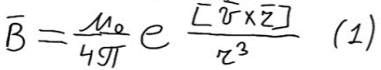
Вывод закона Био-Савара-Лапласа:
Итоговая формула:
Из (3) видно, что вектор dB направлен перпендикулярно плоскости, проходящей через dl и точку, в которой вычисляется поле. Модуль определяется выражением:
Применение закона Био-Савара-Лапласа (вывод формул поля бесконечно длинного проводника с током; поле кругового тока)
ПРИМЕР 1. Поле бесконечно длинного прямолинейного проводника с током
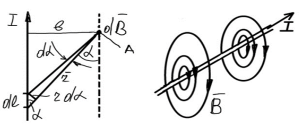
Вывод формулы:
ПРИМЕР 2. Поле кругового тока (витка с током радиусом R)
Вывод формулы:
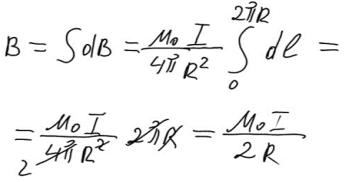
Закон Ампера (сила взаимодействия двух параллельных проводников с токами). Сила Лоренца
Закон Ампера:
На
dL в магнитном поле действует
сила:
Модуль силы:
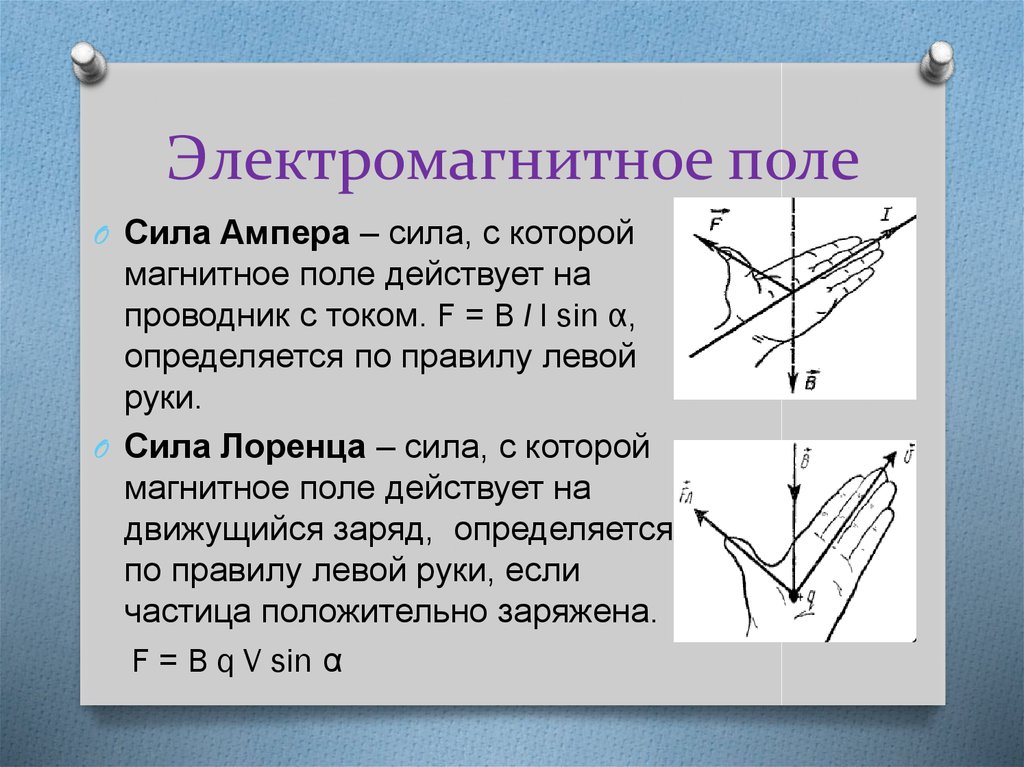
Сила Ампера направлена перпендикулярно плоскости, в которой лежат dL и B. Но можно использовать и правило левой руки.
Рисунок действия силы Ампера:
Сила взаимодействия двух параллельных проводников с токами:
Если два параллельных прямолинейных проводника расположены на расстоянии d друг от друга и по ним текут токи I1 и I2, то сила взаимодействия на единицу длины F/L между этими проводниками определяется следующим образом:
Сила Лоренца:
Из определения
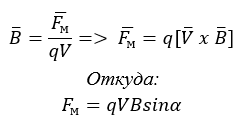
Тогда сила Лоренца:
Связь между силой Лоренца и силой Ампера:
Так как вектор магнитной силы перпендикулярен вектору скорости, то она не совершает работу. Следовательно, действиями на заряженную частицу постоянным магнитным полем нельзя изменить ее энергию.
Закон полного тока (при полном выводе формулы в интегральной форме оценка повышается). Дифференциальная форма закона
Так как в природе отсутствуют магнитные заряды, то поток вектора магнитной индукции B через замкнутую поверхность равен 0. Таким образом для любого магнитного поля и для любой замкнутой поверхности:
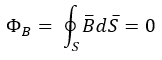
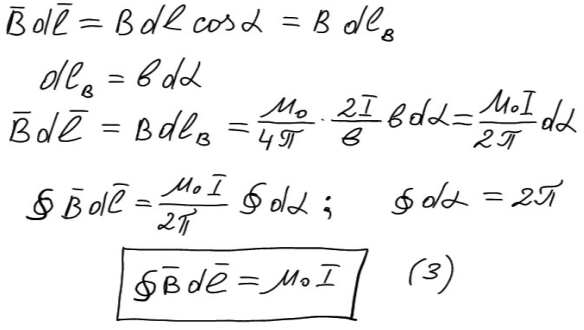
Закон полного тока:
- интегральная
форма
- дифф. форма
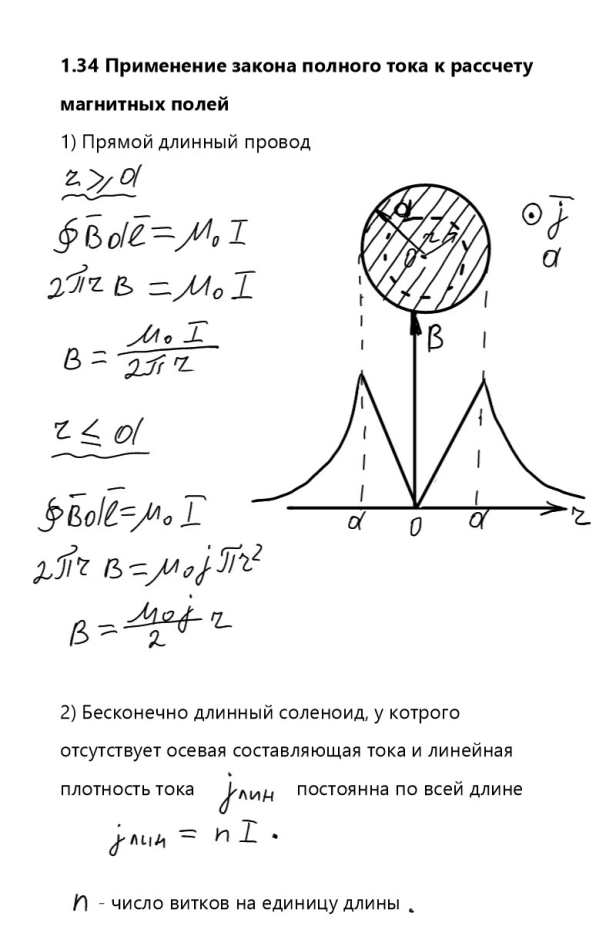
Применение закона полного тока к расчету магнитных полей (не менее двух примеров расчета)
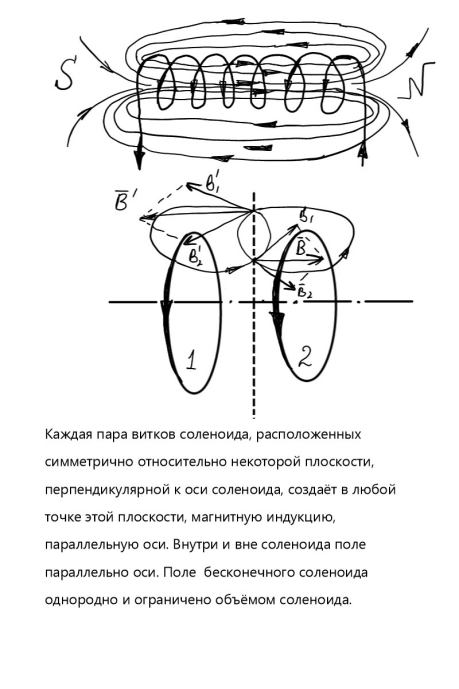
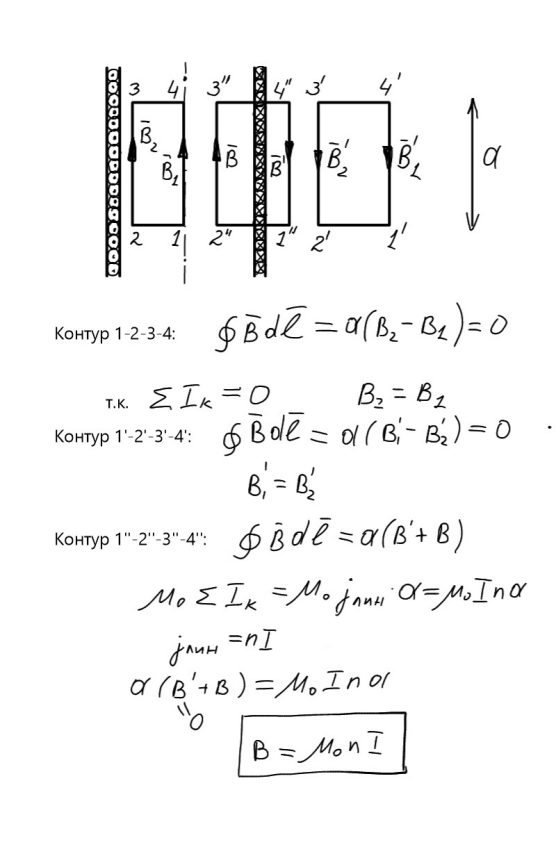
Магнитный поток. Механическая работа в магнитном поле
Формула магнитного потока:
Магнитный поток - это полное число всех силовых линий B, проходящих через поверхность S
Механическая работа в магнитном поле:
- в общем случае
- в случае, если
проводник совершает конечное перемещение.
Закон электромагнитной индукции Фарадея. Правило Ленца. ЭДС индукции. Запись закона для переменного магнитного поля Максвеллом
Закон Фарадея:
В замкнутом проводящем контуре при изменении магнитного потока магнитной индукции через поверхность, ограниченную этим этим контуром, возникает электрический ток
Явление самоиндукции. Взаимная индукция
Взаимная инд
Индуктивность????????????
Энергия магнитного поля
При замкнутой цепи в соленоиде устанавливается ток, который обуславливает МП, сцепленное с витками соленоида. Если разомкнуть ключ, то через сопротивление R некоторое время будет течь убывающий ток вследствие действия ЭДС самоиндукции. Работа, совершаемая эти током за время dt:
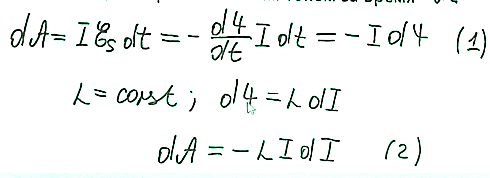
Проинтегрировав это выражение, получаем работу, совершаемую за все время, в течение которого происходит исчезновение МП
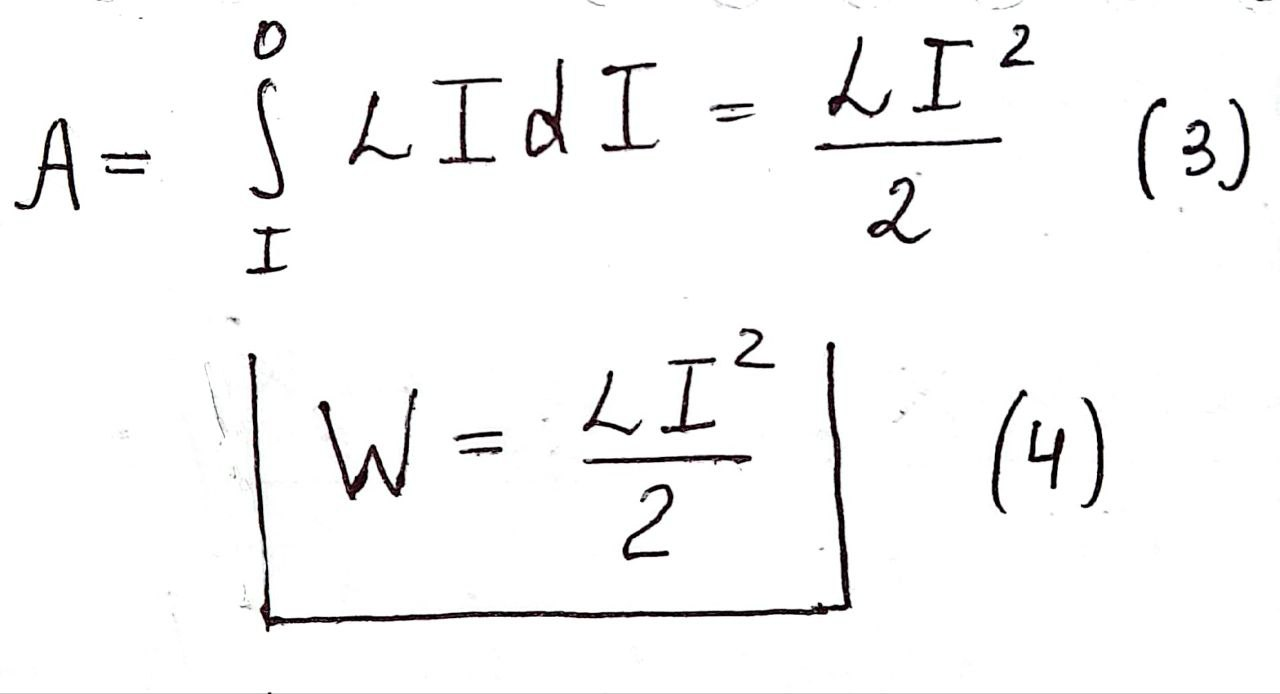
В случае бесконечно длинного соленоида:
Плотность энергии МП:
Эта энергия локализована в возбуждаемом током магнитное поле