1. Закон Кулона. Закон сохранения заряда

Точечный заряд - это заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.

Закон Кулона: два точечных неподвижных электрических заряда взаимодействуют в вакууме с силой, пропорциональной произведению модулей этих зарядов и обратно пропорциональной квадрату расстояния между ними:

Закон сохранения заряда: Заряд электростатической изолированной системы остается неизменным.

Объём шара V = 4/3 * πR³

Плоскость шара S = 4πR²

2. Электрическое поле. Напряженность поля

Взаимодействие между электрическими зарядами осуществляется через электрическое поле. Электрический заряд меняет свойство пространства вокруг себя.

Электрическое поле — это физическое поле, которое окружает каждый электрический заряд и оказывает силовое действие на другие заряды, притягивая их к заряду-источнику или отталкивая от него.

Напряженность поля - отношение силы, действующей на единичный положительный заряд, помещенный в данную точку пространства, к величине этого заряда.

q₀ - пробный заряд

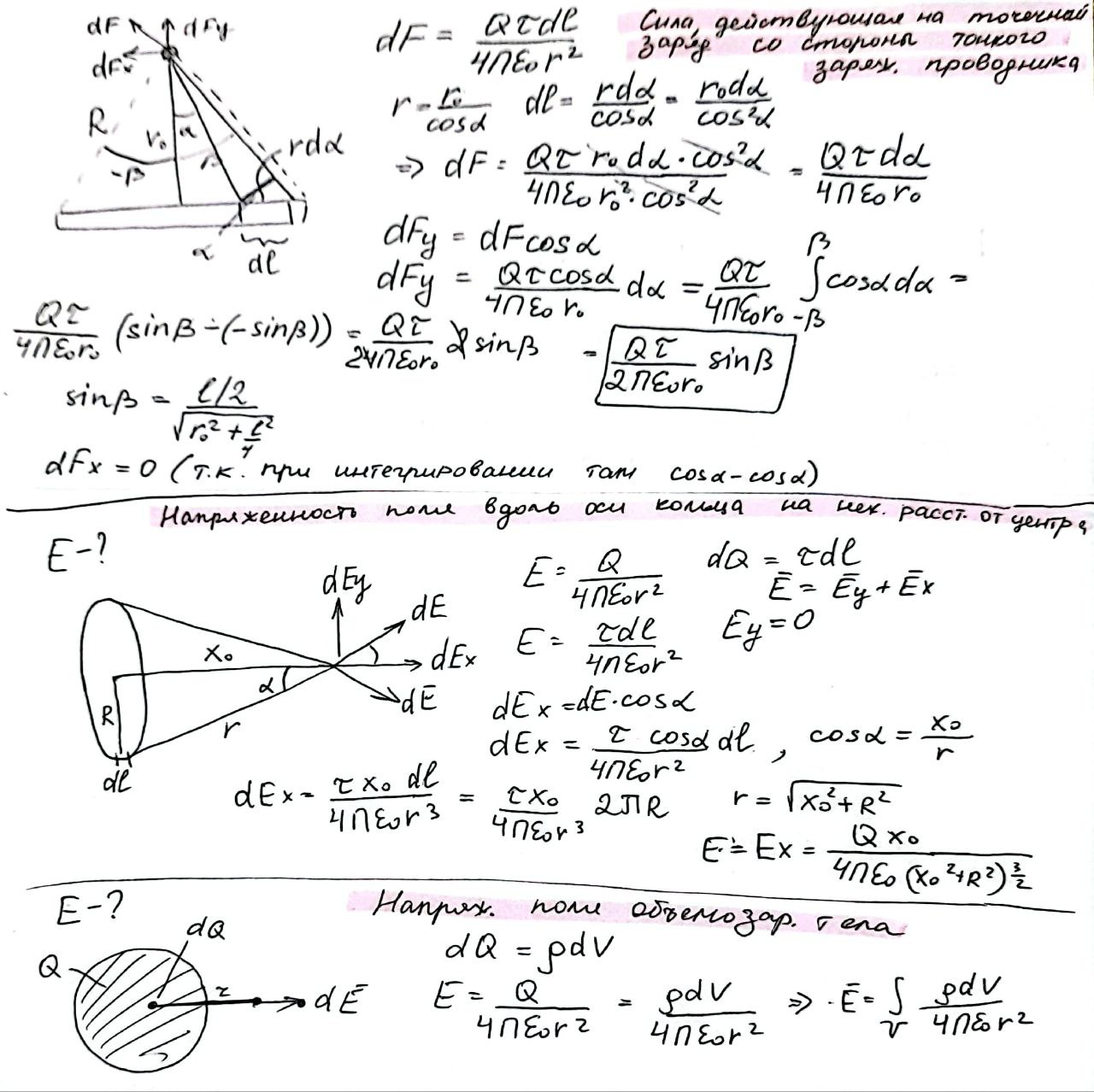
3. Расчет сил взаимодействия и напряженности полей для распределенных зарядов в электростатике (не менее двух примеров решения из лекции)

4. Поток вектора напряженности электрического поля и поток вектора электрического смещения. Теорема Остроградского-Гаусса (с доказательством)

1.Вектор электрического смещения или вектор электрической индукции (вспомогательная величина)

Виды полей

2. Поток электрического смещения d (вектора) и поток вектора напряженности поля e (вектора)

Теорема Остроградского-Гаусса для векторов D и E

5. Вычисление полей с помощью теоремы Гаусса (примеры для линейно распределенных, поверхностно распределенных и объемно распределенных зарядов)

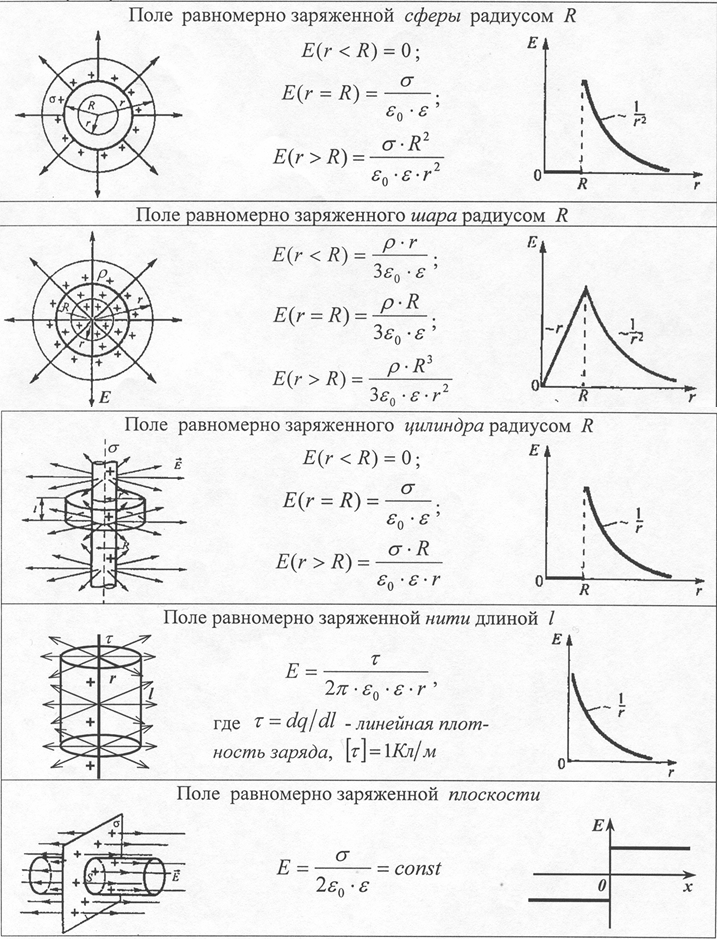
Вычисление полей с помощью теоремы Гаусса

ПРИМЕР 1. Равномерно-заряженная плоскость

ПРИМЕР 2. Поверхность заряженного проводника

6. Теорема Гаусса в дифференциальной форме

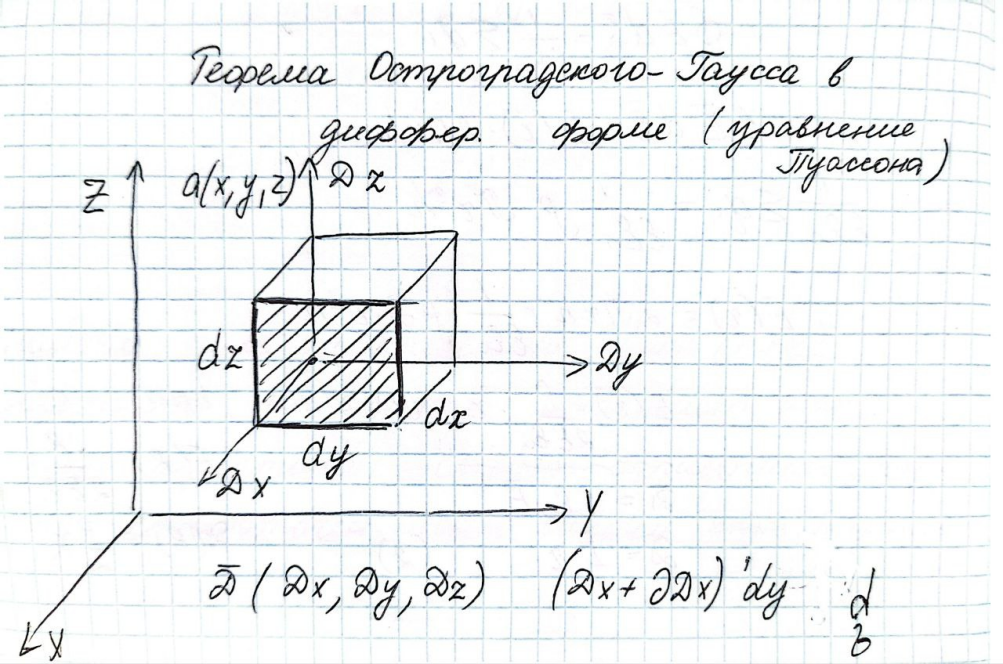
4 случая

Если в рассматриваемом объеме есть распределенный заряд с объемной плотностью, то заряд q:

7. Потенциал электрического поля

1.Работа по перемещению заряда в центральном поле сил

2.Определение потенциала. Физический смысл потенциала

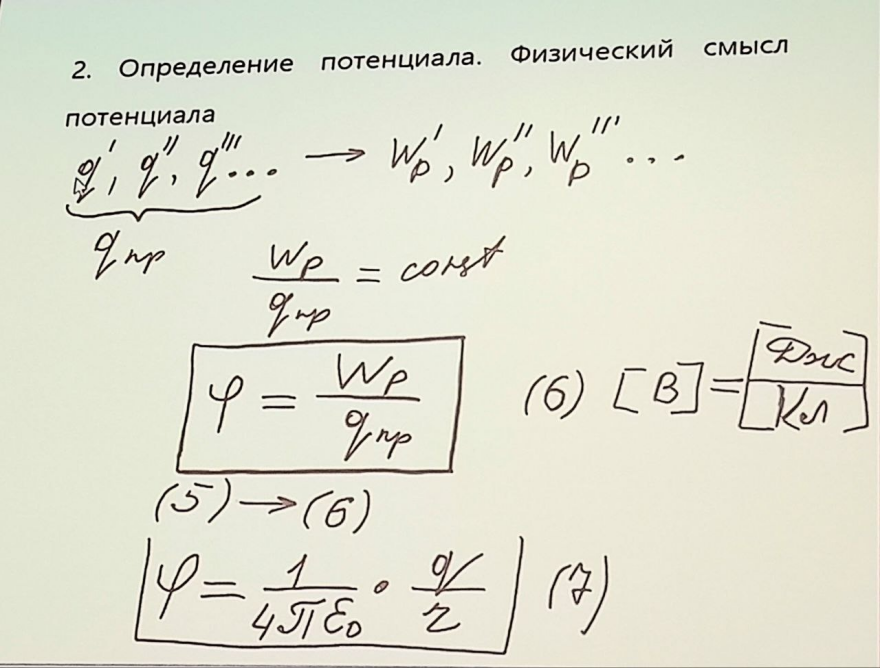
8. Потенциал в простейших электрических полях. (Точечных заряд, шаровой конденсатор, цилиндрический конденсатор, плоский конденсатор, потенциал и поле диска)

1.Потенциал точечного заряда

2.Шаровой конденсатор

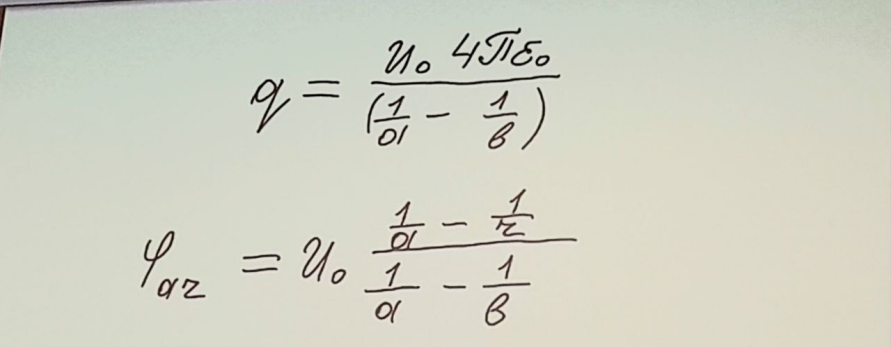
3.Плоский конденсатор

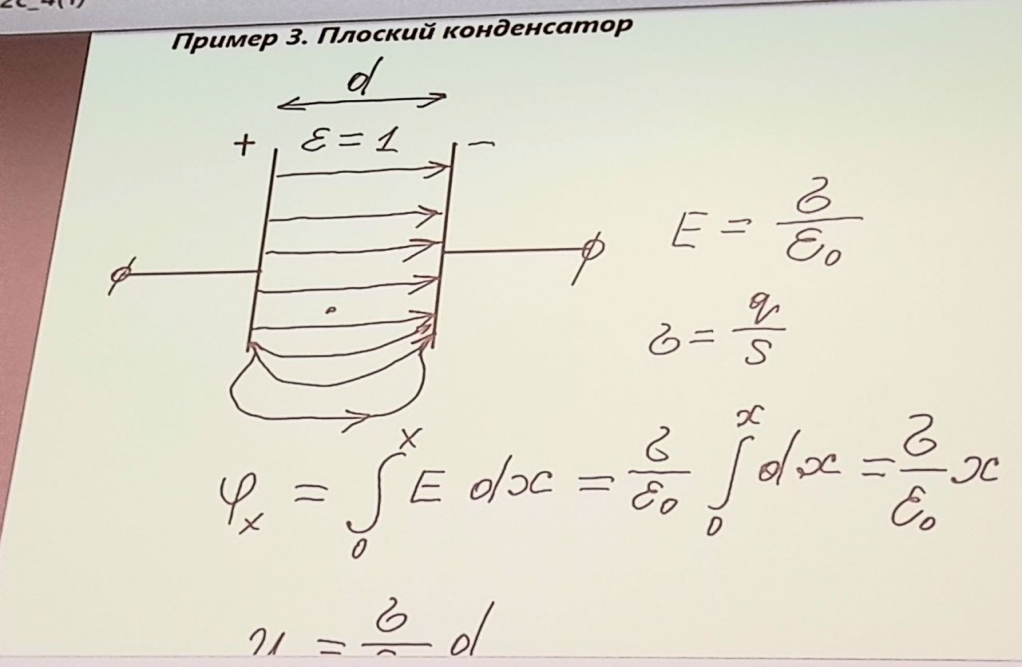
4.Цилиндрический конденсатор

5.Потенциал и поле диска

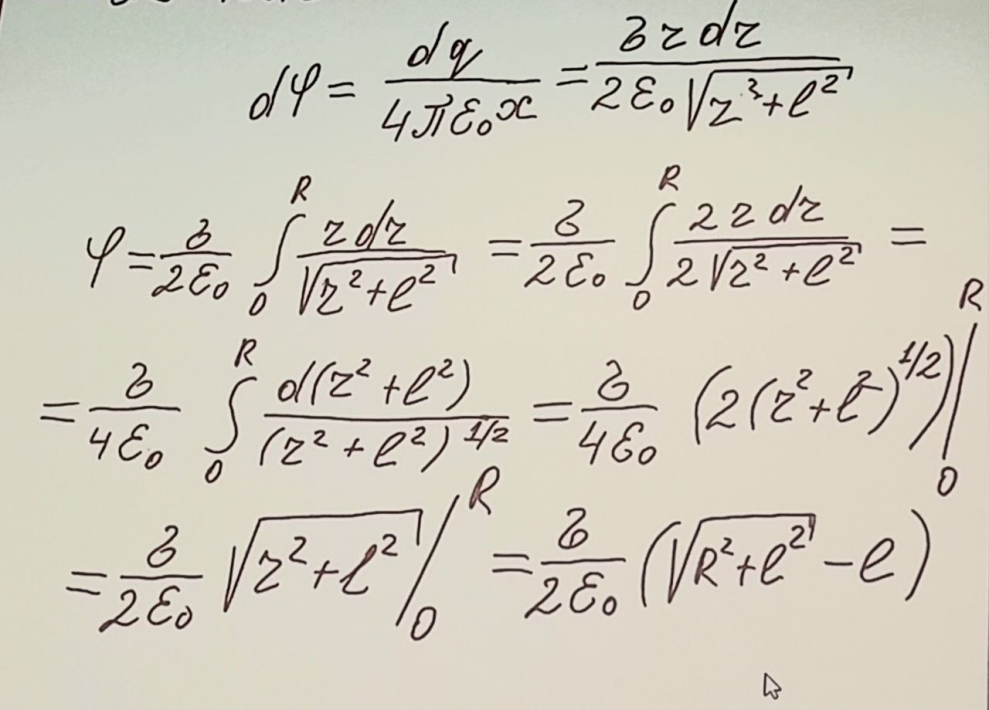
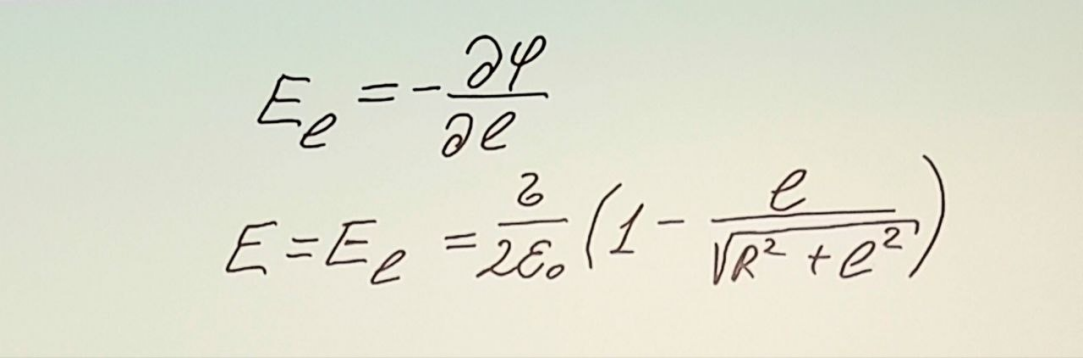
9. Связь между напряженностью электрического поля и потенциала. Циркуляция вектора Е в электростатическом поле

1.Связь между напряженностью поля и потенциалом

2. Циркуляция вектора напряженности электрического поля

Теорема о циркуляции вектора Е: Циркуляция вектора напряженности электростатического поля по замкнутому контуру равна нулю.

10. Равновесие зарядов в проводнике. Проводники в электрическом поле

Свободные носители в проводнике способны перемещаться под действием сколь угодно малой силы. Для равновесия зарядов в проводнике необходимо выполнение 2-ух условий:

1. Напряженность поля внутри пр-ка должна быть равна нулю, а, соответственно, потенциал должен оставаться неизменным;

2. Напряжённость поля на поверхности проводника в любой точке должна быть перпендикулярна поверхности пр-ка.

Рассмотрим, как распределяется по проводнику сообщенный ему заряд q? Заряд распределяется так, чтобы соблюдались условия равновесия. Выделим внутри пр-ка некоторую замкнутую поверхность и запишем теорему О.-Г.

Следовательно, избыточного заряда ни в каком месте внутри объема проводника нет, а все заряды распределяются только на поверхности пр-ка

Если убрать часть внутреннего объема заряженного пр-ка, то это не скажется на распределении зарядов:

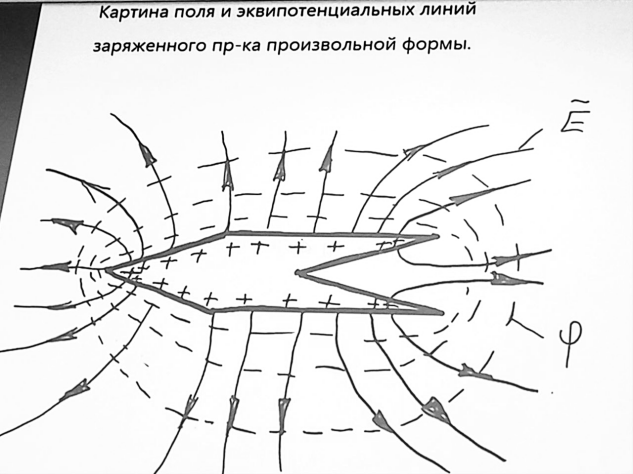
Картина поля и эквипотенциальных линий заряженного пр-ка произвольной формы

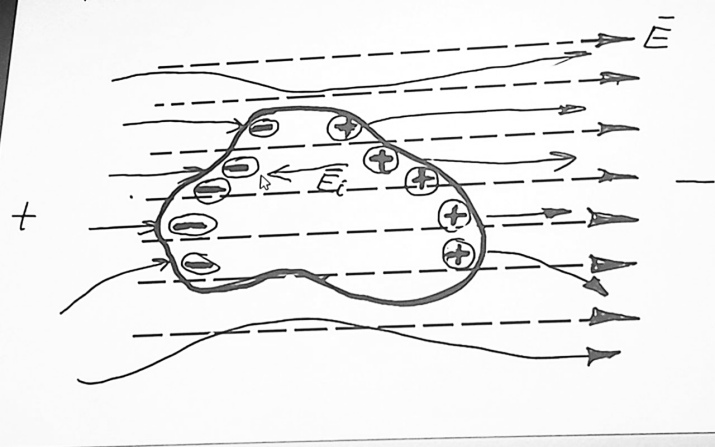
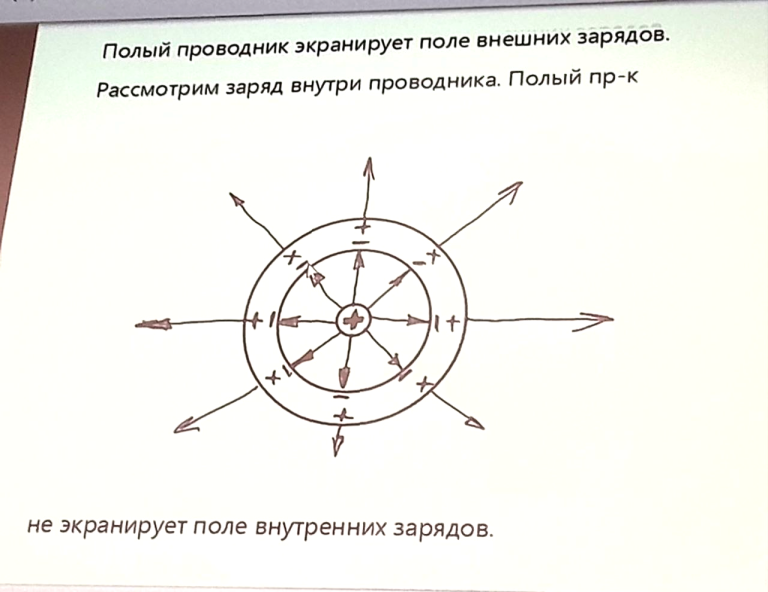
Полый проводник экранирует поле внешних зарядов. Рассмотри заряд внутри проводника. Полый проводник не экранирует поле внутренних зарядов.