_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра САПР

отчет

по лабораторной работе №1

по дисциплине «Алгоритмы и структуры данных»

Тема: Алгоритмы сжатия без потерь

Студентка гр. 3352
Преподаватель

Санкт-Петербург

2025

Цель работы: реализация алгоритмов сжатия данных.

Задачи для теоретической части:

Даны следующие алгоритмы сжатия: HA (Huffman's algorithm, алгоритм Хаффмана), BWT (Burrows-Wheeler transform, преобразование Барроуза-Уилера), MTF (Move-to-front), RLE (Run-length encoding), LZ77, LZ78.

1. Описать алгоритм

2. Написать временную и пространственную сложность.

Задачи для практической части:

1. Реализовать алгоритмы: HA, BWT, MTF, RLE, LZ77, LZ78.

2. Исследовать зависимость энтропии от размера блоков, на которые разбивается текст, подаваемый на вход BWT+MTF, для enwik7. Вывести полученные результаты на график и сделать вывод об оптимальном размере блока.

3. Исследовать зависимость коэффициента сжатия от размера буфера для алгоритма LZ77 (LZSS). Вывести полученные результаты на график и сделать вывод об оптимальном размере буфера.

4. Собрать на основе реализованных алгоритмов следующие компрессоры:

1. HA

2. Run-length encoding (RLE)

3. BWT + RLE

4. BWT + MTF + HA

5. BWT + MTF + RLE + HA

6. LZ77

7. LZ77 + HA

8. LZ78

9. LZ78 + HA

5. Удостовериться в корректной компрессии и декомпрессии данных.

6. Исследовать эффективность компрессоров для всех тестовых данных.

7. Свести результаты в виде коэффициента сжатия для каждого компрессора и всех тестовых данных в таблицы. В таблице указать размер до компрессии, после компрессии и после декомпрессии в байтах, коэффициент сжатия. Коэффициент сжатия округлить до трех цифр после запятой.

Теоретическая часть

1. Huffman’s algorithm (Алгоритм Хаффмана)

Алгоритм Хаффмана — это алгоритм сжатия данных без потерь. Идея состоит в том, чтобы присваивать входным символам коды переменной длины, длина которых зависит от частоты встречаемости соответствующих символов.

Рассмотрим кодирование слова “robot”:

1. Сначала необходимо определить частоту появления каждого символа в исходных данных.

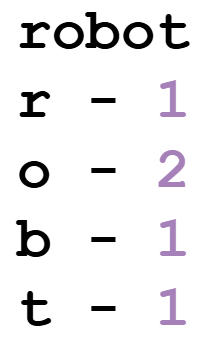
2. На основе частот строится двоичное дерево. Каждый символ становится листом дерева. Символы с наименьшей частотой объединяются, создавая новый узел, и процесс повторяется, пока не останется один узел, который станет корнем дерева.

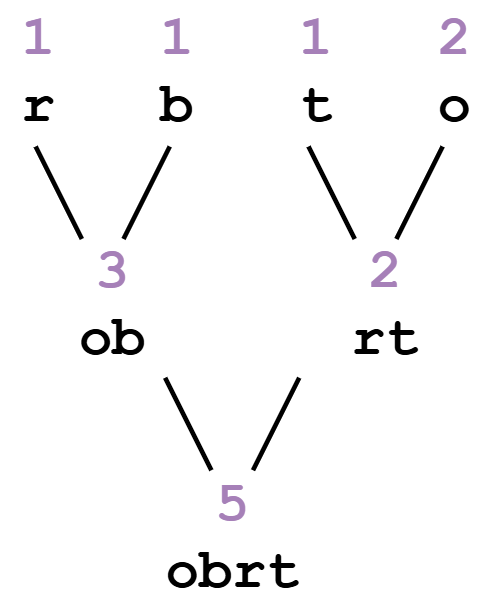
3. После построения дерева каждому символу присваивается уникальный двоичный код. Путь от корня дерева до листа определяет код: движение влево соответствует добавлению 0, а вправо — 1.

4. Исходные данные заменяются на соответствующие коды, что позволяет сократить размер файла. Код дополняется справа нулями для выравнивания до целых байтов

Декодирование: Сравниваем полученные данные с таблицей кодов и записываем соответствующие символы. Так как используются префиксные коды, декодирование всегда однозначно.

Оценка временной сложности:

Для создания словаря частот происходит проход по символам входных данных длиной n, временная сложность - 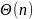. На построение двоичного дерева уходит 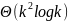, где k - количество уникальных символов. Для построения кодовой таблицы нужно пройти по дереву один раз, что значит 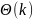. Итоговая временная сложность .

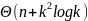Оценка пространственной сложности:

Для хранения словаря уникальных символов нужно . Хранение узлов дерева и кодовой таблицы занимает столько же, . На хранение закодированных данных нужно 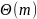, где m - длина закодированных данных. Итоговая пространственная сложность .

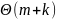2. Bwt (Преобразование Барроуза-Уилера)

Преобразование Барроуза-Уилера - это алгоритм, который используется для преобразования строки в такую форму, которая более эффективно поддается сжатию. Он не является методом сжатия сам по себе, но создает структуру данных, которую можно эффективно сжимать с помощью других алгоритмов.

Для преобразования данные для начала делятся на блоки заданной длины, после чего происходит изменение каждого блока. Рассмотрим преобразования для того же слова ‘robot’:

1. Для строки (блока) составляется список всех возможных циклических перестановок. Например, перемещаем первый символ в конец, а остальные символы сдвигаем влево.

2. Получившийся список (массив) сортируем. Сначала сортировка происходит по первому символу, для тех строк, где первый символ совпадает - по второму, и т.д.

3. Записываем последний столбец и индекс исходной строки.

Обратное преобразование:

1. Отсортируем символы полученного столбца (получился первый столбец матрицы циклических перестановок)

2. Символы последнего и первого столбца образуют пары, которые мы сортируем по возрастанию. Добавляя каждый раз последний символ в начало строки и сортируя снова все строки, получаем первоначальную матрицу. По индексу находим нужную строку.

Оценка временной сложности:

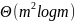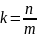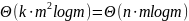Рассмотрим временную сложность для обработки одного блока: генерация циклических сдвигов занимает , где m - размер блока; сортировка сдвигов - ; поиск индекса нужно строки - ; сбор последнего столбца - . Итоговая временная сложность составляет для одного блока. Так как данные делятся на блоков заданной длины m, то общая временная сложность . Декодирование для одного блока займет , так как сортируются символы только последнего столбца длиной n, значит для для всех блоков .

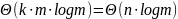Оценка пространственной сложности:

Для одного блока: хранение циклических и отсортированных сдвигов - . Хранение преобразованных данных - ; хранение индексов - . Итого: 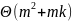= . Для декодирования потребуется 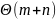? так как требуетс хранить только индексы и закодированную строку.

3. MTF (Move-to-front)

MTF (move-to-front, движение к началу) — алгоритм кодирования, используемый для предварительной обработки данных перед сжатием, разработанный для улучшения производительности последующего кодирования.

Кодирование:

1. Для имеющийся строки инициализируем алфавит, содержащий байты от 0 до 255. В выходной массив добавляем индекс первого символа исходного слова. Например, для слова ‘robot’ первый символ строки является элементом алфавита с индексом 114, значит выходные данные имеют вид [114].

2. Помещаем только что использованный элемент в первое место в алфавите, получаем алфавит [114,0,…255] и повторяем процесс со вторым символом. Для символа o-111 индекс в алфавите будет 112, помещаем его в выходные данные [114,112], а в алфавите индекс 111 перемещаем на первое место [111,114,0,..255]. И так далее. Получаем выходные данные [114,112,100,1,116].

Декодирование:

1. Ищем в алфавите от [0...255] элемент с индексом, равным первому элементу в закодированных данных, 114. Получаем на выходе [114], и этот символ помещается в начало алфавита [114,0,…255]. Символ с номером 112 в алфавите [114...255] - это 111, поэтому на выводе получаем [114,111] и номер 112 перемещается в начало алфавита -> [112,114,0,…255]. И так далее. Получаем строку [114,111,98,111,116], что соответствует слову robot’.

Оценка временной сложности:

Для каждого символа входных данных нужно найти символ в списке фиксированной длинны (256) и переместить его в начало списка. Общая сложность для обработки всех символов , где n - длина входных данных, тогда общая временная сложность . Декодирование займет , поскольку для каждого индекса в закодированных данных длиной n выполняется фиксированное количество итераций удаления и вставки элемента.

Оценка пространственной сложности:

Для хранения алфавита 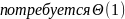, для хранения закодированных данных Итого пространственная сложность . Для декодирования она так же составит .

4. RLE (Run-length encoding)

RLE (англ. run-length encoding) — алгоритм сжатия данных, который заменяет повторяющиеся символы (серии) на один символ и число его повторов.

Кодирование:

1. Проходим по входным данным.

2. Подсчитываем количество последовательно повторяющихся символов (длину пробега).

3. Сохраняем символ и его длину выполнения.

Декодирование:

1. Проходим по закодированным данным.

2. Для каждой пары количество символов повторяем подсчёт символов несколько раз.

3. Добавляем эти символы в результирующую строку.

Оценка временной сложности:

Алгоритм проходит по входным данным один раз, сравнивая текущий символ с предыдущим. Если символ повторяется, увеличивается счётчик. Если символ меняется, записывается пара и сбрасывается счётчик. Так как алгоритм проходит по данным один раз, выполняя константное количество операций для каждого символа, итоговая временная сложность , где n - длина входных символов. Декодирование займёт де m - длина закодированных данных.

Оценка пространственной сложности:

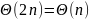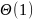В худшем случае (если нет повторяющихся символов) выходные данные могут занимать памяти (каждый символ записывается как отдельная пара. В лучшем случае выходные данные занимают памяти. Декодирование займет (исходный размер данных).

5. LZ77

LZ77 - один из наиболее простых и известных алгоритмов в семействе LZ. Основная идея заключается в том, чтобы кодировать одинаковые последовательности элементов. Т.е., если во входных данных какая-то цепочка элементов встречается более одного раза, то все последующие её вхождения можно заменить «ссылками» на её первый экземпляр.

Алгоритм использует так называемое "скользящее окно", которое делится на две части: буфер поиска (или "источник"), где хранятся уже обработанные данные, и буфер ввода, который содержит данные, подлежащие сжатию. Размер окна фиксирован, и оно перемещается по входным данным.

Кодирование:

1. Алгоритм ищет в буфере поиска последовательности символов, которые совпадают с символами в буфере ввода.

2. Если совпадение найдено, оно представляется в виде тройки: (дистанция, длина, следующий символ). Дистанция - количество символов, которые нужно "откатить" назад в буфере поиска для нахождения совпадения. Длина - количество символов, которые совпадают. Следующий символ - тот, который идет сразу после совпадения в буфере ввода.

3. Если совпадение не найдено, алгоритм просто записывает текущий символ как литерал. Процесс продолжается до тех пор, пока не будут обработаны все данные.

Декодирование происходит путем восстановления оригинальной строки на основе записанных троек. Используя информацию о дистанции и длине, алгоритм восстанавливает повторяющиеся последовательности.

Оценка временной сложности:

Для каждого символа выполняется поиск совпадений в окне, что занимает (w - размер окна, l - размер буфера). Всего символов n, значит общая временная сложность . Декодирование выполняется за , так как происходит однократный проход по сжатым данным.

Оценка пространственной сложности:

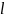Алгоритм хранит скользящее окно размером и буфер размером для входных данных размером , что требует памяти. Декодирование занимает для хранения декодированных данных.

6. LZ78

LZ78 является продолжением алгоритма LZ77 и основывается на аналогичных принципах, но имеет некоторые отличия в подходе к сжатию. Алгоритм использует динамически формируемый словарь, который хранит уникальные последовательности символов, встречающиеся в исходных данных. Каждый элемент словаря представляет собой пару: (индекс, символ), где индекс указывает на позицию предыдущей последовательности, а символ — это новый символ, который следует за этой последовательностью.

Кодирование:

1. Алгоритм читает входные данные по одному символу за раз и пытается найти наибольшую совпадающую последовательность в словаре.

2. Если совпадение найдено, алгоритм добавляет в выходной поток пару (индекс, символ), где индекс — это позиция совпадения в словаре, а символ — следующий символ, который не входит в найденную последовательность.

3. Если совпадение не найдено, алгоритм добавляет новую последовательность в словарь и записывает (0, символ), где 0 указывает на отсутствие совпадений.

Декодирование:

Читаем закодированные данные и по индексу из словаря выводим последовательность + добавляем новый символ в вывод. Если индекс равен 0 , просто добавляем символ в вывод.

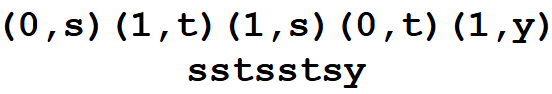
Оценка временной сложности:

Для каждого символа входных данных алгоритм проверяет, существует ли текущая подстрока в словаре - , в худшем случае может достигнуть 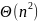, если все символы уникальны. Формирование закодированных данных требует де m - число записей в выходной массив. Декодирование так же займет .

Оценка пространственной сложности:

Для словаря, хранящего уникальные последовательности, потребуется , где k - количество последовательностей (если данные несжимаемы, оно равно n). Выходные данные займут . Итого или для худшего слушая , если данные не были сжаты. Декодирование займет .