Обработка результатов измерений

Вычислим резонансные частоты -двухполюсника, изображенного на рис. 8.1

Гн, Гн, мкФ, мкФ

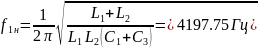
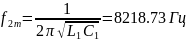
Для -двухполюсника, изображенного на рис. 8.1, б, резонансная частота

Гн, мкФ кОм или кОм

Для

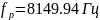
Для

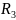
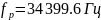
Найдем R, для которого будет возможен резонанс. Для начала рассчитаем для

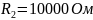
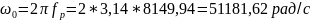
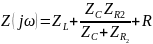
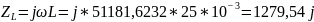
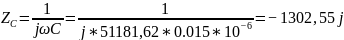
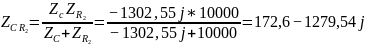
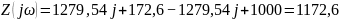
Из вычислений мы делаем вывод, что при сопротивлении резонанс возможен так как мнимая часть входного сопротивления равна нулю.

Рассчитаем для

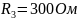
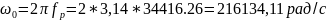
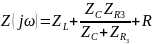
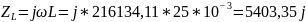
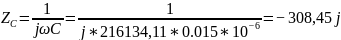
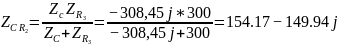
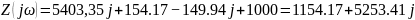
Так как мнимая часть не равна нулю резонанс в цепи невозможен.

Вывод

В ходе работы были исследованы амплитудно-частотные (АЧХ) и фазочастотные (ФЧХ) характеристики входных сопротивлений LC- и RLC-двухполюсников. Экспериментальные данные подтвердили теоретические зависимости, демонстрируя влияние элементов R, L и C на частотные характеристики двухполюсников.

Ответы на вопросы

1. В чем отличие частотных характеристик реальной цепи, составленной из катушек индуктивностей и конденсаторов, от характеристик идеальных реактивных двухполюсников?

Мнимое сопротивление идеального реактивного двухполюсника можно представить в виде 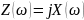, где степень мнимой части зависит от порядка резонанса. Модуль сопротивления может стремиться к бесконечности при параллельном резонансе или нулю при последовательном резонансе. В реальных цепях из-за наличия активных потерь (сопротивления проводов, диэлектрические потери) эти экстремумы не достигаются. Максимум ограничен добротностью контура, а минимум не опускается до нуля.

2.Как проконтролировать полученные АЧХ и ФЧХ по эквивалентным схемам цепи f = 0, f = , f = f_1т, f_2т?

АЧХ и ФЧХ по эквивалентным схемам пр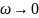и и 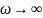. При и цепь можно анализировать через упрощённые схемы замещения:

При катушки КЗ, конденсаторы ХХ, АЧХ |Z|->0 если есть путь через катушки. При катушки ХХ, конденсаторы КЗ, АЧХ |Z|->0 если есть путь через конденсаторы. Резонансные частоты соответствуют полюсам 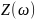, где 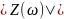имеет локальные максимумы (в идеальном случае — разрывы).

3.Можно ли по частотным характеристикам (ачх, фчх, афх) определить резонансные частоты двухполюсника? По каким признакам?

АЧХ можно определить по локальным максимумам 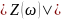, ФЧХ - по переходу фазы через ноль, АФХ можно определить по точкам пересечения с вещественной осью.

4.В чем причина отсутствия резонанса в исследуемой - цепи и, какие из графиков (ачх, фчх или афх) об этом свидетельствуют?

Резонанс отсутствует, если уравнение 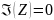не имеет действительных решений. Признаки на графиках – АЧХ – нет выраженных пиков, монотонное изменение, ФЧХ – фаза не пересекает ноль.

5. Как проконтролировать АЧХ, ФЧХ и АФХ цепи при f = 0 и f = ? Для последовательного резонанса: Z = R, АЧХ: |Z| = R, ФЧХ:

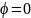
Для параллельного резонанса Z -> , АЧХ - |Z| - максимум, ФЧХ: