- •Экспериментальные исследования Исследование частотных характеристик - двухполюсника
- •Исследование частотных характеристик - двухполюсника
- •Исследование частотных характеристик rlc- двухполюсника, в котором резонанс возможен.
- •Исследование частотных характеристик rlc-двухполюсника, в котором резонанс невозможен.
- •Обработка результатов измерений
- •Ответы на вопросы
- •1. В чем отличие частотных характеристик реальной цепи, составленной из катушек индуктивностей и конденсаторов, от характеристик идеальных реактивных двухполюсников?
- •3.Можно ли по частотным характеристикам (ачх, фчх, афх) определить резонансные частоты двухполюсника? По каким признакам?
- •4.В чем причина отсутствия резонанса в исследуемой - цепи и, какие из графиков (ачх, фчх или афх) об этом свидетельствуют?
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра теоретических основ электротехники
отчет
по лабораторной работе №8
по дисциплине «ТОЭ»
Тема: Исследование частотных характеристик двухполюсников
Студентки гр. 3352 |
|
Гареева К.Р. |
|
|
Жигунова О.М. |
Преподаватель |
|
Балданова Ю.А. |
Санкт-Петербург
2025
Цель работы
Исследование
амплитудно-частотных и фазовых
характеристик входных сопротивлений
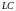 -
и
-
и
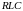 -
двухполюсников.
-
двухполюсников.
Подготовка к работе
В работе необходимо исследовать частотные характеристики реактивного LC-двухполюсника и RLC-двухполюсника, схемы которых представлены на рис. 8.1.
При действии на цепь источника тока реакцией на входе является напряжение и свойства пассивного двухполюсника (ДП) в установившемся синусоидальном режиме определяются входным сопротивлением
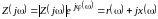 .
.
График
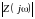 ,
построенный в функции частоты ,
является в данном случае амплитудно-частотной
характеристикой (АЧХ), график аргумента
()
– фазочастотной характеристикой (ФЧХ),
а графики
,
построенный в функции частоты ,
является в данном случае амплитудно-частотной
характеристикой (АЧХ), график аргумента
()
– фазочастотной характеристикой (ФЧХ),
а графики
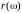 и
и
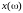 – соответственно вещественной и мнимой
частотными характеристиками двухполюсника.
Используют также амплитудно-фазовую
характеристику (АФХ), представляющую
собой геометрическое место значений
– соответственно вещественной и мнимой
частотными характеристиками двухполюсника.
Используют также амплитудно-фазовую
характеристику (АФХ), представляющую
собой геометрическое место значений
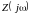 ,
построенное в комплексной плоскости,
например по графикам АЧХ и ФЧХ.
,
построенное в комплексной плоскости,
например по графикам АЧХ и ФЧХ.
При резонансе в пассивном двухполюснике
выполняются условия
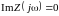 и
и
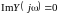 ,
т. е. на резонансной частоте
,
т. е. на резонансной частоте
 в установившемся синусоидальном режиме
ток и напряжение двухполюсника совпадают
по фазе:
в установившемся синусоидальном режиме
ток и напряжение двухполюсника совпадают
по фазе:
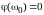 .
.
Для
 -
двухполюсника входное сопротивление
будет мнимой дробно-рациональной
функцией вида:
-
двухполюсника входное сопротивление
будет мнимой дробно-рациональной
функцией вида:
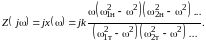 (8.1)
(8.1)
Нули
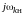 и полюсы
и полюсы
 сопротивления
сопротивления
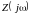 ,
определяемые соответственно из условия
резонанса напряжений
,
определяемые соответственно из условия
резонанса напряжений
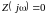 и условия резонанса токов
и условия резонанса токов
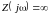 ,
совпадают с резонансными частотами
-
двухполюсника. Они являются мнимыми
числами и располагаются, чередуясь друг
с другом, на оси
,
совпадают с резонансными частотами
-
двухполюсника. Они являются мнимыми
числами и располагаются, чередуясь друг
с другом, на оси
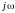 плоскости комплексной частоты
плоскости комплексной частоты
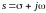 .
В зависимости от структуры и элементов
цепи в начале координат располагается
либо нуль, как в (8.1), либо полюс.
.
В зависимости от структуры и элементов
цепи в начале координат располагается
либо нуль, как в (8.1), либо полюс.
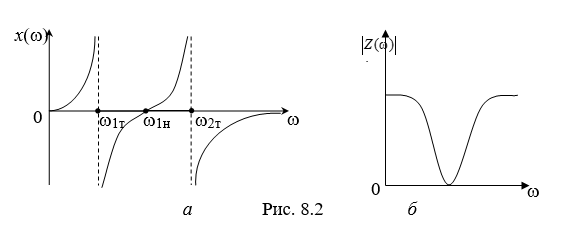
Используя указанные свойства реактивных
двухполюсников, а также свойство dx/d
0, можно построить
частотные характеристики jx()
качественно. Например, для двухполюсника,
изображенного на рис. 8.1, а, частотная
характеристика jx(),
приведенная на рис. 8.2, а, может быть
построена качественно для
> 0 исходя из следующих соображений: в
цепи возможны лишь 3 резонансные частоты
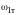 ,
,
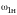 и
и
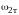 ;
предельные значения сопротивления x(0)
= 0 и
;
предельные значения сопротивления x(0)
= 0 и
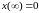 оцениваются путем анализа эквивалентной
схемы замещения при
= 0 и
.
оцениваются путем анализа эквивалентной
схемы замещения при
= 0 и
.
Амплитудно-частотная характеристика
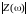 этого идеализированного LC-двухполюсника
определяется модулем функции, изображенной
на рис. 8.2, а, поскольку
этого идеализированного LC-двухполюсника
определяется модулем функции, изображенной
на рис. 8.2, а, поскольку
 .
АЧХ двухполюсника с реальными катушками
индуктивности и конденсаторами,
полученная опытным путем, не принимает
нулевых и бесконечно больших значений;
она является непрерывной функцией
частоты, но при высокой добротности
контуров, исследуемых в работе (Q
15…20), сохраняет большую крутизну в
области резонансных значений частоты.
.
АЧХ двухполюсника с реальными катушками
индуктивности и конденсаторами,
полученная опытным путем, не принимает
нулевых и бесконечно больших значений;
она является непрерывной функцией
частоты, но при высокой добротности
контуров, исследуемых в работе (Q
15…20), сохраняет большую крутизну в
области резонансных значений частоты.
Для
-
двухполюсника в зависимости от соотношения
значений параметров
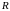 ,
,
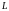 ,
,
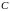 резонанс может и не наблюдаться. Следует
также отметить, что в
-
двухполюсниках частоты, соответствующие
максимальным
резонанс может и не наблюдаться. Следует
также отметить, что в
-
двухполюсниках частоты, соответствующие
максимальным
и минимальным значениям
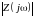 ,
в общем случае не совпадают с резонансными.
,
в общем случае не совпадают с резонансными.
1. Вычислите резонансные частоты
-двухполюсника,
изображенного на рис. 8.1, а (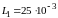 Гн,
Гн,
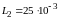 Гн,
Гн,
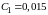 мкФ,
мкФ,
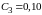 мкФ), по формулам:
мкФ), по формулам:
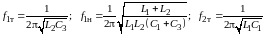 (8.2)
(8.2)
и постройте качественно график АЧХ двухполюсника.
2. Для -двухполюсника, изображенного на рис. 8.1, б, резонансная частота
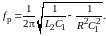 (8.3)
(8.3)
Приняв
Гн,
мкФ выясните, при каком из значений
резистора R, (используемых
в работе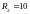 кОм
или
кОм
или
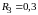 кОм), резонанс невозможен, а при каком
возможен; вычислите на основании (8.3)
значение резонансной частоты и постройте
качественно АЧХ
-
двухполюсника для обоих случаев.
кОм), резонанс невозможен, а при каком
возможен; вычислите на основании (8.3)
значение резонансной частоты и постройте
качественно АЧХ
-
двухполюсника для обоих случаев.
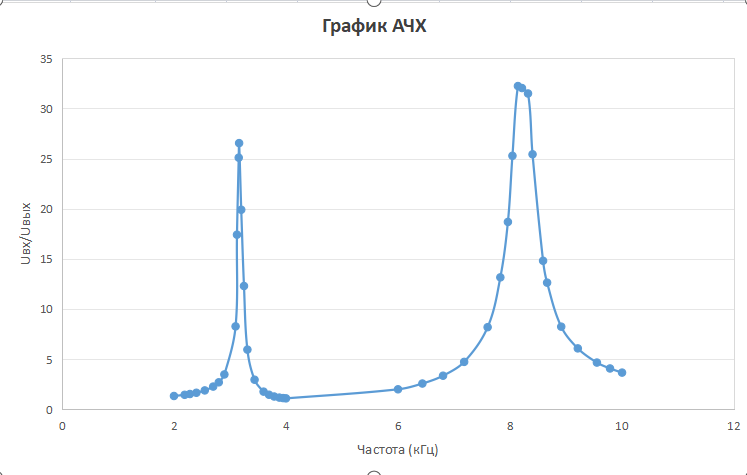
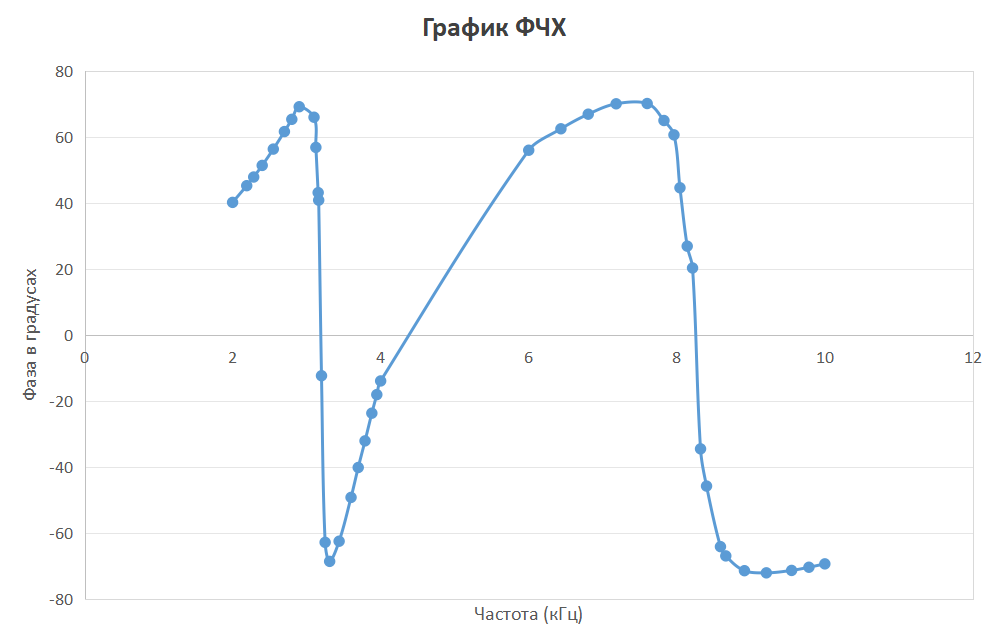
Экспериментальные исследования Исследование частотных характеристик - двухполюсника
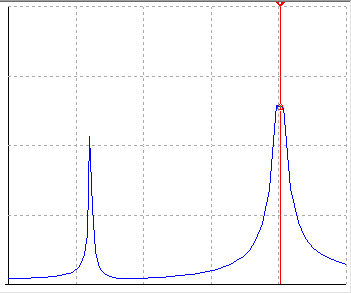
f1t, кГц |
3.167 |
max |
f1н, кГц |
4.191 |
min |
f2t, кГц |
8.222 |
max |
Исследование частотных характеристик - двухполюсника
|
UВХ/UR1 |
,° |
|Z|, Ом |
2 |
1,322 |
40,157 |
1322 |
2,191 |
1,44 |
45,223 |
1440 |
2,285 |
1,52 |
47,846 |
2520 |
2,4 |
1,644 |
51,364 |
1644 |
2,55 |
1,878 |
56,3152 |
1878 |
2,7 |
2,261 |
61,624 |
2261 |
2,8 |
2,686 |
65,339 |
2686 |
2,9 |
3,472 |
69,156 |
7250 |
3,1 |
8,26 |
65,973 |
8266 |
3,125 |
17,41 |
56,828 |
17410 |
3,156 |
25,092 |
43,109 |
25092 |
3,163 |
26,545 |
40,825 |
26545 |
3,201 |
19,897 |
-12,393 |
19897 |
3,25 |
12,291 |
-62,905 |
12291 |
3,311 |
5,946 |
-68,673 |
5946 |
3,439 |
2,945 |
-62,566 |
12945 |
3,6 |
1,756 |
-49,279 |
1756 |
3,697 |
1,447 |
-40,214 |
1447 |
3,789 |
1,270 |
-32,147 |
1270 |
3,881 |
1,162 |
-23,752 |
1162 |
3,948 |
1,114 |
-18,123 |
1114 |
4 |
1,086 |
-13,977 |
1086 |
6 |
1,99 |
55,969 |
1990 |
6,435 |
2,565 |
62,469 |
2565 |
6,804 |
3,345 |
66,897 |
3345 |
7,181 |
4,724 |
70,043 |
4724 |
7,6 |
8,185 |
70,129 |
8185 |
7,827 |
13,154 |
64,976 |
13154 |
7,962 |
18,683 |
60,631 |
18683 |
8,043 |
25,279 |
44,591 |
25279 |
8,141 |
32,236 |
26,885 |
32236 |
8,213 |
32,036 |
2027 |
32036 |
8,321 |
31,494 |
-34,568 |
31494 |
8,402 |
25,43 |
-45,844 |
25430 |
8,59 |
14,808 |
-64,215 |
14808 |
8,662 |
12,626 |
-67,016 |
12626 |
8,914 |
8,236 |
-71,5 |
8236 |
9,21 |
6,07 |
-72,154 |
6070 |
9,551 |
4,656 |
-71,42 |
4656 |
9,785 |
4,067 |
-70,456 |
4067 |
10 |
3,655 |
-69,435 |
3655 |