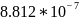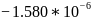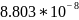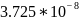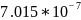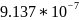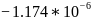Экспоненциальный поиск
Для экспериментальной оценки временной сложности интерполяционного поиска было сделано 21 измерение для массивов длиной от 1 до 100001 элементов с шагом в 5000.
Таблица - Экспериментальные значения для экспоненциального поиска
Длина массива |
Лучший |
Средний |
Худший |
1 |
2.119992859661579e-07 |
9.799958206713199e-08 |
1.0099727660417556e-07 |
2501 |
3.839971031993628e-07 |
2.2810010705143215e-06 |
2.6360072661191226e-06 |
5001 |
2.8299284167587756e-07 |
2.895002253353596e-06 |
3.4190004225820305e-06 |
7501 |
3.809994086623192e-07 |
3.7049944512546062e-06 |
4.083001986145973e-06 |
10001 |
4.030007403343916e-07 |
3.5560026299208405e-06 |
4.390992689877748e-06 |
12501 |
4.630000330507755e-07 |
4.176007350906729e-06 |
4.7489930875599385e-06 |
15001 |
5.159981083124876e-07 |
4.363000625744462e-06 |
5.145996110513806e-06 |
17501 |
5.139946006238461e-07 |
4.394002025946975e-06 |
5.181995220482349e-06 |
20001 |
5.670019891113043e-07 |
4.8720056656748055e-06 |
5.720991175621748e-06 |
22501 |
5.239981692284345e-07 |
5.173996323719621e-06 |
5.858996883034706e-06 |
25001 |
5.939987022429704e-07 |
5.122990114614368e-06 |
5.985997850075364e-06 |
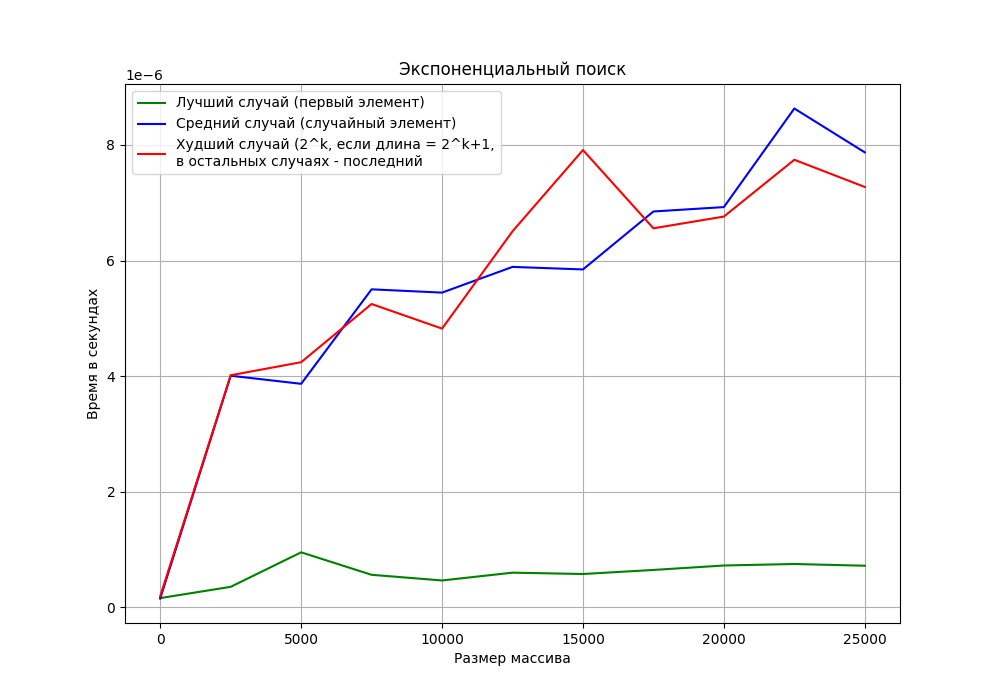
Рисунок - График временной сложности экспоненциального поиска с экспериментальными значениями.
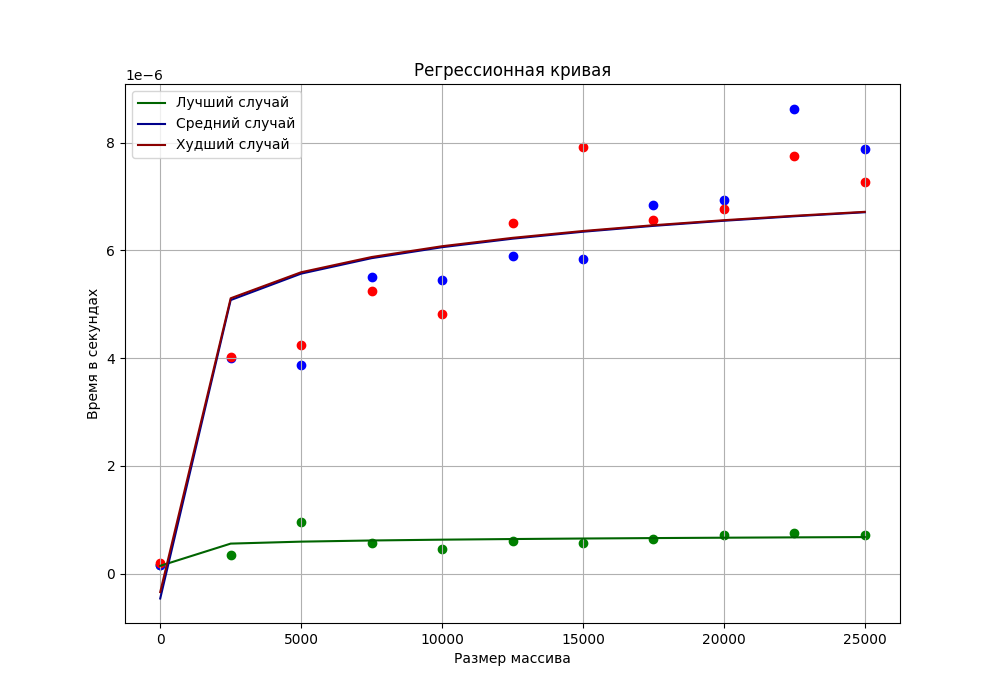
Рисунок - График экспериментальных значений с регрессионной кривой.
Рисунок - График временной сложности из теоритической части.
Таблица - Коэффициенты моделей для экспоненциальный поиска
Случай |
Модель |
Коэффициенты |
|
|
|
||
Лучший |
=a 1+b |
|
|
Средний |
=a logn+b |
|
|
Худший |
=a logn+b |
|
|
Сравнив график с регрессией и график из теоретической части, мы можем сделать вывод, что асимптотика для всех трех случаев в экспериментальной части согласуется с теоретической асимптотикой временной сложности: прямая для лучшего случая и логарифмическая для среднего и худшего случаев.
Фибоначчиев поиск
Для экспериментальной оценки временной сложности Фибоначчиева поиска было сделано 21 измерение для массивов длиной от 1 до 100001 элементов с шагом в 5000.
Таблица - Экспериментальные значения для Фибоначчиева поиска
Длина массива |
Лучший |
Средний |
Худший |
1 |
4.2000319808721544e-07 |
3.400025889277458e-07 |
3.2000243663787844e-07 |
2501 |
5.170004442334175e-06 |
4.640023689717054e-06 |
2.420006785541773e-06 |
5001 |
6.079976446926594e-06 |
6.730039604008198e-06 |
1.640012487769127e-06 |
7501 |
6.2500126659870144e-06 |
7.5899763032794e-06 |
1.8200138583779334e-06 |
10001 |
5.929986946284771e-06 |
6.190012209117413e-06 |
2.580008003860712e-06 |
12501 |
4.560023080557585e-06 |
7.489998824894428e-06 |
3.3999676816165447e-06 |
15001 |
3.389979247003794e-06 |
6.6300155594944956e-06 |
3.740005195140839e-06 |
17501 |
4.249997437000274e-06 |
7.249973714351654e-06 |
6.419990677386523e-06 |
20001 |
4.089996218681336e-06 |
8.430005982518196e-06 |
5.350005812942981e-06 |
22501 |
4.949979484081268e-06 |
9.039987344294786e-06 |
5.519995465874672e-06 |
25001 |
7.670011837035417e-06 |
9.039998985826969e-06 |
5.510030314326287e-06 |
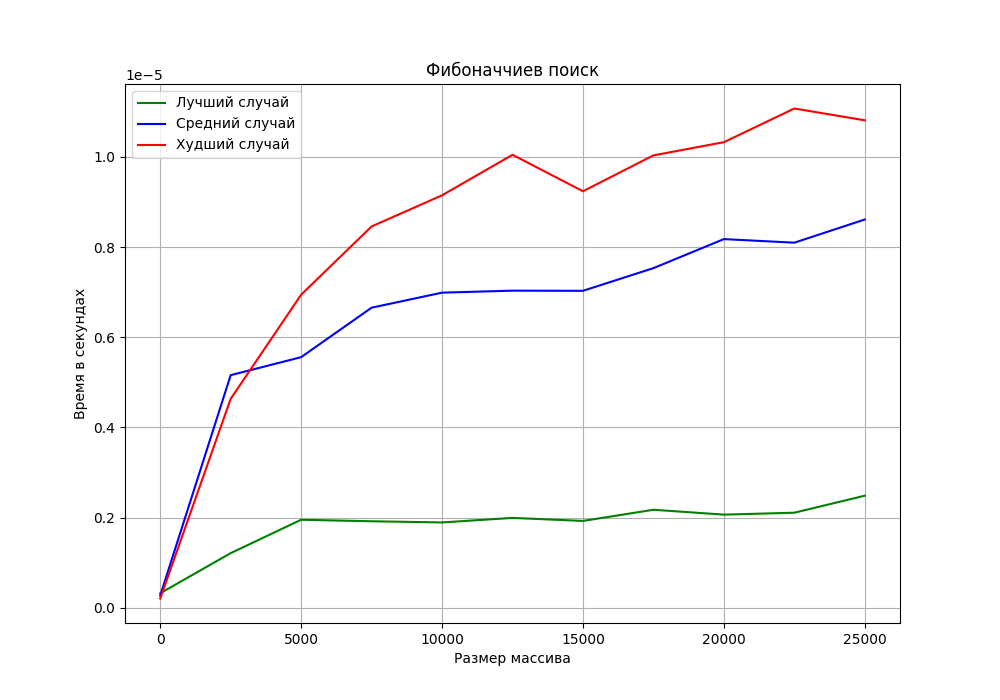
Рисунок - График временной сложности Фибоначчиева поиска с экспериментальными значениями.
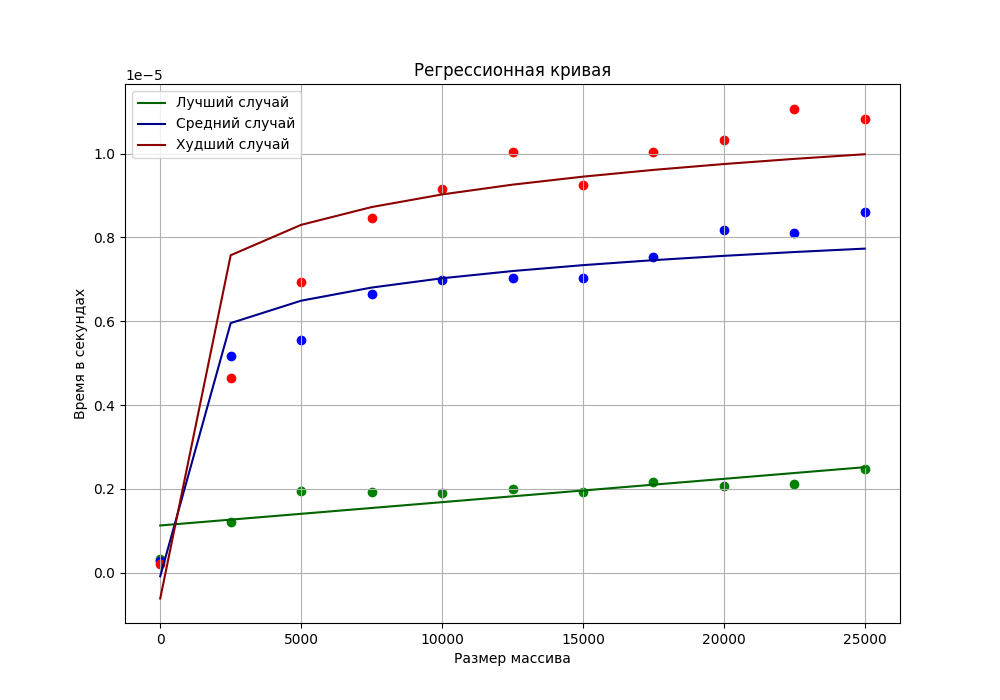
Рисунок - График экспериментальных значений с регрессионной кривой.
Таблица - Коэффициенты моделей для Фибоначчиева поиска
Случай |
Модель |
Коэффициенты |
|
|
|
||
Лучший |
=a 1+b |
|
|
Средний |
=a logn+b |
|
|
Худший |
=a*logn+b |
|
|
Сравнив график с регрессией и график из теоретической части, мы можем сделать вывод, что для среднего и худшего случаев сохраняется логарифмическая асимптотика.