
- •Аннотация
- •Введение
- •Теоретическая часть линейный поиск
- •Описание алгоритма
- •Бинарный поиск
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
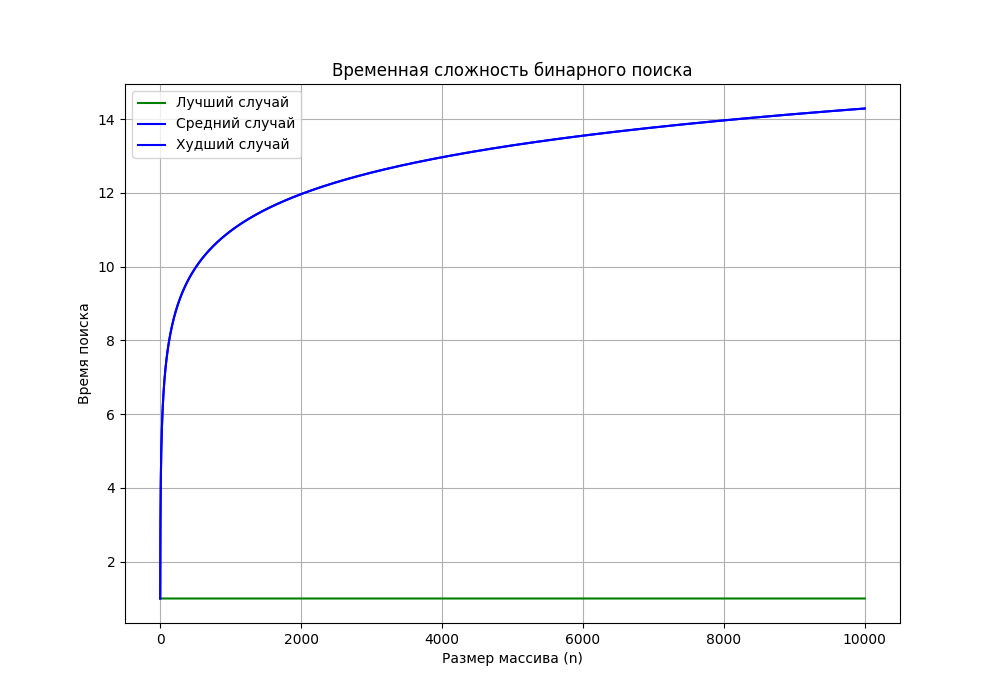
- •График функции временной сложности для всех случаев
- •Интерполяционный поиск
- •Описание алгоритма
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для всех случаев
- •Экспоненциальный поиск
- •Описание алгоритма
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для всех случаев фибоначчиев поиск (Fibonacci Search)
- •Описание алгоритма
- •Функция временной сложности и её асимптотическая оценка
- •Функция пространственной сложности и её асимптотическая оценка
- •График функции временной сложности для всех случаев
- •Сравнение временной сложности всех алгоритмов
- •Практическая часть линейный поиск
- •Бинарный поиск
- •Интерполяционный поиск
- •Экспоненциальный поиск
- •Фибоначчиев поиск
- •Сравнение временной сложности экспериментальных значений.
- •Сравнение теоретических и экспериментальных значений
- •Заключение
- •Код программы
- •Линейный поиск
- •Бинарный поиск
- •Интерполяционный поиск
- •Экспоненциальный поиск
- •Фибоначчиев поиск
Функция пространственной сложности и её асимптотическая оценка
В итеративной версии бинарного поиска:
- Не требуется выделение дополнительной памяти для рекурсии.
- Используются только несколько переменных, в данном случае, указатели на границы массива.
График функции временной сложности для всех случаев
Интерполяционный поиск
(Interpolation Search)
Интерполяционный поиск — это алгоритм, работающий с отсортированными массивами. Он улучшает бинарный поиск, предполагая, что элементы массива распределены равномерно. Вместо деления массива пополам, как в бинарном поиске, интерполяционный поиск использует значение элемента, который мы ищем, чтобы приблизительно определить, где этот элемент находится.
Описание алгоритма
Используемая формула для вычисления предполагаемого индекса:
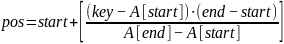
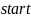 и
и
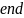 -
индексы
текущего диапазона
поиска.
-
индексы
текущего диапазона
поиска.
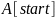 и
и
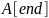 - значения элементов в начале и конце
диапазона.
- значения элементов в начале и конце
диапазона.
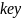 -
искомое значение.
-
искомое значение.
Алгоритм использует метод интерполяции для предсказания индекса.
Пример:
Искомое значение: 42
Массив (отсортированный):
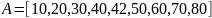
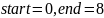
Формула для нахождения индекса:
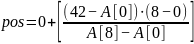
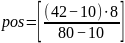
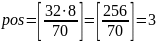
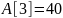
Так
как
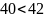 ,
,
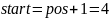
Проверяем по формуле:
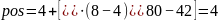

Число найдено
Функция временной сложности и её асимптотическая оценка
Лучший случай
Лучший случай наступает, если искомый элемент оказывается на предполагаемой позиции на первой итерации. Это возможно, если позиция искомого элемента равна середине массива.
Средний случай
В среднем случае интерполяционный поиск работает быстрее, чем бинарный поиск, если массив распределён равномерно.
За
один шаг алгоритм уменьшает количество
проверяемых элементов с n
до
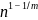 где
m
зависит
от степени равномерности массива.
То
есть, после k-ого шага количество
проверяемых элементов уменьшается до
где
m
зависит
от степени равномерности массива.
То
есть, после k-ого шага количество
проверяемых элементов уменьшается до
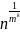 .
Завершение
поиска: интервал становится длины 1,
.
Завершение
поиска: интервал становится длины 1,
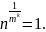
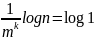
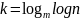
m - параметр, который определяет, насколько быстро уменьшается длина интервала на каждом шаге и зависит от степени равномерности распределения данных.
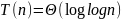
Худший случай
Если данные распределены неравномерно, интерполяционный поиск теряет свою эффективность. В крайних случаях (например, когда большинство значений одинаковы, а искомое значение сильно отличается), алгоритм может работать как линейный поиск.
В этом случае:
Функция пространственной сложности и её асимптотическая оценка
Интерполяционный поиск выполняется итеративно и не требует дополнительной памяти для хранения промежуточных структур данных или рекурсивных вызовов.
Что хранится в памяти:
Начальный и конечный индексы
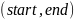 для текущего подмассива.
для текущего подмассива.Позиция вычисленного индекса поиска (
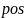 ).
).Дополнительные константные переменные для выполнения операций (например, ключ поиска и размер массива).
Таким образом, пространственная сложность интерполяционного поиска составляет:
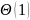
График функции временной сложности для всех случаев
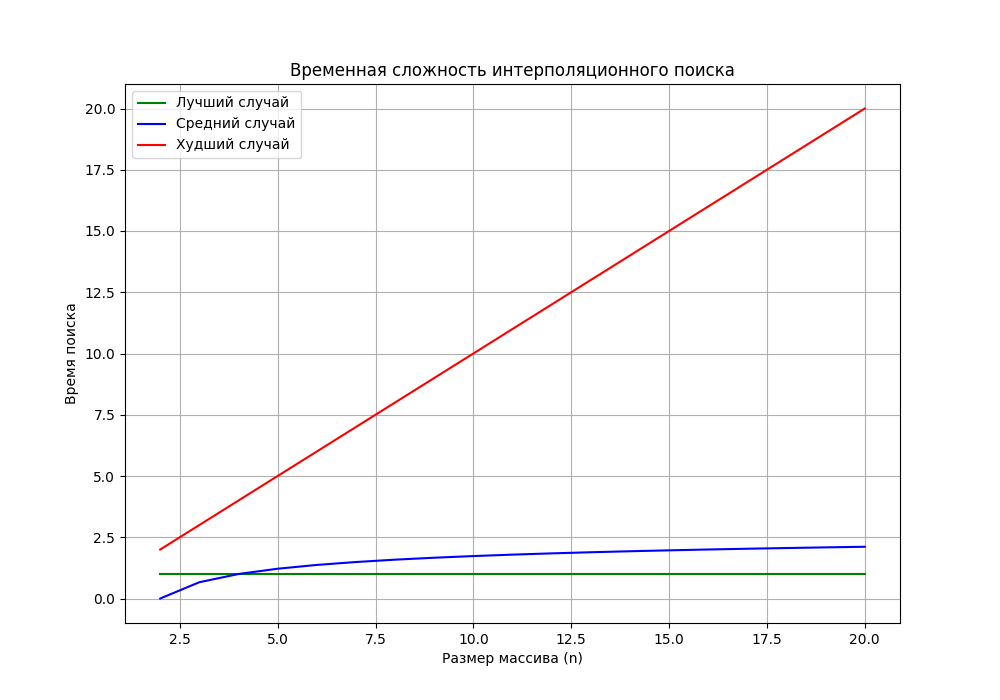
Экспоненциальный поиск
(Exponential Search)
Экспоненциальный поиск — это алгоритм поиска в отсортированном массиве. Он используется для быстрого определения диапазона, где может находиться искомый элемент. После определения диапазона выполняется бинарный поиск внутри этого диапазона.
Алгоритм начинается с поиска индекса, который экспоненциально увеличивается (1, 2, 4, 8, ...), пока не будет найден подходящий диапазон, содержащий искомый элемент.
