Красно-черное дерево

Таблица 3. - Зависимость высоты дерева поиска от количества ключей в красно-черном дереве.

Кол-во ключей	Высота
1	0
2	1
4	2
6	3
10	4
14	5
22	6
30	7
46	8
62	9
94	10
126	11
190	12
254	13
382	14
510	15
766	16

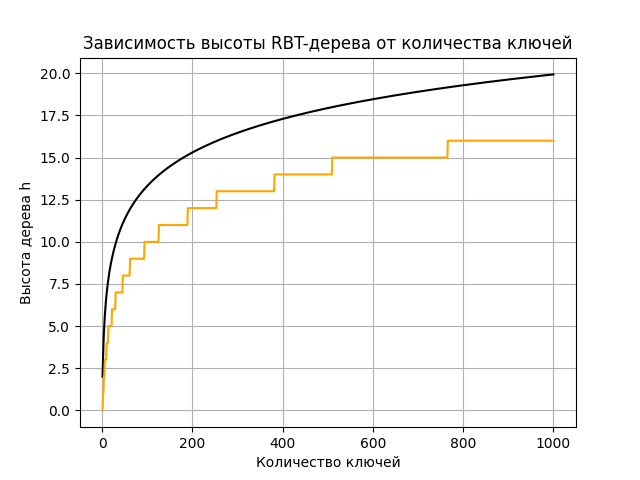
Рисунок 5 - Зависимость высоты RBT-дерева от количества ключей

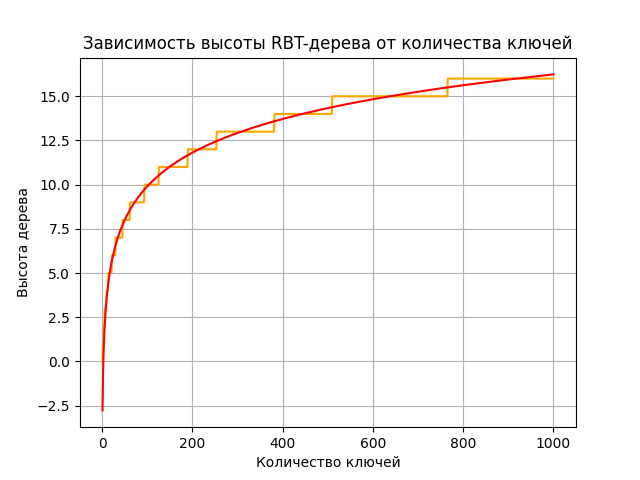
Рисунок 6 - регрессионная кривая к графику зависимости высоты RBT-дерева от количества ключей

Как и в случае АВЛ-дерева, теоретическая верхняя граница соблюдается, и график имеет логарифмическую асимптотику, но только с другим коэффициентом:

.

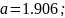
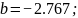
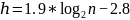Практические значения сходятся с теоретическими.

Обходы дерева

1. Обход дерева в ширину

Суть обхода двоичного дерева в ширину:

1.Корень добавляется в очередь.

2.Пока очередь не пуста, выполняется следующий процесс:

- Извлекается узел из очереди (это текущий узел для обработки);

- Обрабатывается текущий узел;

- Если у текущего узла есть дочерние узлы (левый и правый в случае дерева), они добавляются в очередь.

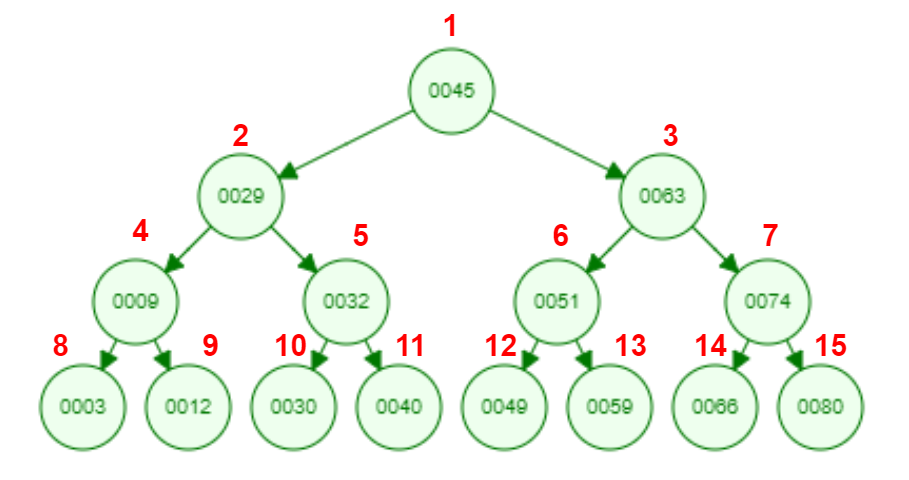
Рисунок 7 - Обход дерева в ширину наглядно.

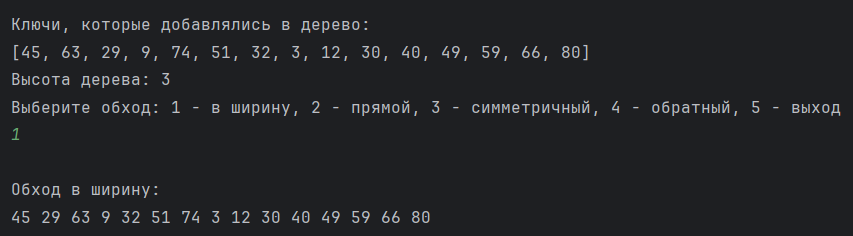
Рисунок 8 - Обход дерева в ширину.

2. Обход дерева в глубину Прямой обход или preorder

1. Проверяем, не является ли текущий узел пустым или null.

2. Показываем поле данных корня (или текущего узла).

3. Обходим левое поддерево рекурсивно, вызвав функцию прямого обхода.

4. Обходим правое поддерево рекурсивно, вызвав функцию прямого обхода.

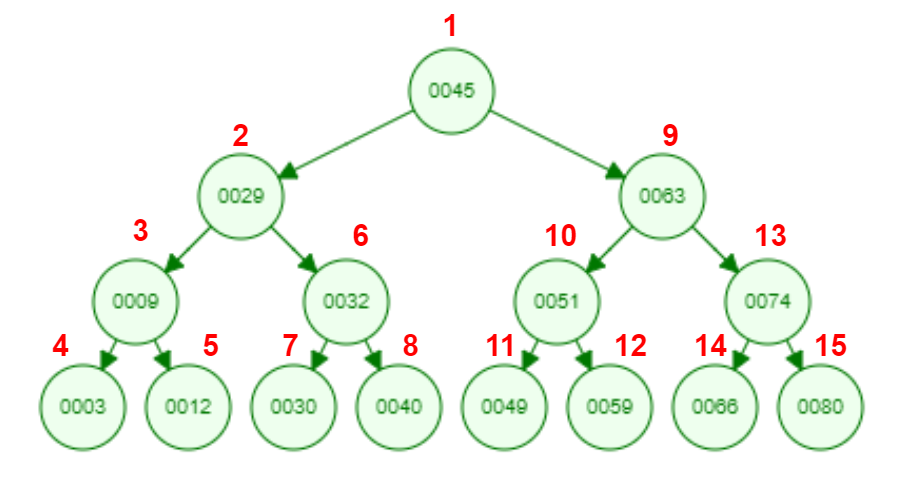
Рисунок 9 - Прямой обход наглядно.

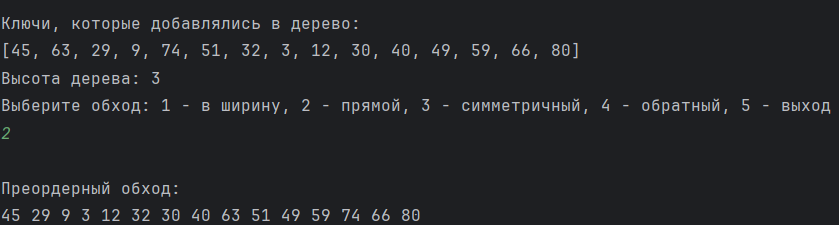
Рисунок 10 - Прямой обход.

Симметричый (центрированный) обход или inorder

1. Проверяем, не является ли текущий узел пустым или null.

2. Обходим левое поддерево рекурсивно, вызвав функцию симметричного обхода.

3. Показываем поле данных корня (или текущего узла).

4. Обходим правое поддерево рекурсивно, вызвав функцию симметричного обхода.

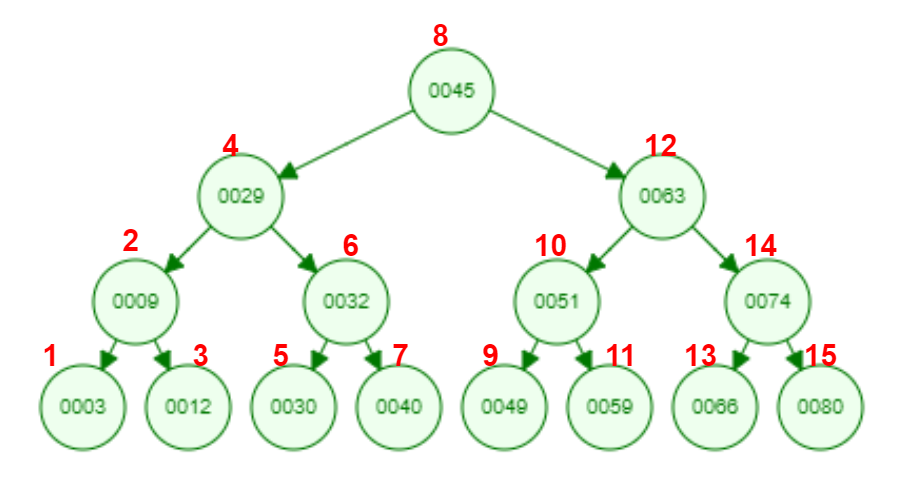
Рисунок 11 - Симметричный (центрированный) обход наглядно.

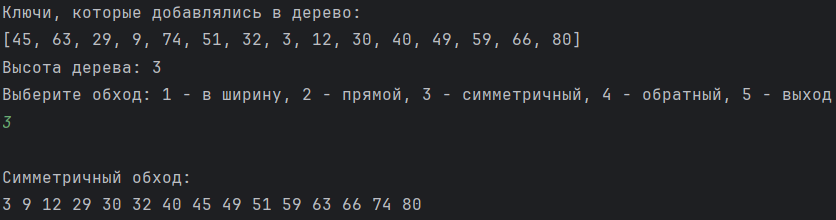
Рисунок 12 - Симметричный (центрированный) обход.

Обратный обход или postorder

1. Проверяем, не является ли текущий узел пустым или null.

2. Обходим левое поддерево рекурсивно, вызвав функцию обратного обхода.

3. Обходим правое поддерево рекурсивно, вызвав функцию обратного обхода.

4. Показываем поле данных корня (или текущего узла).

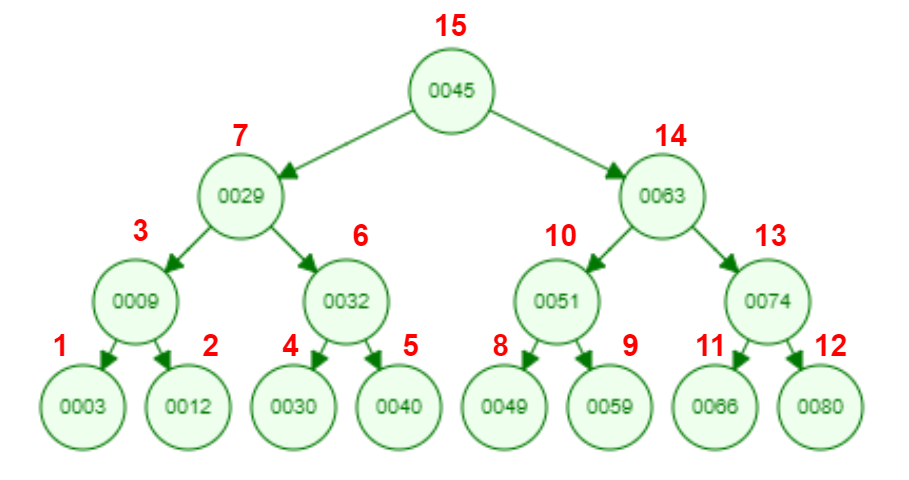
Рисунок 13 - Обратный обход наглядно.

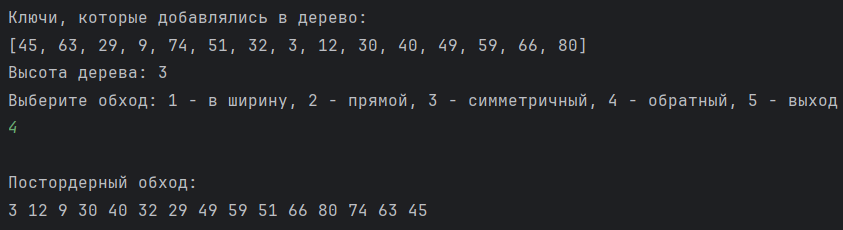
Рисунок 14 - Обратный обход.

Ссылка на гугл коллаб:

https://colab.research.google.com/drive/1gBvfNeVjRfbgABJcK-_3-CuM4iI9HQMV?usp=sharing