Верхняя оценка высоты красно-черного дерева

Красно-черное дерево — менее строго сбалансированное, чем АВЛ-дерево, но также поддерживает логарифмическую высоту.

Свойства:

1. Максимальная высота достигается, если все узлы на пути от корня к листу черные, кроме одной стороны, где чередуются красные и черные узлы.

2. Минимальная высота (чисто черное дерево):

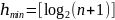
3. Максимальная высота достигается, если каждое черное ребро сопровождается красным, т.е. для каждого черного узла может быть красный узел.

Чёрные узлы и высота:

В красно-черном дереве с черной высотой bh количество внутренних вершин равно  .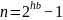

Рассмотрим красно-чёрное дерево с высотой h. Так как у красной вершины чёрные сыновья, количество красных вершин не больше 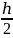 . Тогда чёрных вершин не меньше, чем  .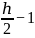

Тогда по лемме, для количества внутренних вершин в дереве выполняется неравенство:

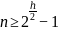
Преобразовав данное неравенство, мы получим верхнюю оценку высоты красно-черного дерева:

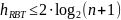
Практическая часть Асимптотика Бинарное дерево поиска (bst)

1. Лучший случай:

Описание: При добавлении узлов дерево оказывается сбалансированным (разница высоты между поддеревьями каждого узла не превышает 1). Это характерно для сбалансированных деревьев, например, AVL или красно-черных деревьев, но возможно и в BST при удачном порядке вставки.

Высота: Для идеально сбалансированного BST с n узлами высота ℎ будет:

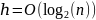
2. Средний случай:

Описание: Если порядок вставки элементов случайный, высота BST будет варьироваться, но при большом n в среднем она приближается к:

3. Худший случай:

Описание: В худшем случае элементы вставляются в отсортированном порядке (в возрастающем или убывающем), и каждое добавление нового элемента создает новый уровень. В итоге дерево превращается в список.

Высота: Для n узлов высота ℎ равна:

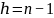
Итог:

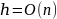
Зависимость высоты дерева от количества ключей Бинарное дерево поиска

Таблица 1. - Зависимость высоты дерева поиска от количества ключей в бинарном дереве поиска.

Кол-во ключей	Высота
1	0
2	1
3	2
7	3
8	4
13	5
16	6
36	7
37	8
39	9
51	10
77	11
109	12
148	13
169	14
219	15
289	16
294	17
438	18
711	19
834	20

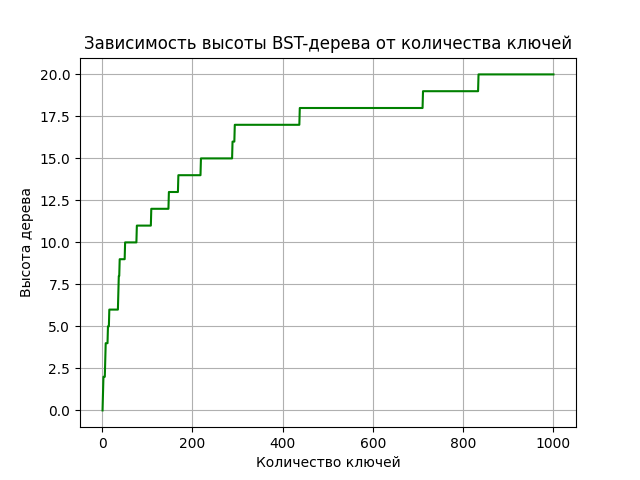
Рисунок 1 - Зависимость высоты BST-дерева от количества ключей

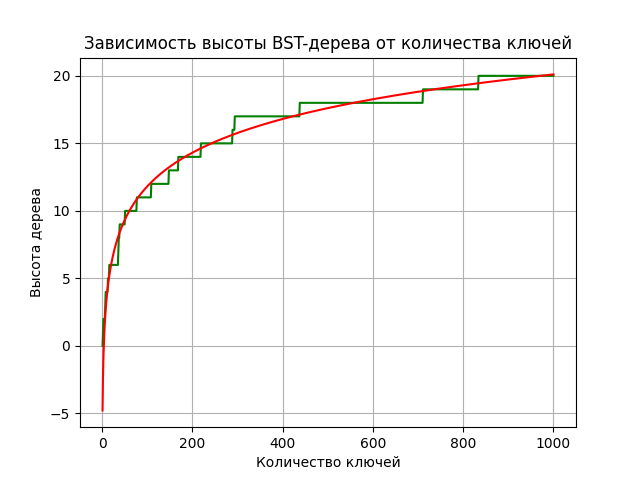
Рисунок 2 - регрессионная кривая к графику зависимости высоты BST-дерева от количества ключей

По рисунку можно предположить, что график имеет асимптотику, схожую с логарифмической. Если построить график вида , то можно заметить, что он достаточно близко ложиться к нашим данным.

Коэффициенты кривой:

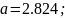
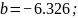
Итог:

.

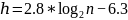АВЛ-дерево

Таблица 2. - Зависимость высоты дерева поиска от количества ключей в АВЛ-дереве.

Кол-во ключей	Высота
1	0
2	1
3	2
5	3
9	4
17	5
33	6
65	7
129	8
257	9

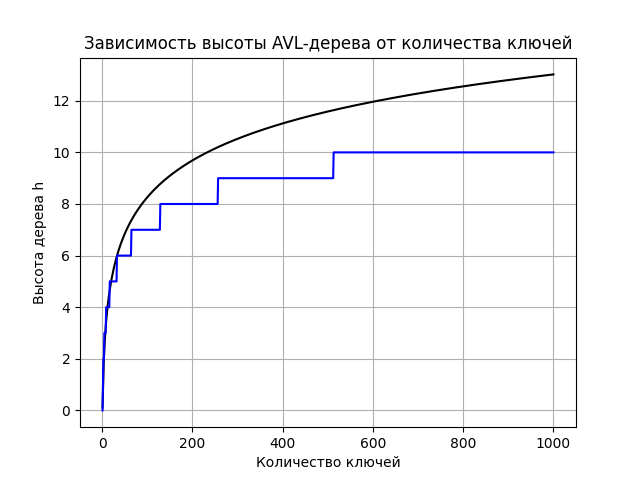
Рисунок 3 - Зависимость высоты AVL-дерева от количества ключей

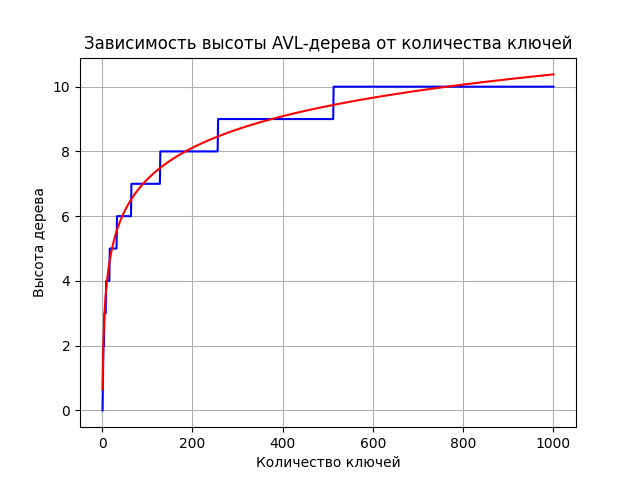
Рисунок 4 - регрессионная кривая к графику зависимости высоты AVL-дерева от количества ключей

Смотря на график зависимости высоты дерева от его количества элементов видно, что верхняя граница высоты соблюдается, можно предположительно сказать, что это похоже на теоретические значения, поскольку каждый следующий отрезок графика длиннее предыдущего, что характерно для графика логарифма.

Если построить график вида , то можно заметить, что он достаточно близко ложиться к нашим данным.

Коэффициенты кривой:

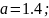
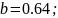
Итог:

.

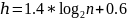Можно сделать вывод, что практические значения сходятся с теоретическими.