МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра САПР

отчет

по лабораторной работе №2

по дисциплине «Алгоритмы и структуры данных»

Тема: Самобалансирующиеся двоичные деревья поиска

Студентка гр. 3352
Преподаватель

Санкт-Петербург

2024

Цель работы: реализация самобалансирующихся деревьев поиска и экспериментальная проверка оценок высоты данных деревьев.

Задачи для теоретической части:

1. Дать определение АВЛ дерева. Кратко описать алгоритм вставки/удаления с последующей балансировкой для АВЛ-дерева. Получить верхнюю оценку высоты АВЛ-дерева.

2. Дать определение красно-черного дерева. Кратко описать алгоритм вставки/удаления с последующей балансировкой для красно-черного дерева.-дерева. Получить верхнюю оценку высоты красно-черного дерева.

Задачи для практической части:

1. Реализовать бинарное дерево поиска, красно-черное дерево и АВЛ дерево (структура, балансировка, операции вставки/удаления/поиска).

2. Получить зависимость высоты дерева поиска от количества ключей, при условии, что значение ключа - случайная величина, распределенная равномерно. Определить, какая асимпотика функции h(n) наблюдается у двоичного дерева поиска.

3. Получить зависимость высоты АВЛ и красно-черного дерева поиска от количества ключей, при условии, что значения ключей монотонно возрастают.

4. Вывести полученные результаты на графики

5. Сравнить с теоретической оценкой высоты.

6. Реализовать обходы в глубину и обход в ширину двоичного дерева с выводом результата.

Теоретическая часть

АВЛ-дерево (AVL Tree)

АВЛ-дерево — это самобалансирующееся двоичное дерево поиска, в котором для каждой вершины выполняется условие балансировки: разница высот левого и правого поддеревьев не превышает 1.

Основные операции с авл-деревом

1. Вставка:

Допустим, в дерево нужно вставить узел 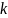. У нас есть 3 случа вставки нового узла:

1. Если меньше текущего узла, нужно перейти в левое поддерево.

2. Если больше текущего узла, нужно перейти в правое поддерево.

3. Если достигается пустое место (NULL), создаём новый узел и вставляем значение .

2. Удаление

Удаление узла из АВЛ-дерева выполняется по стандартным правилам для двоичного дерева поиска:

1. Удаляемый узел — лист (не имеет потомков): просто удаляем узел.

2. Удаляемый узел имеет одного потомка: заменяем удаляемый узел его единственным потомком.

3. Удаляемый узел имеет двух потомков:

   1. Находим наименьший узел в правом поддереве (преемник) или наибольший узел в левом поддереве (предшественник).

   2. Копируем его значение в удаляемый узел.

   3. Рекурсивно удаляем найденный узел (который будет либо листом, либо иметь одного потомка).

Обновление высоты:

После вставки или удаления обновляем высоты всех узлов на пути от добавленного узла к корню:

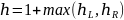
Проверка баланс-фактора:

Для каждого узла на пути к корню вычисляем его баланс-фактор:

.

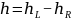Если баланс-фактор выходит за пределы диапазона [−1,1], выполняется балансировка.

3. Балансировка после вставки/удаления:

Правое вращение (Right Rotation): для левостороннего дисбаланса (левый-левый случай).

Левое вращение (Left Rotation): для правостороннего дисбаланса (правый-правый случай).

Лево-правое вращение (Left-Right Rotation): для левостороннего дисбаланса (левый-правый случай).

Право-левое вращение (Right-Left Rotation): для правостороннего дисбаланса (правый-левый случай).

Верхняя оценка высоты авл-дерева

АВЛ-дерево — это строго сбалансированное двоичное дерево поиска, где разница высот левого и правого поддерева любого узла не превышает 1.

Связь между числом узлов 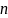и высотой :

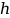Мы знаем, что минимальное число узлов в АВЛ-дереве с высотой h имеет вид:

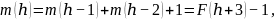
где 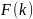– k-ое число Фибоначчи

Число Фибоначчи:

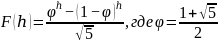
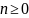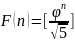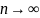Из формулы Бине следует, что для всех число . В частности, при справедлива асимптотика .

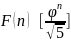Фактическое количество узлов n в дереве может быть больше минимального количества m, поэтому справедливо неравенство:

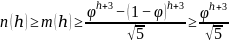
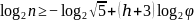
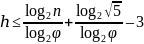
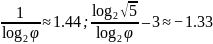
Следовательно, высота ограничена сверху выражением:

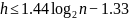
Красно-черное дерево (rb Tree)

Красно-черное дерево — это самобалансирующееся двоичное дерево поиска, в котором соблюдаются следующие свойства:

1. Каждый узел либо красный, либо черный.

2. Корень дерева — черный.

3. У всех листовых (пустых) узлов цвет черный.

4. Если узел красный, оба его потомка — черные (нет двух подряд красных узлов).

5. На любом пути от корня к листу одинаковое количество черных узлов. Это называется черной высотой.

Основные операции с красно-черным деревом

1. Вставка

Как и для АВЛ-дерева, у нас есть 3 случа вставки нового узла:

1. Если меньше текущего узла, нужно перейти в левое поддерево.

4. Если больше текущего узла, нужно перейти в правое поддерево.

5. Если достигается пустое место (NULL), создаём новый узел и вставляем значение .

Новый узел всегда окрашивается в красный. Если дерево пустое, новый узел становится черным корнем.

Проверка свойств дерева:

1. Если родитель нового узла черный, свойства красно-черного дерева сохраняются. Вставка завершена.

2. Если родитель красный, возможно нарушение свойств. Выполняется балансировка.