
Лаб. №4
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Информатика»
Лабораторная работа №4
«Моделирование простейших логических схем»
по дисциплине:
«Математическая логика и теория алгоритмов»
Вариант №8
Проверил: Сёмин В.Г.
Москва 2023
Таблица истинности для задания определяется датой дня рождения студента. Для этого необходимо дату представить в формате ДД:ММ:Гг. Десятилетие Г исключается (просто откидывается). В результате получаем ДДММг. Полученное число нужно перевести в двоичный формат представления данных. Результат необходимо дополнить до 16 разрядов дописав перед числом необходимое количество нулей.
Дата: 28.05.05. Отбрасываем «0», получаем 28055. Переводим в двоичную систему счисления:
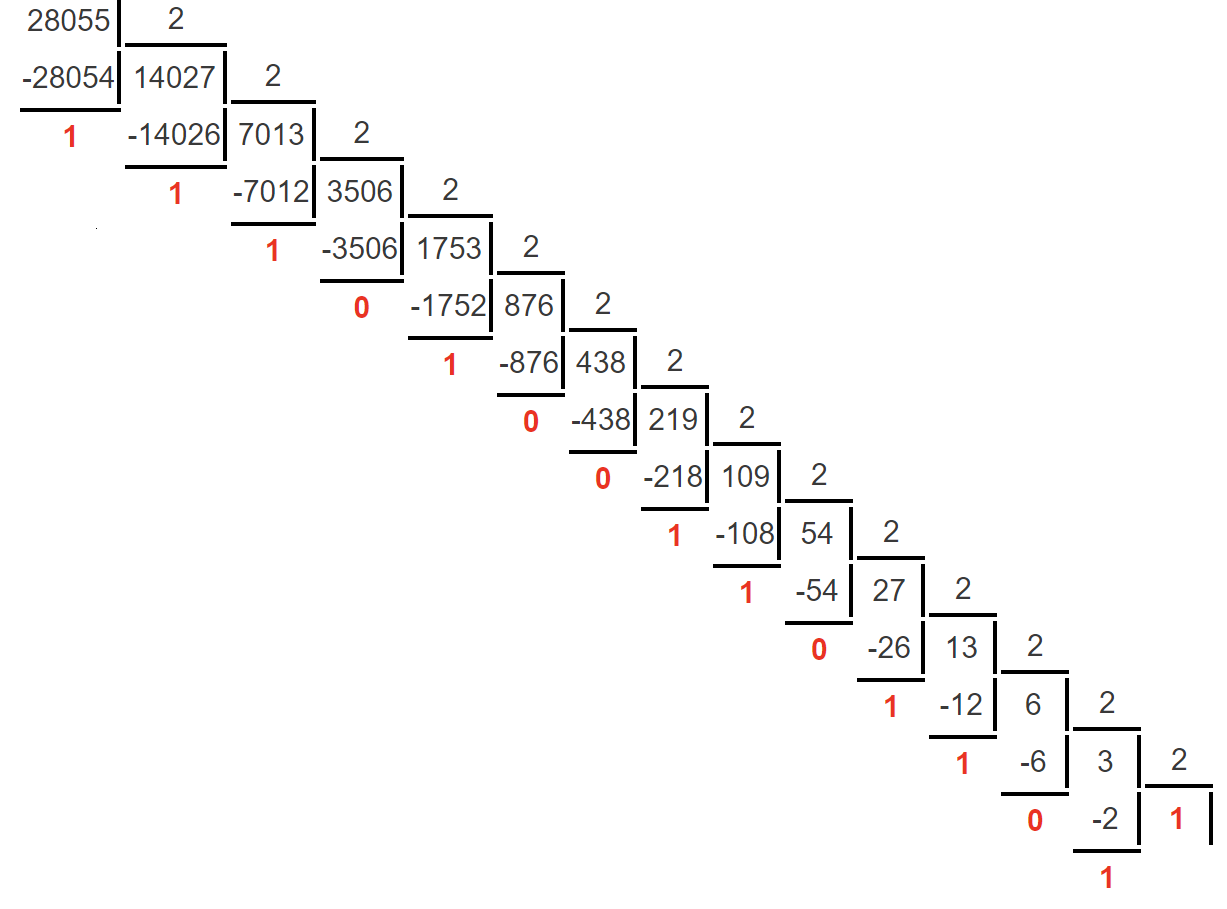 Результат
- 110 1101 1001 0111. Дополняем до 16-ти разрядов
нулями в старших порядках. В итоге
получаем
0110 1101 1001 0111 - результирующая логическая
функция.
По ней составим таблицу истинности.
Результат
- 110 1101 1001 0111. Дополняем до 16-ти разрядов
нулями в старших порядках. В итоге
получаем
0110 1101 1001 0111 - результирующая логическая
функция.
По ней составим таблицу истинности.
Сформированный вариант задания:
x3 |
x2 |
x1 |
x0 |
f |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Задание 1. Реализовать полученную функцию на логических элементах.
В результирующей логической функции количество единиц больше, чем нулей (нулей - 6, единиц - 10). Поэтому рационально использовать совершенную конъюнктивную нормальную форму (СКНФ).
f(x3, x2, x1, x0) = (x3 + x +
x1 + x0) * (x3
+ x2 +
+
x1 + x0) * (x3
+ x2 +
 +
+
 )
* (x3
+
)
* (x3
+
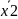 +
+
x0)*
+
+
x0)*
* ( + x2
+ x1 +
)
* (
+ x2
+
+
x0) * (
+
+
x1 + x0)
+ x2
+ x1 +
)
* (
+ x2
+
+
x0) * (
+
+
x1 + x0)
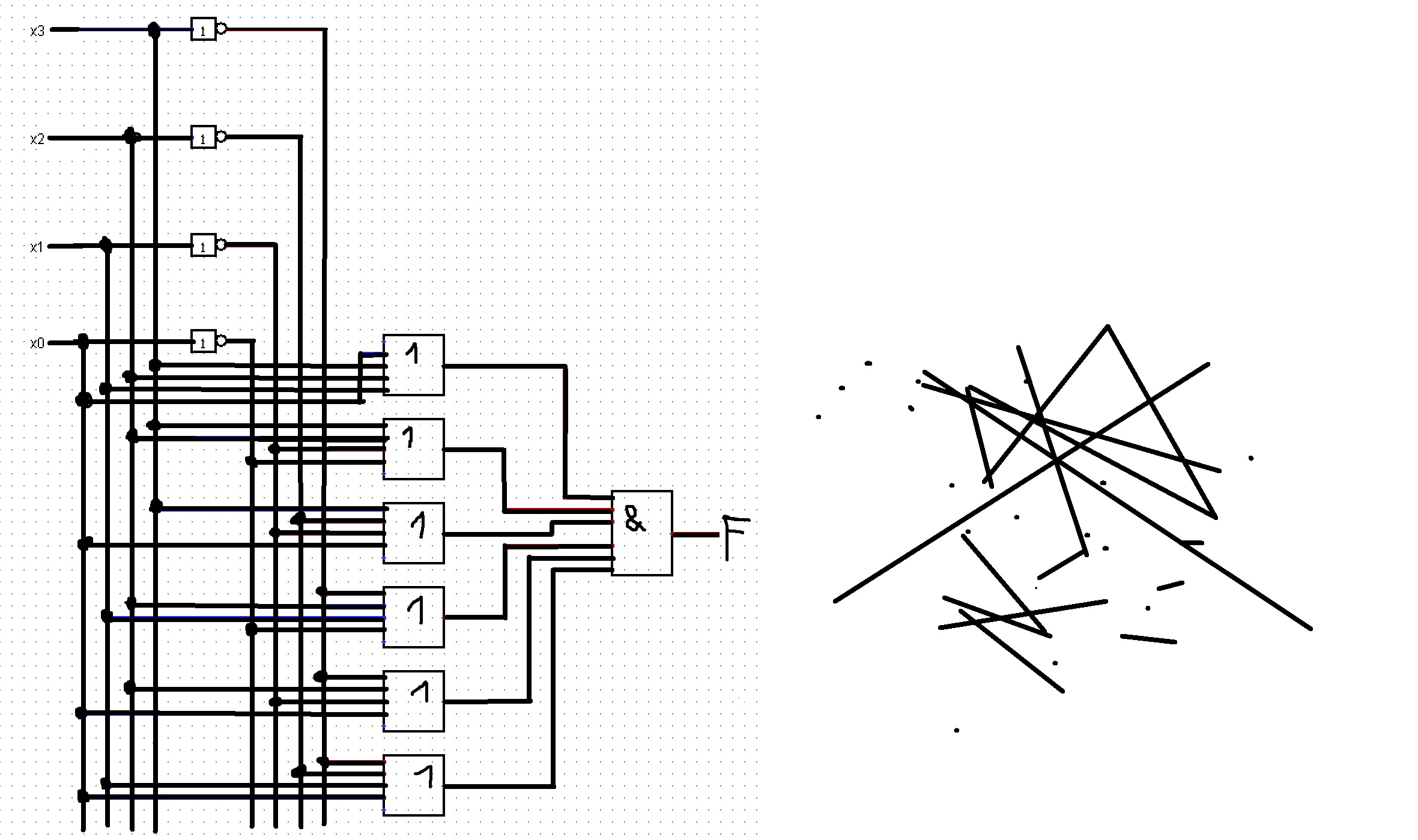
Схема реализации функции на логических элементах
Задание 2. Выполнить минимизацию по карте Карно, синтезировать схему на
базисе, определенного вариантом, привести синтезируемую схему,
выполнить проверку на соответствие исходной таблице истинности.
Составление карты Карно.
x1x0
x3x2 |
00 |
01 |
11 |
10 |
00 |
0 |
1 |
0 |
1 |
01 |
1 |
1 |
1 |
0 |
11 |
0 |
1 |
1 |
1 |
10 |
1 |
0 |
1 |
0 |
Операция склеивания «0» (процесс склеивания клеток в группы).
x1x0
x3x2 |
00 |
01 |
11 |
10 |
00 |
|
1 |
|
1 |
01 |
1 |
1 |
1 |
|
11 |
|
1 |
1 |
1 |
10 |
1 |
|
1 |
|
Процесс склеивания использует правила №1, №3.
Считывание функции.
Так как m = 0, значит, КНФ является уже минимизированной, следовательно:
F = (x3 + x2 + x1 + x0) * (x3 + x2 + + ) * (x3 + + + x0) * ( + x2 + x1 + ) * ( + x2 + + x0) * ( + + x1 + x0) - МКНФ
Переходим в базис ИЛИ-НЕ с помощью законов де Моргана:
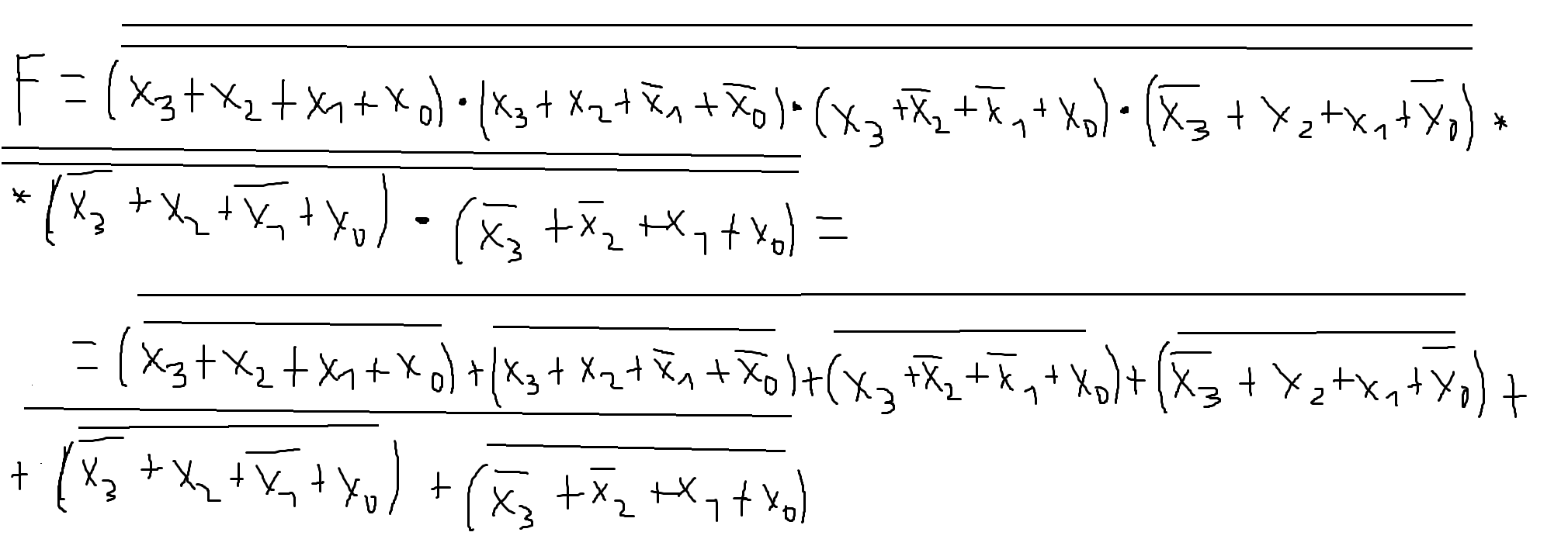
Построим схему по полученному выражению:
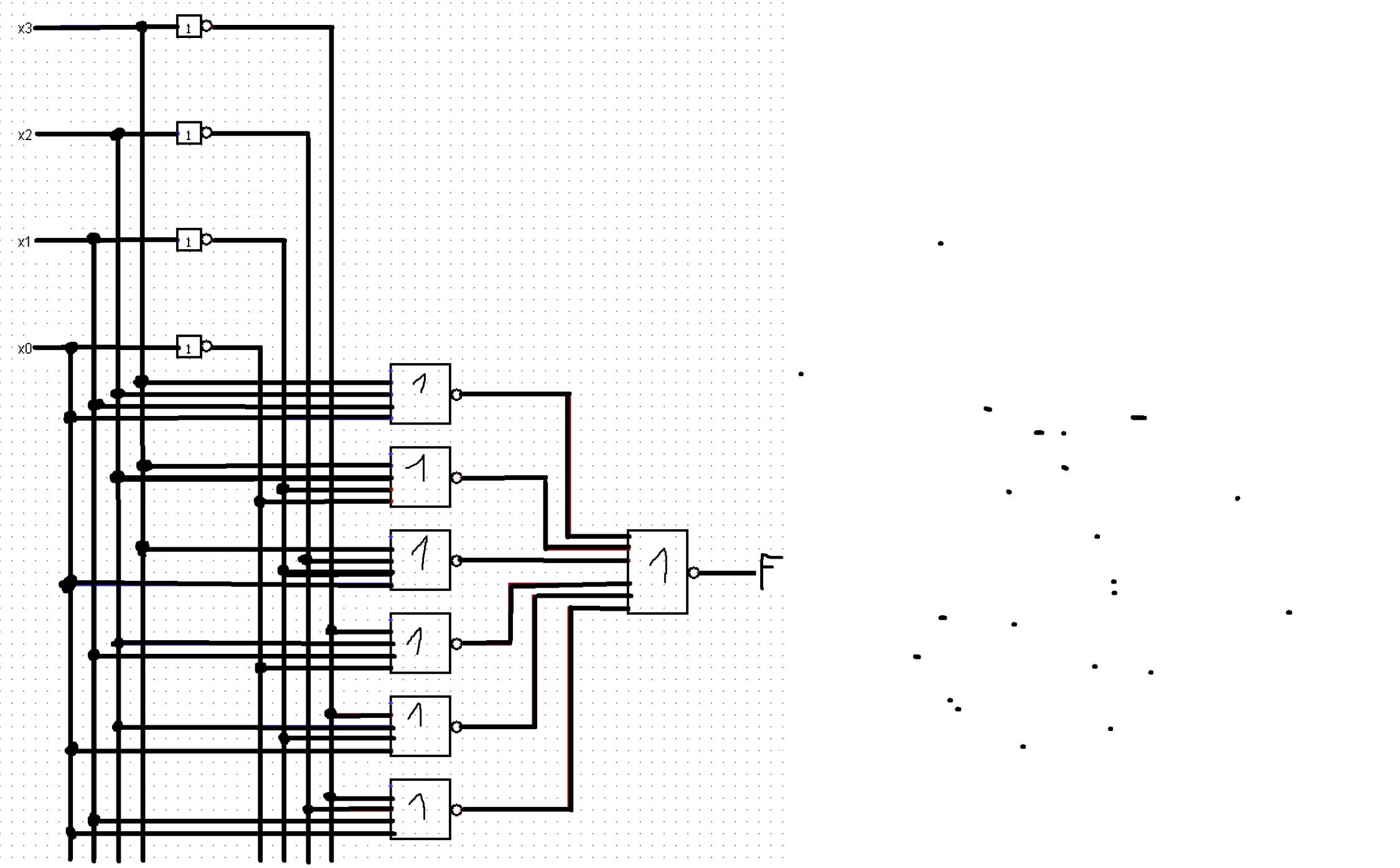
Построим таблицу истинности для функции в базисе ИЛИ-НЕ:
x3 |
x2 |
x1 |
x0 |
F |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Видно, что результаты данной таблицы соответствуют результатам таблицы исходной функции, следовательно, функция была правильна синтезирована на базисе ИЛИ-НЕ.






