Экзамен

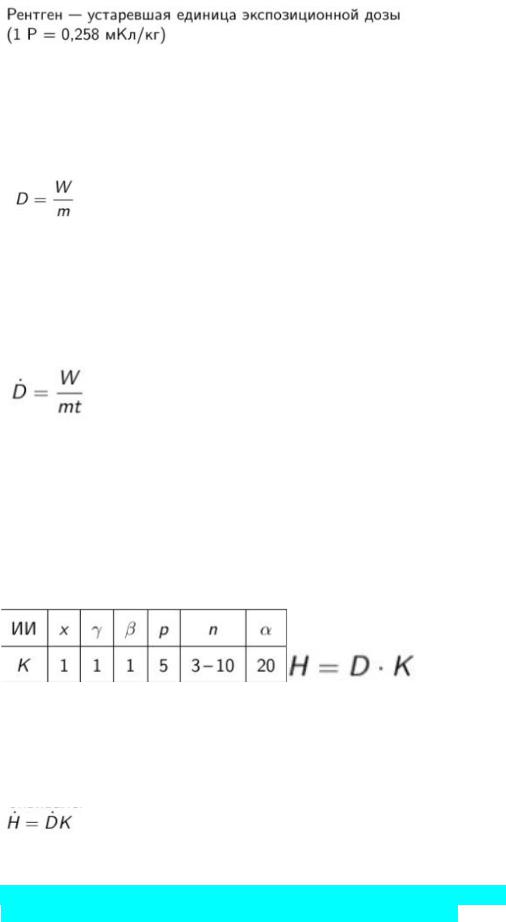
Поглощённая доза

Поглощённая доза — величина энергии W ионизирующего излучения, переданная веществу массы m:

Единица измерения в СИ — грей (1 Гр = 1 Дж/кг)

Недостаток — не отражает биологический эффект облучения.

Мощность поглощённой дозы — доза, поглощаемая в единицу времени:

Единица измерения в СИ — грей в секунду (1 Гр/с = 1 Вт/кг)

Эквивалентная доза

Эквивалентная доза H характеризует биологический эффект облучения организма ионизирующим излучением. Коэффициент качества K ионизирующего излучения — величина, которая показывает во сколько раз данное ионизирующее излучение сильнее повреждает ткани организма по сравнению с гамма-излучением.

Единица измерения — зиверт (Зв)

Мощность эквивалентной дозы — эквивалентная доза, поглощаемая в единицу времени:

16. Гипотеза де Бройля. Волновая природа микрочастиц. Опыт ДэвиссонаДжермера. Корпускулярно-волновой дуализм.

Корпускулярно-волновой дуализм

Корпускулярные свойства:

1. Излучение абсолютно чёрных тел, равновесное тепловое излучение

-гипотеза Планка о существовании квантов энергии

2.Фотоэффект

3.Эффект Комптона – фотоны

4.Давление света

Волновые свойства:

1.Интерференция

2.Дифракция

3.Дисперсия

4.Поляризация

Принцип дополнительности Бора: для полного описания квантовомеханических явлений необходимо применять два взаимоисключающих набора классических понятий, совокупность которых даёт исчерпывающую информацию об этих явлениях как о целостных.

В 1924 г. Луи де Бройль (французский физик) пришел к выводу, что двойственность света должна быть распространена и на электроны. Гипотеза де Бройля заключалась в том, что электрон, корпускулярные свойства которого (энергия E и импульс p) изучаются давно, имеет еще и волновые свойства (частота v и длина волны λ), т.е. при определенных условиях ведет себя как волна.

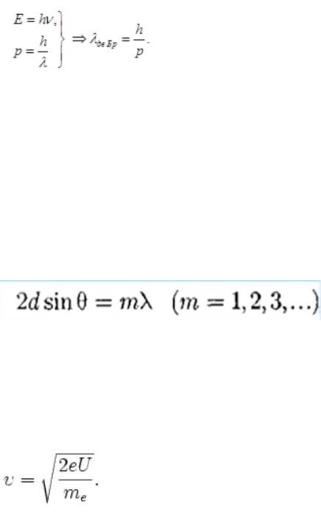
Идея де Бройля состояла в том, что это соотношение имеет универсальный характер, справедливый для любых волновых процессов. Любой частице, обладающей импульсом р, соответствует волна, длина которой вычисляется по формуле де Бройля.

Опыт Дэвиссона и Джермера

Гипотеза: если электрон обладает волновыми свойствами, то дифракционный максимум должен наблюдаться при выполнении условия Вульфа-Брэгга:

Установка: установка включала в себя монокристалл никеля, сошлифованный под углом, и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением U на электронной пушке:

Коллектор (детектор), соединённый с чувствительным гальванометром, можно устанавливать под любым углом относительно падающего луча. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме. В опытах измерялась интенсивность

рассеянного кристаллом электронного пучка в зависимости от угла рассеяния 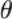и от скорости электронов в пучке (разности потенциалов).

Результаты:

Первый дифракционный максимум наблюдался под углом = 50о. Импульс электрона связан с его кинетической энергией формулой

Из формулы де Бройля определяем длину волны электронов:

В то же время по формуле Брэгга-Вульфа для максимума первого порядка при дифракции на кристалле никеля с периодом решетки d = 0,091 нм получаем:

Оба результата хорошо совпадают, что подтверждает наличие волновых свойств у электронов.

Электроны в теории Бора движутся по круговым орбитам. Де Бройль им соответствует круговые стоячие волны, которые «замыкаются» на себя. Если длина волны такова, что не позволяет волне «замкнуться», то на круговой орбите происходит ослабляющая интерференция, и волна быстро затухает. Следовательно,

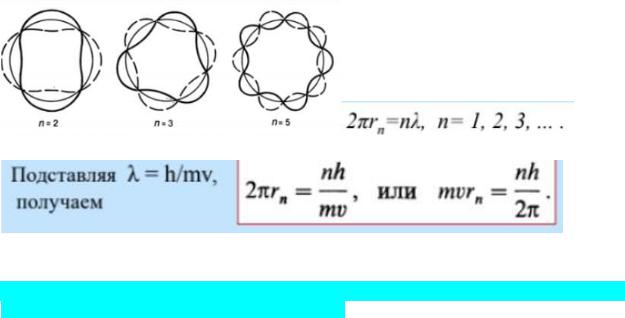
возможны только те волны, у которых на круговой орбите укладывается целое число длин волн.

17. Физические основы квантовой механики. Принцип соответствия. Принцип причинности. Принцип дополнительности.

Классическая механика, которая была выведена из наблюдений над большими телами и в которой о волновых свойствах тел даже не подозревали, прекрасно удовлетворяет задачам, возникающим при исследовании движения небесных светил, частей механизмов и т.д. Но именно поэтому классическая механика совершенно непригодна для трактовки атомных явлений. Для решения задач этого типа нельзя ограничиться механикой Ньютона, и необходимо разработать совершенно новую механику, которая учитывала бы волновые свойства вещества.

Дополнение: квантовая механика не противоречит классической механике Ньютона. Когда скорости частиц сопоставимы со скоростью света применяют теорию относительности, которая в случае малых скоростей переходит в Ньютоновскую механику (как и квантовая механика при несущественной роли волновых свойств частиц). Если же рассматривается явление, в котором существенны и волновые свойства и скорости велики, применяют квантовую механику и теорию относительности вместе - релятивистскую квантовую механику.

Принцип соответствия: классическую механику следует считать предельным случаем квантовой механики при определённых условиях (квантовая механика при её применении к макроскопическим явлениям должна приводить к законам классической механики).

Принцип причинности

Принцип дополнительности: для полного описания квантовомеханических явлений необходимо применять два взаимоисключающих набора классических понятий, совокупность которых даёт исчерпывающую информацию об этих явлениях как о целостных.

18. Принцип неопределенности Гейзенберга. Неопределенность координат и времени.

Неопределенность энергии и импульса.

Двойственная корпускулярно-волновая природа микрочастиц определяет ещё одно необычное, с точки зрения классических представлений, свойство микрообъектов – невозможно одновременно точно определить координату и ипульс частицы. В общем случае это свойство микрообъектов называется соотношением неопределённостей Гейзенберга: микрочастица не может иметь одновременно определённую координату (x,y,z) и определённую соответствующую проекцию момента имплульса (px,py,pz), причём неопределённости этих величин удовлетворяют соотношениям:

т.е. произведение неопределённостей координаты и соответствующей ей проекций импульса не может быть меньше величины порядка h.

Рассмотрим движение частицы вдоль оси Y, на пути которой установлено препятствие с небольшим отверстием. До прохождения через отверстие частица имеет вполне определенное значение проекции импульса на ось х, так как по условию задачи известно, что перемещение частицы происходит в заданном направлении.

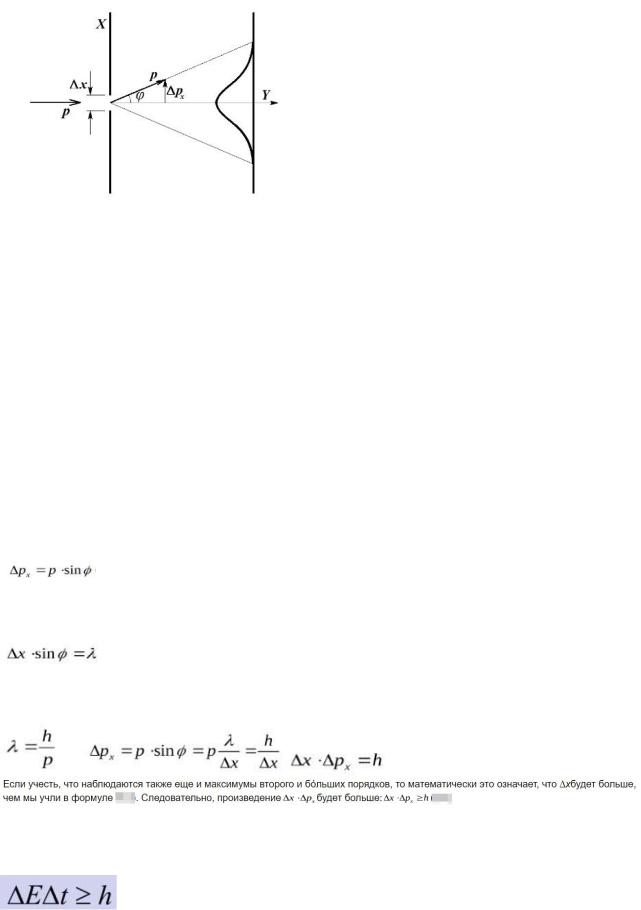
Однако при этом мы совершенно не знаем, в какой точке находится частица в каждый момент времени. Знаем, куда движется, не знаем, где находится, и наоборот! То есть для частицы квантовой природы утрачивает смысл понятие траектория.

В тот момент, когда частица проходит через отверстие, мы можем указать для нее довольно точное местоположение – ее координата попадет в интервал ∆x, равный ширине отверстия. В тот же самый момент происходит изменение импульса частицы. Его значение становится неопределенным ровно на столько, на сколько определенным стало значение координаты частицы.

То есть мы получаем некоторый разброс в направлении движения частицы после прохождения преграды, что и отражается в виде появления ненулевого ∆px. Как показывают эксперименты, вследствие дифракции, частица может вылететь в любом направлении в пределах угла 2φ (рассматриваем центральный дифракционный максимум, так как при дифракции на одной щели интенсивность остальных максимумов пренебрежимо мала). Как видно из рисунка частица, прошедшая под углом φ, имеет неопределенность импульса ∆px:

Для первого дифракционного максимума выполняется соотношение:

Учтем, что длина волны де Бройля может быть записана через импульс:

Аалогичное соотношение можно записать для другой пары физических величин – энергии и времени:

19. Уравнение Шредингера. Волновая функция и ее статистический смысл.

Для описания движущихся микрочастиц в квантовой теории разработан некий математический формализм, суть которого в следующем. Каждой микрочастице ставится в соответствие некоторая функция, значение которой зависит от координат и времени – это так называемая пси-функция. Формально пси-функция обладает своством классической волны, поэтому её часто называют волновой функцией. Волновая функция является основным носителем информации о волновых и квантовых свойствах частицы и полностью описывает их состояние.

Квадрат модуля волновой функции пропорционален вероятности обнаружить частицу в момент времени t в элементе объёма dV = dx*dy*dz:

Волновая функция удовлетворяет условию нормировки:

т.е. обнаружить частицу в бесконечном объёме есть достоверное событие.

Согласно опытным данным, параллельный пучок микрочастиц обладает свойствами плоской волны, распространяющейся в направлении движения частиц со скоростью V. Уравнение плоской волны в общем виде:

Чтобы это уравнение описывало процесс распространения волн де Бройля (движение микрочастиц), необходимо ввести в него характеристики частицы:

r = x

Основным уравнением квантовой механики является уравнение Шредингера. Состояние микрочастиц в квантовой механике описывается волновой функцией или Ψ (пси)-функцией. Эта функция является функцией координат и времени и может быть найдена путем решения уравнения ((общее нестационарное уравнение Шредингера):

Уравнение Шредингера, как и уравнение Ньютона в классической механике, не может быть получено теоретически, а представляет собой обобщение большого числа опытных фактов. Справедливость этого соотношения доказывается тем, что все вытекающие из него следствия самым точным образом согласуются с опытными фактами.

Из уравнения Шредингера следует, что вид волновой функции Ψ определяется потенциальной энергией U, т.е. характером тех сил, которые действуют на частицу. В общем виде потенциальная энергия U есть функция координат и времени. Для стационарного (не меняющегося во времени) силового поля потенциальная энергия U явно от времени не зависит. В этом случае волновая функция Ψ распадается на два множителя, один из которых зависит только от времени, второй – только от координат.

Подставляя эту функцию в уравнение Шредингера, получим:

Это уравнение Шредингера для стационарных состояний. Оба уравнения справедливы для любой частицы, движущейся с малой (V«c) скоростью. Кроме того, на волновую функцию накладываются дополнительные условия:

20. Потенциальный порог (потенциальная ступень). Прохождение частицей потенциального барьера конечной высоты. Туннельный эффект. Потенциальный порог

Пусть слева на порог налетает частица с полной энергией Е. На языке квантовой теории это означает, что на порог слева «падает» дебройлевская волна.

Низкий потенциальный порог (E>U0)