ИРС_7

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение

высшего образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Инженерная школа новых производственных технологий

Обеспечивающее подразделение: Отделение материаловедения

Направление подготовки: 12.03.02 Оптотехника

ООП: Оптико-электронные приборы и системы

ИНДИВИДУАЛЬНАЯ РАБОТА СТУДЕНТА №7

дисциплина "Физические основы источников излучения"

Вариант 4

Выполнил:

студент группы 4В11 _________________

Проверил:

доктор ф-м.н., профессор ОМ ИШНПТ _________________ В.Ф. Штанько

Томск - 2023

Исходные данные:

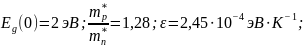
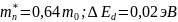
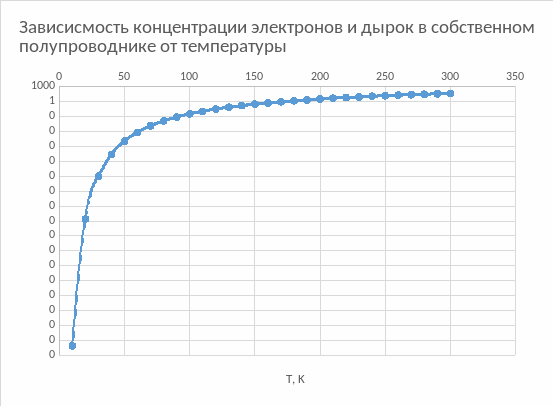
Задание 1. Найти положение уровня Ферми и температурную зависимость концентрации электронов и дырок в собственном полупроводнике при изменении температуры в интервале 0-300 K. Построить графики.

Положение уровня Ферми определяется по следующей формуле:

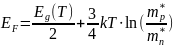
Ширина запрещённой зоны также зависит от температуры:

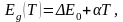
_{Поскольку нам неизвестен коэффициент зависимости ширины запрещённой зоны от температуры, мы не сможем определить значение 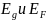при .}

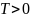_{Определим энергию Ферми для температуры T = 0:}

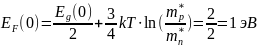
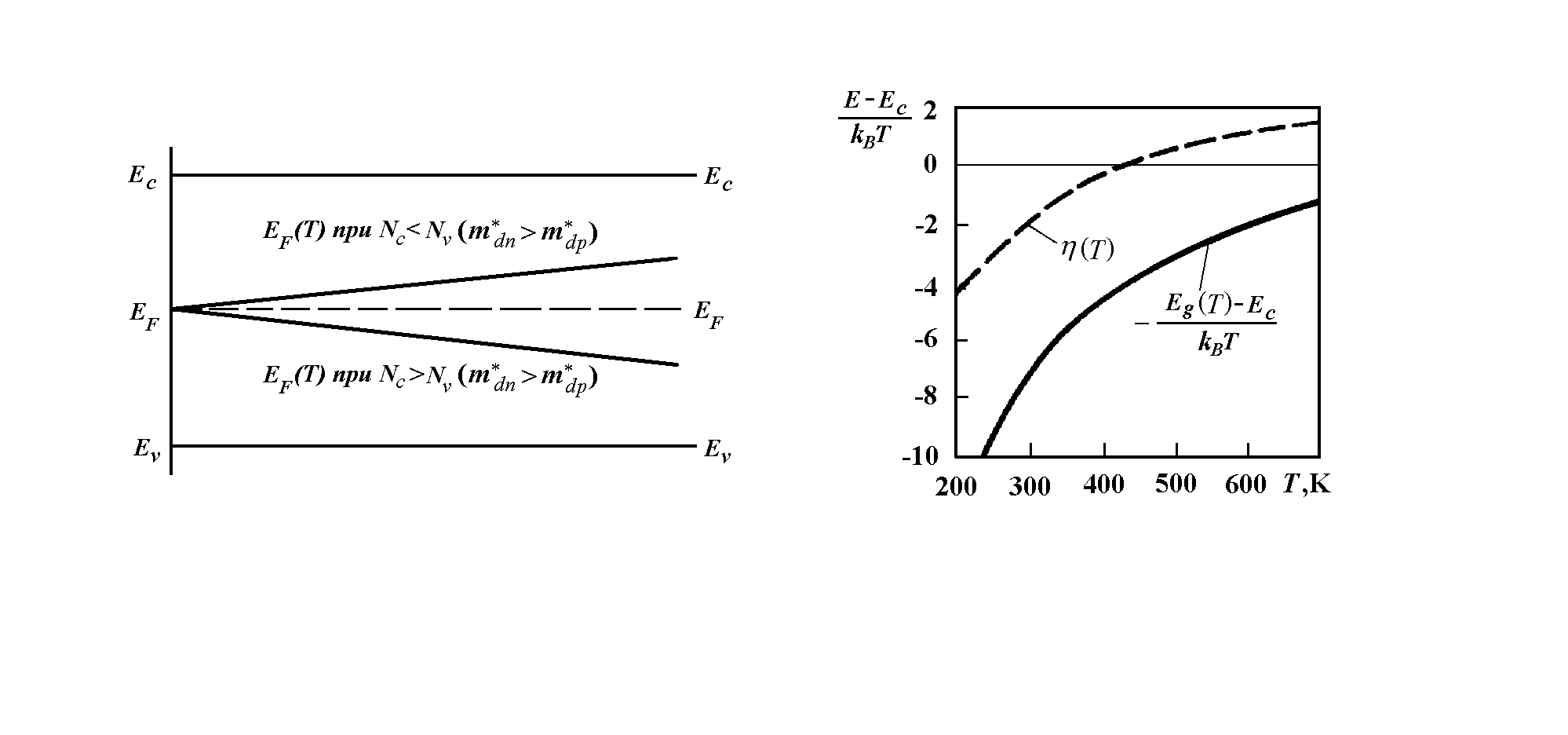
При Т = 0 уровень Ферми в собственном полупроводнике находится в середине запрещённой зоны, а с ростом температуры движется к той зоне, в которой эффективное число состояний, а значит, и эффективная масса для плотности состояний меньше.

Если не учитывать температурную зависимость ширины запрещённой зоны, то энергия Ферми для крайней температуры будет:

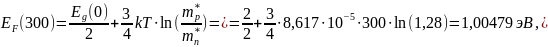
где 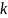= 8,617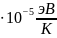 - постоянная Больцмана.

В собственном проводнике 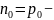концентрации электронов и дырок равны и не зависят от положения уровня Ферми.

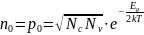
Определим эффективные плотности состояний в валентной зоне и зоне проводимости:

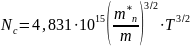
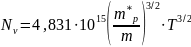
Тогда :

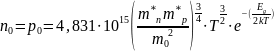
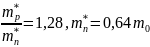- из исходных данных, тогда

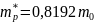
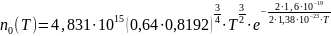
T, K	n(T)		T, K	n(T)		T, K	n(T)
0	-		110	0,011658969		220	7,044203778
10	7,42559E-50		120	0,032262965		230	9,540438843
20	2,50489E-24		130	0,077190378		240	12,63860364
30	1,0482E-15		140	0,164602956		250	16,41807513
40	2,4533E-11		150	0,31992824		260	20,95902692
50	1,11499E-08		160	0,576414786		270	26,34173266
60	6,97052E-07		170	0,975245553		280	32,64596275
70	1,39203E-05		180	1,565262266		290	39,95047181
80	0,000135574		190	2,402384116		300	48,33257147
90	0,000815403		200	3,548812379
100	0,003491675		210	5,0721065

Изменяя значения Т от 0 до 300К построим зависимость концентрации от температуры в осях

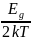
Задание 2. Рассчитать и построить зависимость концентрации электронов в том же интервале температур, если E_g(T) = E_g(0) - ξT, N_d = 5·10¹⁸ см^-3, N_c ≈ 2,5·10¹⁹ см^-3, N_v = 2,3N_c.

Если проводник остаётся собственным, то

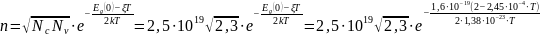
Изменяя значения Т от 0 до 300К построим зависимость концентрации от температуры в осях

T, K	n(T)		T, K	n(T)		T, K	n(T)
0	-		110	0,000415035		220	0,08069679
10	6,96057E-50		120	0,000998956		230	0,101477109
20	1,04505E-24		130	0,002100496		240	0,125195079
30	2,5781E-16		140	0,003971793		250	0,151882906
40	4,04932E-12		150	0,006898627		260	0,181541127
50	1,33362E-09		160	0,011183217		270	0,214142527
60	6,36011E-08		170	0,017127266		280	0,249636105
70	1,00541E-06		180	0,02501729		290	0,287950914
80	7,97086E-06		190	0,035113265		300	0,328999664
90	3,98889E-05		200	0,047640802
100	0,000144654		210	0,062786622

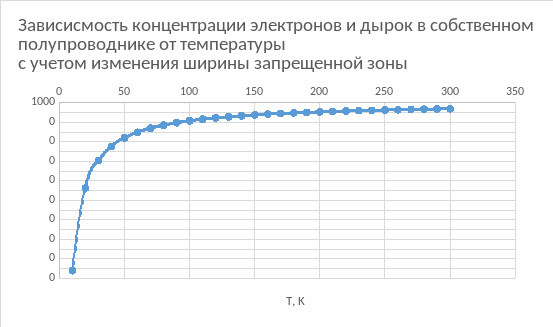
Поскольку в этом задании нам известен температурный коэффициент, построим зависимость изменения уровня Ферми от температуры:

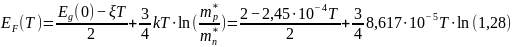
T, K	Eф, эВ		T, K	Eф, эВ		T, K	Eф, эВ
0	1		110	0,986540954		220	0,973065954
10	0,998790954		120	0,985315954		230	0,971840954
20	0,997565954		130	0,984090954		240	0,970615954
30	0,996340954		140	0,982865954		250	0,969390954
40	0,995115954		150	0,981640954		260	0,968165954
50	0,993890954		160	0,980415954		270	0,966940954
60	0,992665954		170	0,979190954		280	0,965715954
70	0,991440954		180	0,977965954		290	0,964490954
80	0,990215954		190	0,976740954		300	0,963265954
90	0,988990954		200	0,975515954
100	0,987765954		210	0,974290954

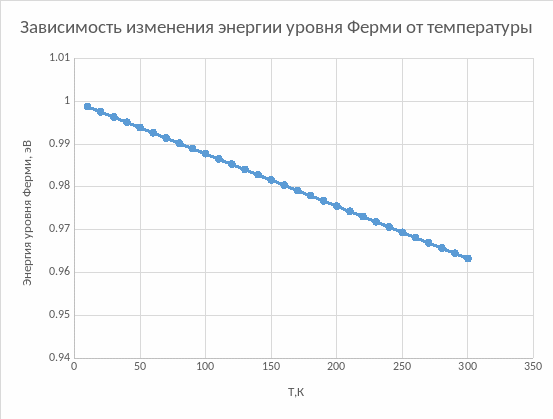
Если в проводник ввести донорную примесь, то для электронов донора, чтобы оказаться в зоне проводимости, достаточно получить дополнительную энергию, примерно равную энергии ионизации E_d « Eg. Поэтому концентрацию носителей заряда в донорном полупроводнике при невысокой температуре определяют электроны донора:

T, K	n(T)		T, K	n(T)		T, K	n(T)
0	-		110	0,38966142		220	0,660031414
10	1,03073E-05		120	0,425435385		230	0,675329605
20	0,003394631		130	0,458259168		240	0,689664237
30	0,023442775		140	0,488402228		250	0,703120677
40	0,061605178		150	0,516125418		260	0,715774929
50	0,109997328		160	0,54167109		270	0,727694801
60	0,161892009		170	0,565259387		280	0,738940925
70	0,213360229		180	0,587087734		290	0,749567635
80	0,262439687		190	0,607331912		300	0,759623734
90	0,308293388		200	0,62614784
100	0,350680785		210	0,643673593

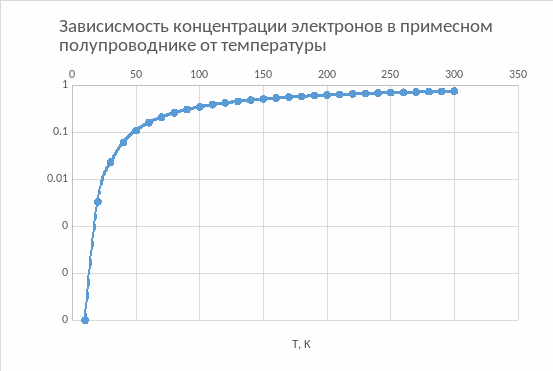
Вывод: В ходе данной работы был определён уровень Ферми при T=0, также построен график изменения концентрации электронов и дырок с изменением температуры в заданном интервале, как в собственном так и примесном проводнике. Концентрация электронов и дырок в собственном полупроводнике оказывается независимой от положения уровня Ферми и растёт с температурой по экспоненциальному закону.

При увеличении температуры полная концентрация электронов в примесном полупроводнике будет определяться суммой собственных и примесных носителей. В связи с тем, что уровень донора имеет энергию ионизации много меньше, чем ширина запрещённой зоны, при увеличении температуры первыми ионизуются доноры, а затем усиливаются переходы собственных электронов из валентной зоны в зону проводимости.