ИРС_3
.docxМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение
высшего образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Инженерная школа новых производственных технологий
Обеспечивающее подразделение: Отделение материаловедения
Направление подготовки: 12.03.02 Оптотехника
ООП: Оптико-электронные приборы и системы
ИНДИВИДУАЛЬНАЯ РАБОТА СТУДЕНТА №3
дисциплина "Физические основы источников излучения"
Вариант 4
Выполнил:
студент группы _________________
Проверил:
доктор ф-м.н., профессор ОМ ИШНПТ _________________ В.Ф. Штанько
Томск - 2023
Вариант 4 - N+3
Задание 1. Определить смещенные термы для двухэлектронных атомов (ионов) при одновременном возбуждении двух электронов для главных квантовых чисел от n до n + 2.
Порядковый номер N в периодической системе равен 7. Т.к он ионизован трижды, то сумма электронов равна 4.
Заполнение
электронных состояний происходит в
следующем порядке, в соответствии с
правилом Клечковского: 1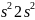
Составим
таблицу для двух электронов в p-состоянии.
Пусть 1й электрон не изменяет своего
состояния и
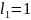
L
|
0 |
1 |
2 |
0 |
|
P |
|
1 |
S |
P |
D |
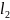
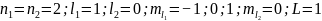
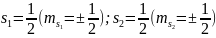
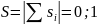
При
S=0:
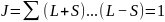
Мультиплетность: 2S+1=1
При
S=1:
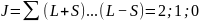
Мультиплетность: 2S+1=3
Термы данного состояния: 1P1; 3P0; 3P1; 3P2
|
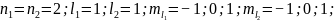
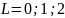
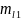
1 |
0 |
-1 |
1 |
(2) |
1 |
0 |
0 |
1* |
(0) |
-1 |
-1 |
0* |
-1* |
(-2) |
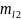
, то в данном случае
выбор результирующих состояний, которые
не противоречили бы принципу Паули,
можно сделать следующим образом. Заполним
таблицу, в которой приводим все возможные
значения ml1
и ml2
и соответствующие им значения mL
= ml1
+ ml2.
Так как с точки зрения квантовой механики
состояния, получающиеся в результате
перестановки электронов, неразличимы,
то все те значения mL,
которые получаются в результате
перестановки, из таблицы следует
исключить.
Если значение mL = 0 получается один раз в результате того, что ml1 = 1, ml2 = - 1, а второй раз в результате того, что ml1 = -1, ml2 = 1, то одно из значений mL = 0 надо отбросить. Из оставшихся значений mL выбираем совокупности значений, начинающихся от некоторого + mL мах и кончающихся - mL мах. Каждая совокупность значений соответствует значению L = mL мах. По принципу Паули все найденные таким способом L отвечают возможным состояниям атома, если при этом ms1 ms2 . Если ms1 = ms2 , то следует сохранить лишь те значения mL , которым соответствуют ml1 ml2 .
Одинаковые значения mL , выделенные (*), соответствуют состояниям, отличающимся друг от друга лишь перестановкой электронов. Такие состояния неотличимы друг от друга. Поэтому значения mL , выделенные (*), следует отбросить. Оставшиеся значения mL образуют две совокупности: mL = 2, 1, 0, -1, -2; mL = 0. Этим совокупностям значений mL соответствуют значения квантового числа полного орбитального момента L = 2 и L = 0. Эти состояния возможны, если ms1 ms2 , а, следовательно, указанные значения L возможны при S = 0, т.е. для системы синглетных термов.
При ms1 = ms2 мы должны отбросить в таблице те значения mL , которые соответствуют одинаковым значениям ml1 и ml2 (эти значения взяты в таблице в скобки). Тогда остается одна совокупность значений mL: mL = 1, 0, -1, которой соответствует L = 1. Так как при ms1 = ms2 квантовое число S = 1, то имеем триплетное состояние.
Таким
образом, при
,
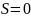L=0,2, мультиплетность
2S+1=1,
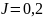
Получим 2 состояния атома 1S0 и 1D2
При
,
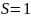L=1, мультиплетность
2S+1=3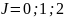
Получим 3 состояния атома 3Р2, 3Р1, 3Р0
Т.к.
достигнут предел по l
= n
- 1, то
повысим
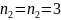и запишем термы при
:
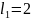L
|
0 |
1 |
2 |
3 |
4 |
0 |
|
|
D |
|
|
1 |
|
P |
D |
F |
|
2 |
S |
P |
D |
F |
G |
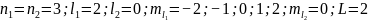
При
S=0:
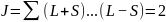
Мультиплетность: 2S+1=1
При
S=1:
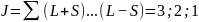
Мультиплетность: 2S+1=3
Термы данного состояния: 1D2; 3D1; 3D2; 3D3
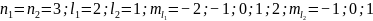
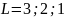
При S=0:
Мультиплетность: 2S+1=1
При
S=1:
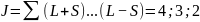3;2;1 2;1;0
Мультиплетность: 2S+1=3
Термы данного состояния: 1P1; 1D2; 1F3; 3P012; 3D123; 3F234
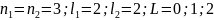
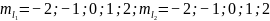
Т.к.
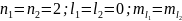, необходимо
сделать отбор в соответствии с принципом
Паули:
|
2 |
1 |
0 |
-1 |
-2 |
2 |
(4) |
3 |
2 |
1 |
0 |
1 |
3* |
(2) |
1 |
0 |
-1 |
0 |
2* |
1* |
(0) |
-1 |
-2 |
-1 |
1* |
0* |
-1* |
(-2) |
-3 |
-2 |
0* |
-1* |
-2* |
-3* |
(-4) |
*
- для неразличимых значений
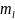
( ) - для одинаковых значений
Из таблицы видно, что при ms1 ms2 надо использовать следующие совокупности значений mL :
mL = 4, 3, 2, 1, 0, - 1, -2, -3, -4;
mL = 2, 1, 0, -1, -2;
mL = 0.
Данным совокупностям отвечают значения L = 4, 2, 0, т.е. синглетные термы 1G4, 1D2, 1S0. При ms1 = ms2 надо отбросить значения mL поставленные в скобки, поскольку они соответствуют состояниям с ml1 = ml2, что находится в противоречии с принципом Паули. Тогда остаются совокупности: mL = 3, 2, 1, 0, -1, -2, -3; mL = 1, 0, -1, которым отвечают значения L = 3,1 и, следовательно, триплетные термы 3F234 и 3Р012.
Т.к.
достигнут предел по l
= n
- 1, то
повысим
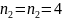и запишем термы при
:
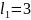L
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
|
|
|
F |
|
|
|
1 |
|
|
D |
F |
G |
|
|
2 |
|
P |
D |
F |
G |
H |
|
3 |
S |
P |
D |
F |
G |
H |
I |
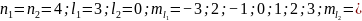0
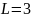
В
данном случае, электроны имеют различные
орбитальные числа, соответственно,
возможно
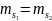
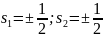
При
S=0:
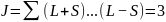
Мультиплетность: 2S+1=1
При
S=1:
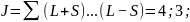2
Мультиплетность: 2S+1=3
Термы данного состояния: 1F3; 3F2; 3F3; 3F4
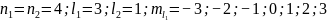
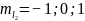
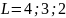
В данном случае, электроны имеют различные орбитальные числа, соответственно, возможно
При S=0:
Мультиплетность: 2S+1=1
При
S=1:
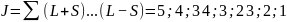
Мультиплетность: 2S+1=3
Термы данного состояния: 1D2; 1F3; 1G4; 3D123; 3F234; 3G345
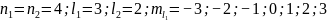
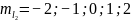
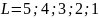
В данном случае, электроны имеют различные орбитальные числа, соответственно, возможно
При
S=0:
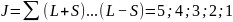
Мультиплетность: 2S+1=1
При
S=1:
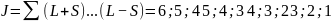
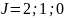
Мультиплетность: 2S+1=3
Термы данного состояния: 1P1; 1D2; 1F3; 1G4; 1H5; 3P012; 3D123 ; 3F234; 3G345; 3H456
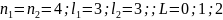
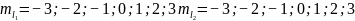
Т.к.
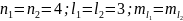, необходимо
сделать отбор в соответствии с принципом
Паули:
|
3 |
2 |
1 |
0 |
-1 |
-2 |
-3 |
3 |
(6) |
5 |
4 |
3 |
2 |
1 |
0 |
2 |
5* |
(4) |
3 |
2 |
1 |
0 |
-1 |
1 |
4* |
3* |
(2) |
1 |
0 |
-1 |
-2 |
0 |
3* |
2* |
1* |
(0) |
-1 |
-2 |
-3 |
-1 |
2* |
1* |
0* |
-1* |
(-2) |
-3 |
-4 |
-2 |
1* |
0* |
-1* |
-2* |
-3* |
(-4) |
-5 |
-3 |
0* |
-1* |
-2* |
-3* |
-4* |
-5* |
(-6) |
* - для неразличимых значений
( ) - для одинаковых значений
Из таблицы видно, что при ms1 ms2 надо использовать следующие совокупности значений mL :
mL = 6, 5, 4, 3, 2, 1, 0, - 1, -2, -3, -4,-5,-6
mL = 4, 3, 2, 1, 0, -1, -2, -3, -4
mL = 2, 1, 0, -1, -2
mL = 0
Данным совокупностям отвечают значения L = 6, 4, 2, 0, т.е. синглетные термы 1I6, 1G4, 1D2, 1S0. При ms1 = ms2 надо отбросить значения mL поставленные в скобки, поскольку они соответствуют состояниям с ml1 = ml2, что находится в противоречии с принципом Паули. Тогда остаются совокупности:
mL = 5, 4, 3, 2, 1, 0, - 1, -2, -3, -4,-5
mL = 3, 2, 1, 0, -1, -2, -3
mL = 1, 0, -1
которым отвечают значения L = 5, 3,1 и, следовательно, триплетные термы 3H543 , 3F432 и 3Р210.
Общая
таблица термов (из ИРС 2 и ИРС 3)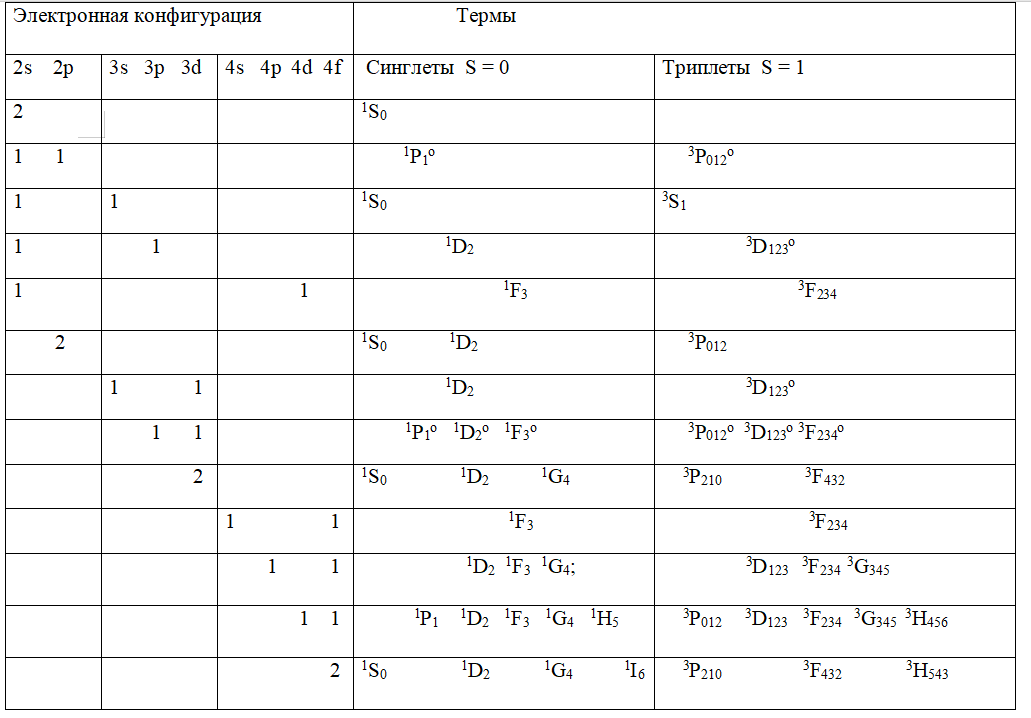
Список литературы:
Штанько В.Ф. Введение в атомную и молекулярную спектроскопию. - Томск: Изд-во Томского Политехнического университета, 2008.-164 с. - ISBN 5-98298-357-8.