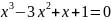Санкт-Петербургский политехнический университет Петра Великого

Институт машиностроения, материалов и транспорта

Высшая школа машиностроения

ОТЧЕТ

по лабораторной работе №5

Дисциплина: Цифровая культура

Тема: Решение уравнений и систем линейных уравнений в табличном процессоре Microsoft Excel

(Вариант 1)

Студент группы 3331505/10001 Гричачина А.А.

Преподаватель Ситкин Д.С.

Санкт-Петербург

2022 г.

Цель работы

Приобретение умений решения уравнения и систем линейных алгебраических уравнений средствами программы Excel.

Задание

1. Р 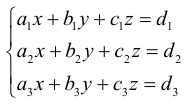ешить систему уравнений:

для значений коэффициентов, представленных в таблице 1.

Таблица 1 – Коэффициенты уравнений

Вариант	a1	a2	a3	b1	b2	b3	c1	c2	c3	d1	d2	d3
1	1,1	5,0	2,2	2,0	-4,5	1,3	-1,0	1,8	-3,3	2,0	0	-5,1

2. Решить уравнение с относительной погрешностью 0,001 в соответствии с вариантом задания таблицы 2.

Таблица 2 – Вариант уравнения

Вариант	Уравнение
1

Рабочий лист Excel с решениями СЛАУ способом Крамера и матричным методом

На листе Excel сформированы таблицы с исходными данными, по ним построены четыре таблицы, необходимые для реализации метода Крамера, с использованием ссылок на исходные значения.

В ячейках F7, F11, F15 и F19, введены соответственно формулы: =МОПРЕД(B6:D8); =МОПРЕД(B10:D12); =МОПРЕД(B14:D16) и =МОПРЕД(B18:D20), посчитавшие значения определителей. Для вычисления значения х, у, z в ячейку I11 введена формула, соответствующая методу Крамера: =ЕСЛИ($F$7<>0;F11/$F$7;решение не может быть найдено); и скопирована в I15, I19. Оформление решения представлено на рисунке 1.

Д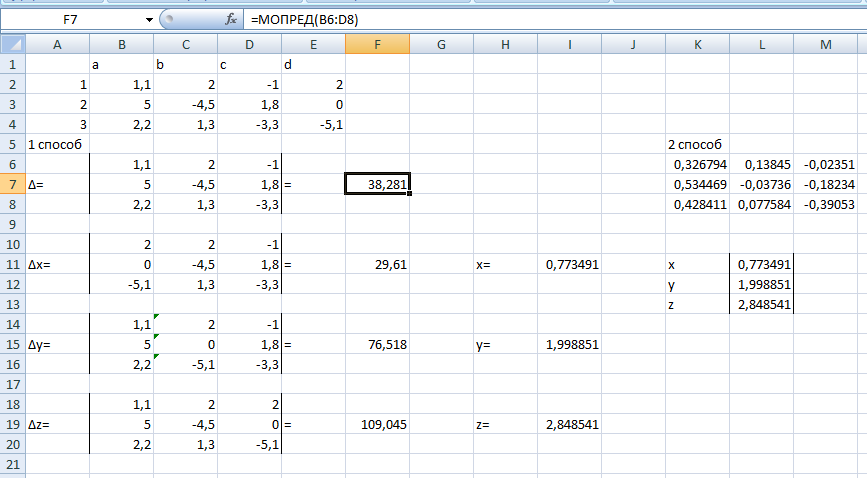

Рисунок 1– Решение системы двумя способами

ля матричного способа в выделенный диапазон K6:M8 была написана формула =МОБР(B2:D4) и введена с помощью одновременного нажатия клавиш SHIFT+CTRL+ENTER. Затем в диапазон L11:L13 была написана формула =МУМНОЖ(K6:M8;E2:E4), ввод закончен тем же сочетанием. Оформление решений представлено на рисунке 1.

Рабочие листы Excel с детализацией решения уравнения

С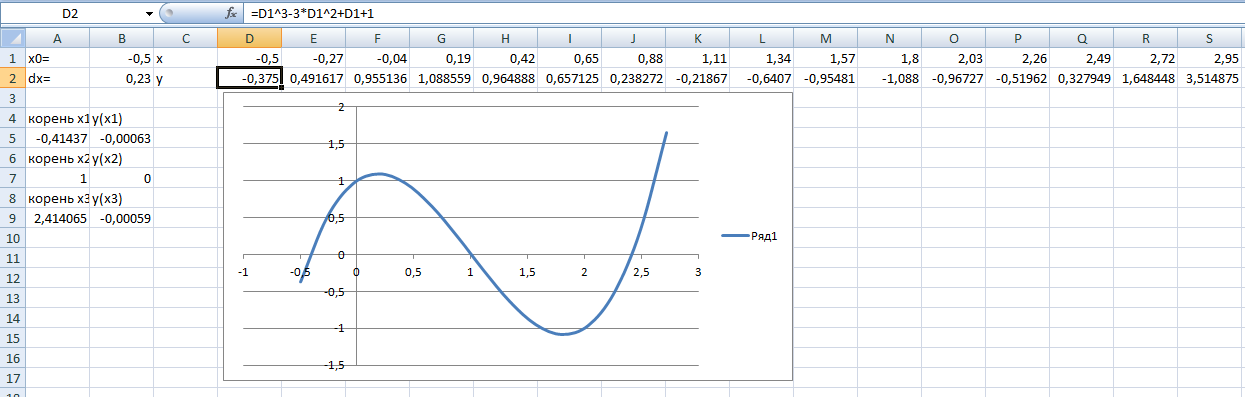

Рисунок 2 ­– Определение числа корней и их примерного значения

начала были введены исходные формулы, по ним рассчитаны значения x и y растянутой формулой =D1+$B$2 в диапазоне F1:S1 и формулой =D1^3-3*D1^2+D1+1 в диапазоне D2:S2 соответственно(рисунок 2). По построенному графику и изменению исходных данных, получен график, на котором видно 3 корня (рисунок 2).

Д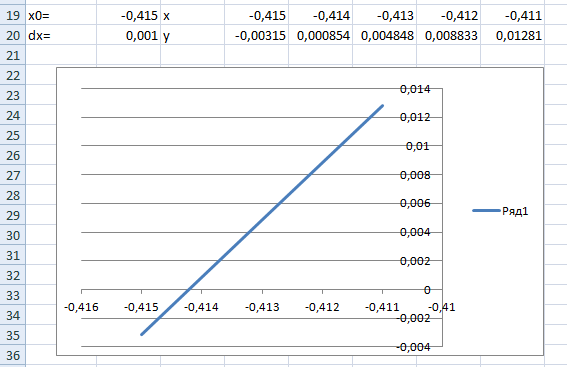 ля всех найденных корней построен укрупненный график (рисунок 3-5). Рисунок 3 – Графическое определение значения корня 1

Р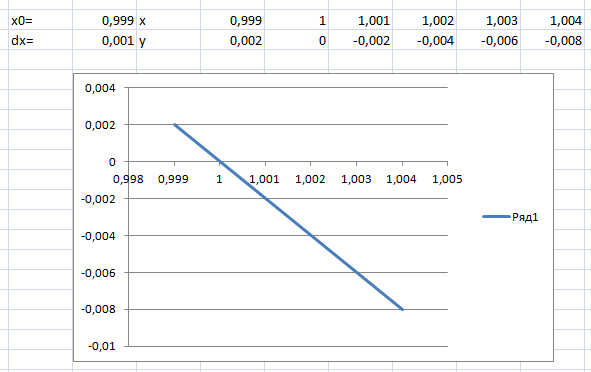 исунок 4 – Графическое определение значения корня 2

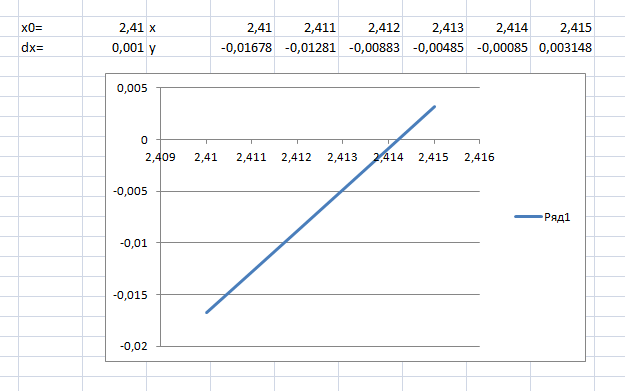Рисунок 5 – Графическое определение значения корня 3

П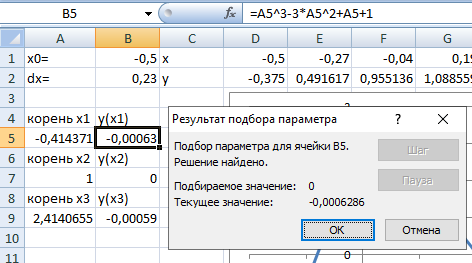 риближенное значение корня было занесено с рисунка 3 в ячейку А5, а в ячейку В5 записана формулу, по которой вычислено значение у(х), т.е.: =A5^3-3*A5^2+A5+1, аналогично для корней 2 и 3 в ячейки A7, A9 внесены значения корней, а в B7,B9 скопирована формула. Далее итерационным (повторяющимся) способом Подбор параметра был осуществлён поиск корней с заданной точностью. Результат подбора корней представлен на рисунке 6.

Рисунок 6 – Полученные значения корней с использованием подбора параметра

Выводы по работе

С помощью формулы в Excel =МОПРЕД можно считать определитель матрицы, = МОБР – находить обратную матрицу, =МУМНОЖ – перемножать матрицы. Данные формулы можно применять для решения СЛАУ методом Крамера и обратной матрицы. С помощью инструмента Подбор параметра можно найти значения, которые нужно ввести в одиночную формулу, чтобы получить желаемый (известный) результат. Данный инструмент можно применять для решения уравнений.