
Rabota_2_Algoritmy
.pdfЛабораторная работа №2
АЛГОРИТМЫ И ОСНОВЫ АЛГОРИТМИЗАЦИИ
Цель работы – приобретение умений проектирования, представления в виде блок-схемы и чтения вычислительных алгоритмов решения задач.
Понятие алгоритма и предъявляемые к нему требования
Алгоритм – описание способа решения поставленной задачи путём разбиения её на конечную последовательность элементарных действий. Под элементарным действием понимают такое действие, которое не требует дополнительных пояснений. При этом алгоритм должен быть:
–полным – учитывать все возможные ситуации, которые могут встретиться по ходу решения задачи;
–однозначным – не допускать действия, имеющие неопределённое толкование;
–определённым – повторять результаты при повторе исходных данных;
–корректным – давать правильные результаты при различных исходных данных;
–конечным – давать результат за конечное число шагов;
–массовым – пригодным для использования для решения сходных задач;
–эффективным и оптимальным – давать результат за минимальное число шагов с использованием минимальных ресурсов.
Способы представления алгоритма
Существует несколько способов представления алгоритмов: словесный, формульно-словесный, табличный, операторный, графический. Наиболее распространенный графический, т.е. в виде блок-схемы.
Блок-схема алгоритма графическое изображение алгоритма в виде геометрических фигур (блоков), соединённых линиями. Внутри блока записывают действие, которое необходимо выполнить, или условие, которое нужно проверить. В таблице 1 представлены элементы блок-схем.
1
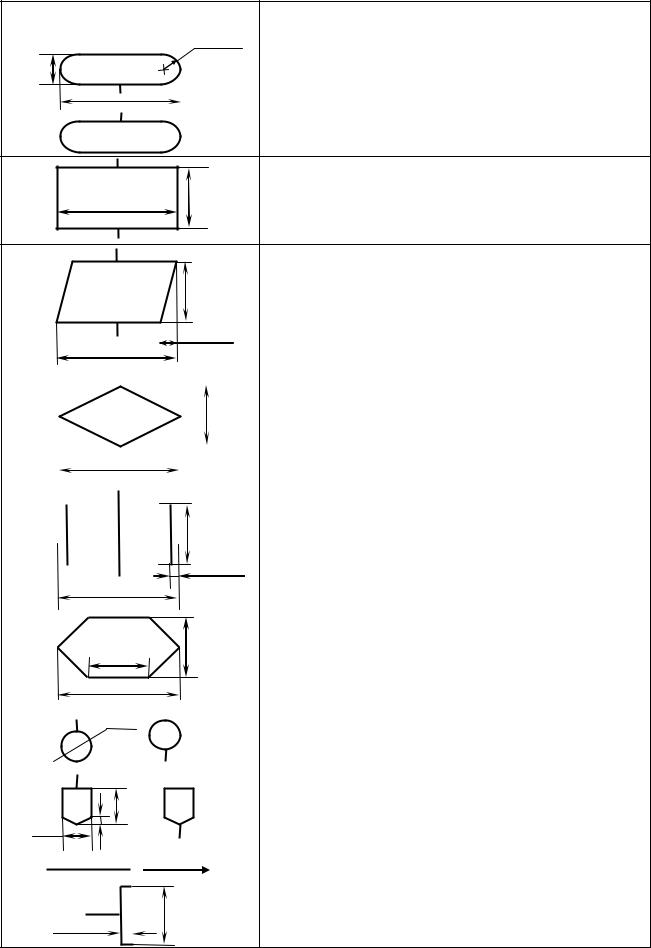
Таблица 1 - Элементы блок-схем алгоритмов
|
Элемент блок-схемы |
Описание |
||
|
|
|
R 0,25a |
|
0,5a |
начало |
|
|
Начало и конец схемы |
|
||||
|
2a |
|
|
|
|
|
|
|
|
конец |
|
|
2a |
a |
Действие (процесс) или группа действий |
|
|
|
|
|
|
|
a |
Ввод или вывод данных |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,25a |
|
||
|
|
|
|
|
|
|
|
|||
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет a |
Условие. Определение направления движения |
||
|
|
|
|
|
|
|
||||
|
|
да |
|
|
|
|
|
|
|
потока в зависимости от условия |
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
Предварительно описанный процесс. Ссылка |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0,15a |
на действия, описанные в другом алгоритме |
||
|
|
|
|
|
|
|
(подпрограмму). |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
Подготовка. Границы изменения счётчика в |
|||
|
|
|
|
|
|
|
|
счётном операторе цикла |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5a |
|
|
|
|
|
Соединитель. Связывает разделённые части |
||
|
|
|
|
|
|
|
|
|
|
схемы, находящиеся на одной странице. Внут- |
|
|
|
|
|
|
|
|
|
|
ри указывают номер соединения |
|
|
|
|
|
|
|
|
|
|
Межстраничный соединитель. Связывает раз- |
|
|
|
0,6a |
|
|
|
|
|
делённые части схемы, находящиеся на раз- |
|
0,5a |
|
|
|
|
|
|
|
|
ных страницах. Внутри указывают номер со- |
|
|
|
0,2a |
|
|
|
|
|
|
единения и страницу продолжения схемы |
|
|
|
|
|
|
|
|
|
|
|
Линии потока |
|
|
|
|
|
a |
Комментарий. Пояснение к блоку или запись |
||||
|
5 мм |
|
|
|
действий, не поместившихся внутри блока |
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2
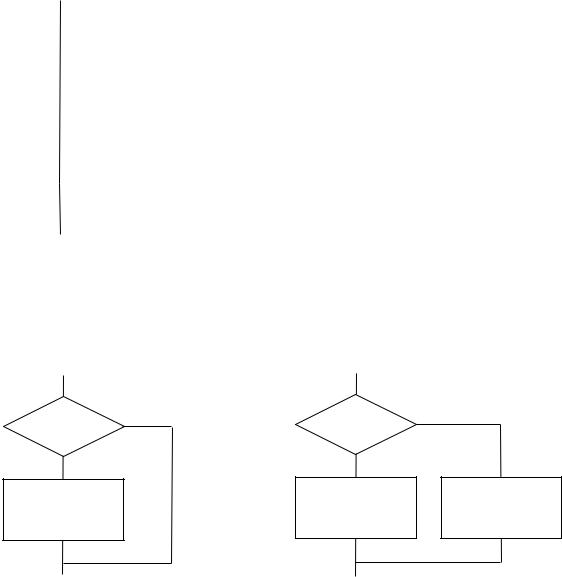
Значение а выбирают из ряда 10, 15, 20 мм или увеличивают на число кратное пяти. Расстояние между линиями потока должно быть не менее 3 мм,
между другими частями схемы – не менее 5 мм.
Виды алгоритмов
Существует три основных вида алгоритмов: линейный, разветвляющийся,
циклический (повторений). В программировании конструкции, которые реали-
зуют данные алгоритмы, называют основными управляющими конструкциями.
Их всего три: линейное следование; ветвление; цикл. С их помощью можно ре-
ализовать (описать) любой алгоритм.
|
|
|
Линейный алгоритм – алгоритм, в котором действия |
|
|
|
выполняются друг за другом в порядке записи. На рисун- |
Действие 1 |
|
ке 1 представлен в общем виде фрагмент блок-схемы ли- |
|
|
|
||
|
|
|
нейного алгоритма. Данный алгоритм является самым |
|
|
||
|
|
|
простым. |
Действие 2 |
|
||
|
Разветвляющийся алгоритм – алгоритм, в котором |
||
|
|
|
|
|
|
|
на определённом этапе выбор очередного выполняемого |
|
|
|
|
|
|
|
действия производится в результате анализа условия. Раз- |
|
|
|
|
Действие N |
|
личают неполную форму (фрагмент блок-схемы на рисун- |
|
|
|
|
ке 2 а) и полную форму (фрагмент блок-схемы на рисунке |
|
|
|
|
|
|
|
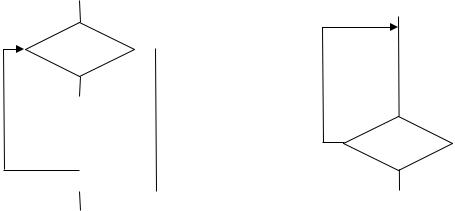
2 б) разветвляющегося алгоритма. |
Рисунок 1 |
|
||
|
|
||
условие |
нет |
условие |
нет |
|
|
||
да |
|
да |
|
Действие |
|
Действие 1 |
Действие 2 |
а |
Рисунок 2 |
б |
|
|
3
Вкачестве условия в общем случае выступает логическое высказывание,
априменительно к математике или программированию в качестве условия обычно используют логическую переменную или выражение. В любом случае логическое высказывание, логическая переменная или выражение являются та-
ковыми, если могут принимать только одно из двух значений «истина» или
«ложь». В первом варианте, если условие приняло значение «истина» (ветвь
«да»), выполняется действие, в противном случае, т.е. условие приняло значе-
ние «ложь» (ветвь «нет»), действие пропускается. Во втором варианте соответ-
ственно выполняется либо первое действие, либо второе.
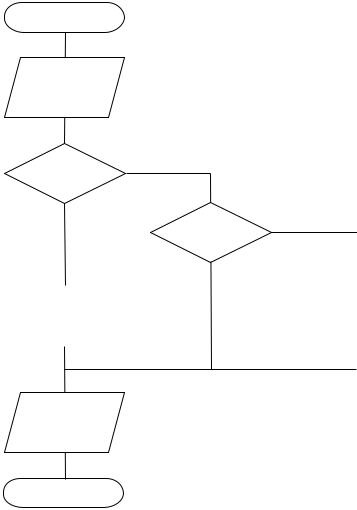
Повторяющийся (циклический) алгоритм алгоритм, в котором резуль-
тат достигается многократным выполнением одного и того же действия (дей-
ствий). Однократный проход такого действия (действий) называют итерацией,
а само повторяющиеся действие (действия), называют телом цикла. Различают циклические алгоритмы с предварительной проверкой условия (с предуслови-
ем) и последующей проверкой условия (с постусловием). В первом случае сна-
чала проверяется условие (вычисляется его значение), и, если оно приняло зна-
чение «истина», то выполняется тело цикла. Тело цикла выполняется всякий следующий раз, пока условие принимает значение «истина» (ветвь «да»). Соот-
ветствующий фрагмент блок-схемы представлен на рисунке 3 а. Если условие принимает значение «ложь» с самого начала, то тело цикла не выполнится ни разу (ветвь «нет»). Во втором случае сначала выполняется действие, а затем проверяется условие, и в зависимости от его значения происходит возврат к
|
|
|
|
|
|
|
|
началу |
тела цикла |
|
условие |
нет |
|
|
|
или выход из цикла |
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||
да |
|
|
|
|
|
Действие |
(рисунок 3 |
б). При |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
данной |
конструкции |
|
|
|
|
|
|
|
|
|
|||
Действие |
|
|
|
нет |
|
тело цикла |
выпол- |
|||
|
|
|
|
|
условие |
|||||
|
|
|
|
|
(да) |
|||||
|
|
|
|
|
да (нет) |
нится, |
по |
крайней |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мере, один раз. |
||
|
а |
|
|
Рисунок 3 |
|
|
б |
|||
|
|
|
|
|
|
|
|
|||
4
Общие принципы построения блок-схем алгоритмов
Любая блок-схема (если представляется не фрагмент схемы) начинается с элемента «Начало», который имеет только один выход и не имеет входов. Сле-
дующим элементом в большинстве схем является параллелограмм, обозначаю-
щий ввод данных из внешней среды, необходимых для реализации алгоритма.
Завершается любая блок-схема одним элементом «Конец», у которого есть только один вход и нет выходов. Предпоследний элемент схемы, как правило,
параллелограмм, обозначающий в данном случае уже вывод данных, т.е. ре-
зультаты работы алгоритма. Направление движения по схеме определяется ли-
ниями потока, которые могут быть либо вертикальными, либо горизонтальны-
ми. Допускается изгиб линии потока только под прямым углом. Схему реко-
мендуется строить так, чтобы движение по ней осуществлялось сверху вниз и слева направо, в контурах – по часовой стрелке, вход в элемент следует осу-
ществлять сверху или слева, выход – снизу или справа, в противном случае на линии потока нужно ставить стрелки для указания направления движения. Сле-
дует избегать пересечения соединительных линий (если это не предполагается алгоритмом), для этого их можно разрывать, используя соединители (см. таб-
лицу). Каждый элемент должен содержать пояснение, что необходимо сделать,
пустые элементы не допускаются. Все математические выражения, арифмети-
ческие и логические операции, условия, операции присвоения значения долж-
ны быть записаны в универсальном, понятном всем, виде, т.е. на математиче-
ском языке, а не в привязке к какому-либо языку программирования.
При построении алгоритмов решения сложных задач можно разбить их на подзадачи, для каждой из которых описывается свой алгоритм, а затем пред-
ставляется общая блок-схема с укрупнёнными этапами вычислений в виде предопределённых процессов (ссылок на ранее разработанные алгоритмы).
Пример 1
Разработаем алгоритм и представим его в виде блок-схемы для вычисле-
ния значения кусочной функции
5
x 1, |
x 2 |
|
|
2 x 1 . |
|
y 1, |
||
|
x 1 |
|
x, |
|
|
Функция задана на трёх интервалах разными зависимостями. Однако по-
скольку область определения функции не имеет разрывов, то достаточно про-
верить принадлежность введённого из внешней среды аргумента x только двум интервалам и, если он не принадлежит ни первому, ни второму, то остаётся только третий. Кроме того, если введённый аргумент не принадлежит первому интервалу, т.е. не выполняется условие x 2, это уже означает, что x 2 и
при проверке принадлежности аргумента x второму интервалу достаточно про-
верить только условие x < 1 (а не проверять условие 2 < x < 1). Таким обра-
зом алгоритм будет избавлен от избыточных проверок. После вычисления зна-
чения функции его необходимо вывести. Блок-схема алгоритма представлена на рисунке 4.
Начало
Ввод x
x 2 |
нет |
|
|
|
|
|
|
|
|
|
|
да |
|
|
нет |
||
|
|
x < 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
y = x 1 |
|
y = 1 |
|
y = x |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод у
Конец |
Рисунок 4 |
6
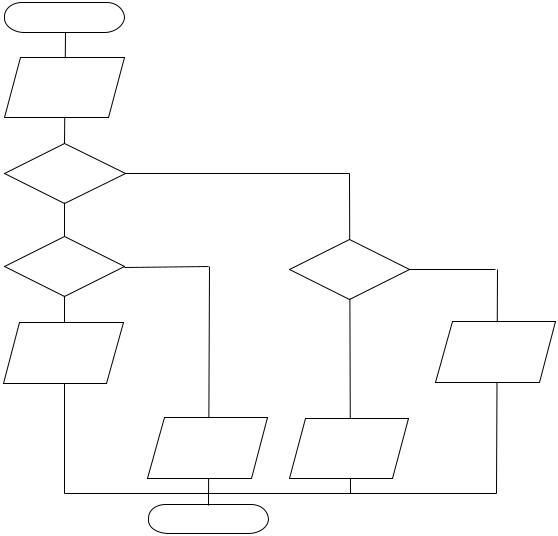
Представленная на рисунке 4 блок-схема представляет собой конструк-
цию вложенного ветвления (поливариантное ветвление).
Пример 2
Разработаем алгоритм вычисления другой кусочной функции
|
1 |
, х 1 |
|
|
|
|
||
y |
х |
|
х, х 2.
В данном случае функция задана на двух интервалах. Но в области опре-
деления есть разрывы: в точке х=0 функция не существует, а на интервале (1, 2)
функция не задана по условию. Все эти обстоятельства обязательно должны быть отражены в алгоритме, блок-схема которого представлена на рисунке 5.
Начало
Ввод x
нет
x1
да |
|
|
|
|
|
|
|
|
нет |
|
|
|
|
нет |
|
x = 0 |
|
|
|
|
|
x ≥ 2 |
|
|
|
|
|
|
|
||
да |
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
функция не |
|
у |
1 |
|
|
y = x |
функция не |
|
|
|
|
||||
существует |
|
х |
|
определена |
|||
|
|
|
|
||||
|
|
|
|
|
|
|
|
Вывод у |
Вывод у |
Конец
Рисунок 5
7
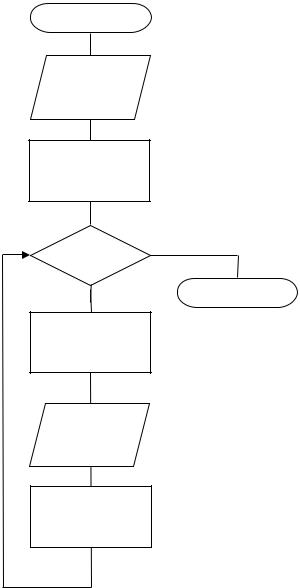
Отметим также, что если введённое значение аргумента х попало в разрыв об- |
||||||
ласти определения, то значение функции у не посчитано, а значит в ходе дви- |
||||||
жения по схеме необходимо обойти элемент «Вывод у». |
|
|||||
Пример 3 |
|
|
|
|
|
|
Разработаем алгоритм вычисления значений функции у=х2 для аргумента |
||||||
x на промежутке от a до b с шагом h и представим его в виде блок-схемы. Счи- |
||||||
таем, что границы диапазона a, b и шаг h задаются при вводе данных. |
||||||
|
|
|
|
Процесс последовательного вы- |
||
Начало |
|
|
числения значений функции у будет |
|||
|
|
|
|
иметь циклический характер. После |
||
Ввод |
|
|
ввода левой и правой границ диапазона |
|||
a, b, h |
|
|
a и b и шага приращения h, аргумент x |
|||
|
|
|
|
|||
|
|
|
|
должен |
последовательно |
принимать |
x = a |
|
|
значения: a, a+h, a+2h, …, b. Для каж- |
|||
|
|
|
|
|||
|
|
|
|
дого из этих значений вычисляется |
||
x b |
нет |
|
значение функции y и, вместе с соот- |
|||
|
|
ветствующим ему значением аргумента |
||||
|
|
|
|
|||
да |
|
|
Конец |
x, выводится на каждой итерации. По- |
||
|
|
|
|
|||
y = x |
2 |
|
|
сле этого значение аргумента x увели- |
||
|
|
|
|
|
|
|
|
|
|
|
чивается на шаг h и происходит воз- |
||
|
|
|
|
вращение к началу цикла. Если значе- |
||
Вывод |
|
|
ние x не превысило b, то осуществляет- |
|||
x и у |
|
|
||||
|
|
|
|
|
||
|
|
|
|
ся следующая итерация, и всё повторя- |
||
|
|
|
|
ется, пока x не превысит b. До входа в |
||
x = x + h |
|
|
цикл следует задать начальное значе- |
|||
|
|
|
|
|||
|
|
|
|
ние аргумента x=a, от которого в цикле |
||
|
|
|
|
начнёт увеличиваться значение x. Блок- |
||
Рисунок 6 |
|
|
схема алгоритма реализации постав- |
|||
|
|
|
|
|||
ленной задачи представлена на рисунке 6. |
|
|
||||
8
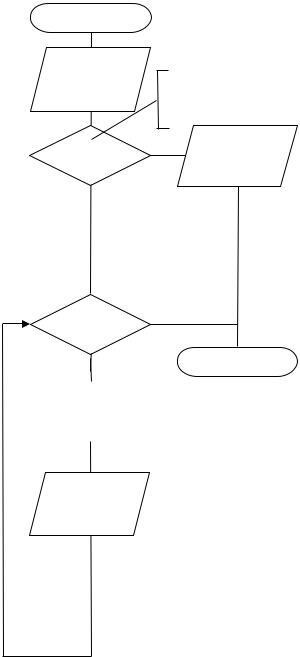
Однако представленный алгоритм не удовлетворяет одному из требова-
ний, предъявляемых к алгоритмам, – не учитывает все возможные ситуации,
которые могут встретиться. Так, если будет введён шаг h 0, цикл не сможет за-
вершиться. После получения аргументом начального значения x=a, он не будет в теле цикла (в ходе выполнения итераций) приближаться к правой границе диапазона (при a<b), условие завершения цикла х<b никогда не выполнится,
тем самым произойдёт зацикливание, чего допускать нельзя. Кроме этого в случае ввода значений границ диапазона таких, что a b условие входа в цикл примет значение «ложь» с самого нача-
|
Начало |
|
|
|
ла, тело цикла не выполнится ни разу, и |
|||
|
|
|
|
|
||||
|
Ввод |
|
|
|
по разработанному алгоритму никакого |
|||
|
|
|
|
|
|
|
|
|
|
a, b, h |
|
|
(h 0) или (a b) |
ответа не будет. Это не так критично, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
как зацикливание, но следовало бы вы- |
|||
|
|
да |
некоррект. |
вести соответствующее сообщение. Та- |
||||
|
|
|
|
исх данные |
||||
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
ким образом алгоритм, блок-схема ко- |
|||
|
|
|
|
|
торого |
представлена |
на |
рисунке 6, |
|
|
|
|
|
||||
|
x = a |
|
|
|
нужно дополнить: после ввода a, b и h |
|||
|
|
|
|
|
||||
|
|
|
|
|
необходимо добавить условие (элемент |
|||
|
|
|
|
|
||||
|
x b |
|
нет |
ромб) проверки значения шага и срав- |
||||
|
|
|
|
|||||
|
да |
|
|
Конец |
нения значений границ диапазона. |
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
Например можно записать логическое |
|||
|
y = x2 |
|
|
|
||||
|
|
|
|
выражение «(h 0) или (a b)», ветвь |
||||
|
|
|
|
|
«да» направить к элементу вывода дан- |
|||
|
|
|
|
|
||||
|
Вывод |
|
|
|
ных – |
параллелограмму, |
в котором |
|
|
|
|
|
|
|
|
|
|
|
x и у |
|
|
|
предусмотреть вывод |
«Некорректные |
||
|
|
|
|
|
исходные данные» и далее в элемент |
|||
|
x = x + h |
|
|
|
«Конец», а ветвь «нет» пустить далее |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по разработанному алгоритму (рисунок |
|||
|
|
|
|
|
7). Отметим, что в логическом выраже- |
|||
|
Рисунок 7 |
|
|
|
|
|
|
|
9
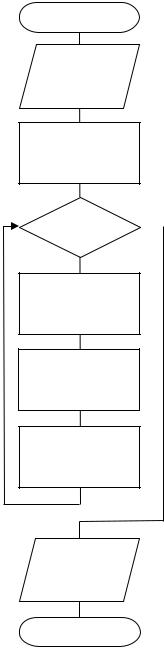
нии используется связка «или», т.к. если хотя бы одно условие выполнится, это приведёт к некорректной ситуации.
Пример 4
Разработаем алгоритм вычисления значения суммы
10
S sin(kx) .
k 1
Данное выражение представляет собой компактную форму записи сум-
мирования десяти слагаемых, т.е.
|
10 |
Начало |
sin(kx) sin x sin(2x) sin(3x) ... sin(10x). |
|
k 1 |
Ввод x
S0 = 0; k = 1
k 10 |
нет |
|
|
да |
|
ak = sin(kx)
Sk = Sk-1 + ak
k = k + 1
Вывод S10
Конец
Рисунок 8
Предлагается следующий алгоритм после-
довательного суммирования. Сначала вводится значение x, затем устанавливаются начальные зна-
чения суммы S=0 и номера слагаемого k=1. Далее организуется циклический процесс, в котором вы-
числяется текущее значение слагаемого ak, следую-
щим шагом оно добавляется к уже частично накоп-
ленной на предыдущей итерации сумме Sk-1 и запи-
сывается как Sk. После этого осуществляется пере-
ход к следующему номеру слагаемого, и всё повто-
ряется, пока не будут перебраны все десять слагае-
мых. В конечном итоге выводится накопленная за десять итераций сумма десяти слагаемых.
Следует отметить, что если реализация алго-
ритма будет осуществляться средствами вычисли-
тельно техники, то запоминать (хранить) промежу-
точные значения слагаемых и частичных сумм нет необходимости, т.к. важно только итоговое значе-
ние суммы, оно и выводится как результат.
10
