3.3 Определение инерциальных характеристик механизма

Инерциальными характеристиками являются: а) массы звеньев, б) осевые моменты инерции вращающихся звеньев; в) силы тяжести звеньев; г) проекции сил инерции и моменты сил инерции.

1. Массы звеньев

Масса звена находится как произведение погонной массы (μ=50 кг/м) на длину звена. Массу ползуна принимаем равной 10 кг. Рисунок 3.10

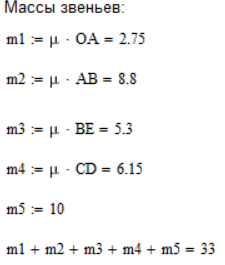
Рисунок 3. 10

2. Осевые моменты инерции вращающихся звеньев

Осевой момент инерции вычисляется по формуле:

Вычислим наши коэффициенты (Рис. 3. 11):

Рисунок 3. 11

3. Силы тяжести звеньев

Силы тяжести звеньев вычисляются по формуле:

,

где коэффициент свободного падения g=10 кг/с².

Вычислим наши переменные (Рис.3. 12):

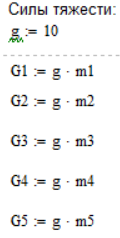
Рисунок 3. 12

4. Проекции сил инерции и моменты сил инерции

Для начала запишем закон движения центров масс, это нам понадобится далее. Рис. 3. 13

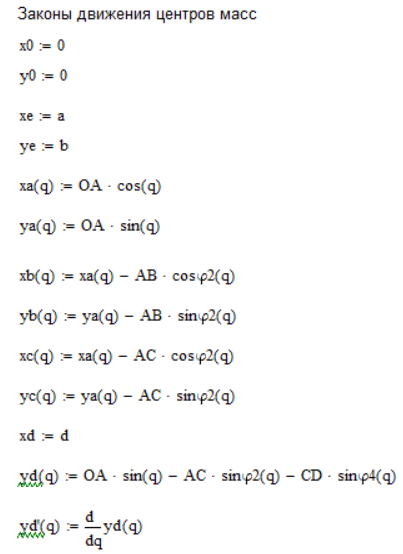
Рисунок 3. 13

Распишем центр масс звеньев в формульном виде (Рис. 3. 14):

Рисунок 3. 14

Распишем силы инерции (Рис. 3. 15):

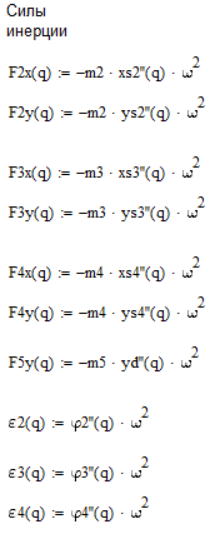
Рисунок 3. 15

Распишем моменты сил инерций (Рис. 3. 16):

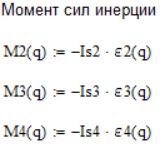
Рисунок 3. 16

3.4 Составление и решение уравнений кинетостатики

Для структурных групп механизма в направлении, обратном его образованию, составим уравнения кинетостатики и решим их.

Начнём с третьей структурной группы:

Расставим все силы, которые будут действовать на звенья 5 и 4. Рисунок 3.17

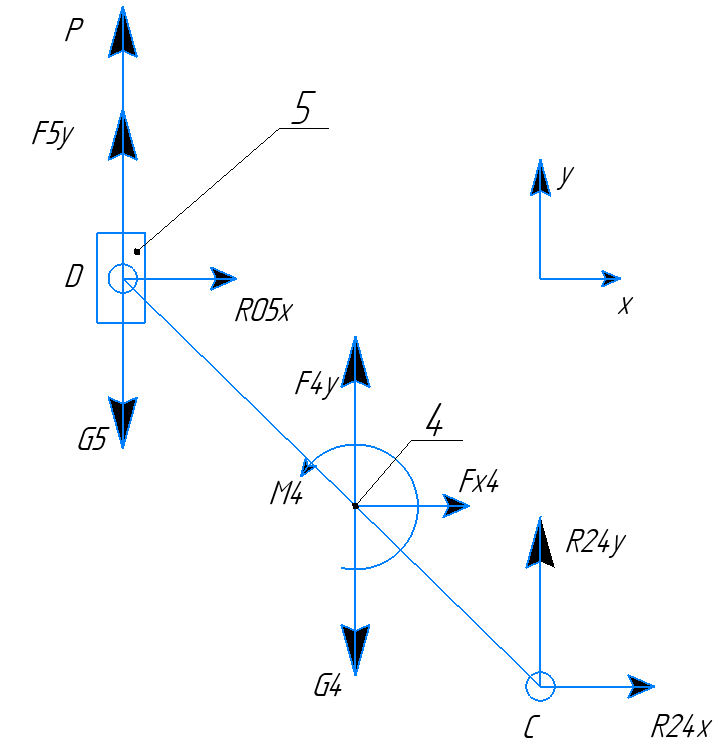
Рисунок 3. 17

Спроецируем все силы на ось x, y и сумма всех моментов относительно т.D:

Из второго уравнения выражаем R24y, из первого уравнения выражаем R05x, из третьего уравнения R24x. Рис. 3. 18

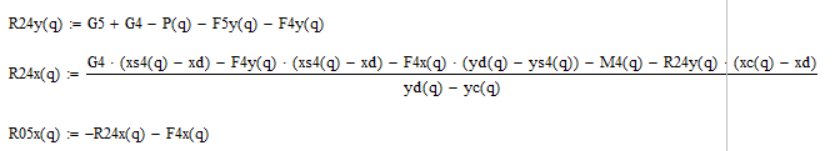
Рисунок 3. 18

Вторая структурная группа:

Расставим все силы, которые будут действовать на звенья 2 и 3. Рисунок 3.19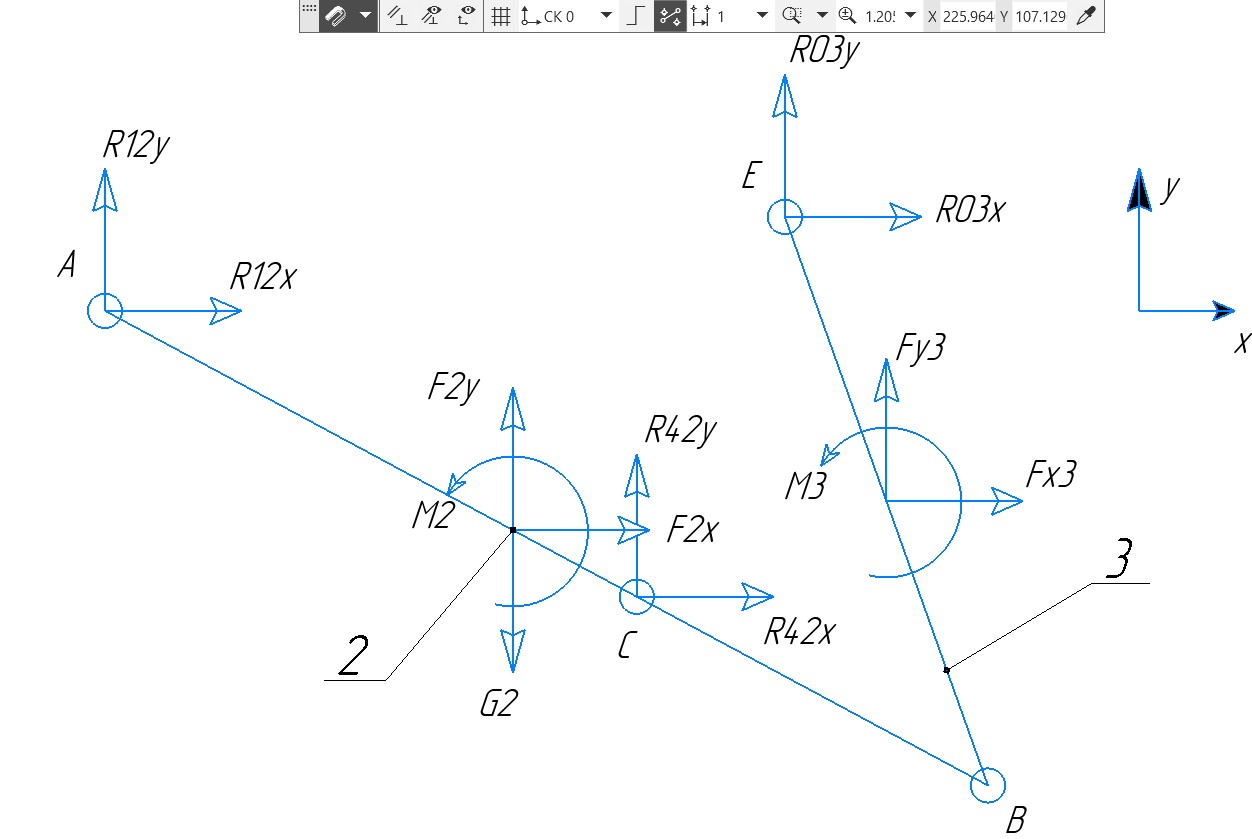

Рисунок 3. 19

Силы реакции R24x и R24y будут равнять силам реакции со стороны звена 2 на звено 4 с противоположным знаком.

Спроецируем все силы на ось x, y, сумма всех моментов относительно т. В для А и сумма всех моментов относительно т. В для Е:

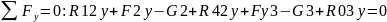
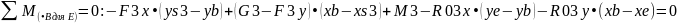
Полужирным цветом выделены неизвестные в уравнениях. Как видно из уравнений, у нас 4 уравнения, в каждом из которых по две неизвестные. Воспользуемся системой Крамера.

Для этого перенесём известные слагаемые в правую часть уравнения, в неизвестные оставим слева и обозначим их, как A1, A2, A3, A4. Рис. 3.20

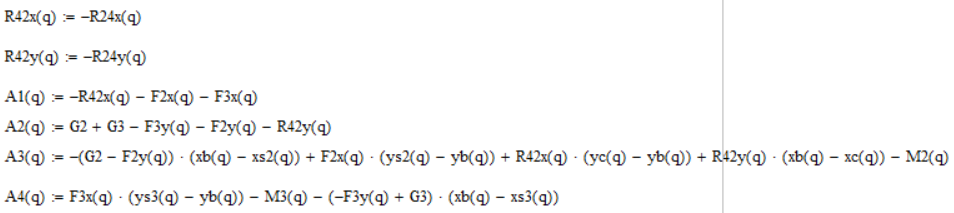
Рисунок 3. 20

Составим матрицы, для каждой неизвестной по методу Крамера. Рис. 3.21

Рисунок 3. 21

Первая структурная группа:

Расставим все силы, которые будут действовать на звено 1. Рисунок 3. 22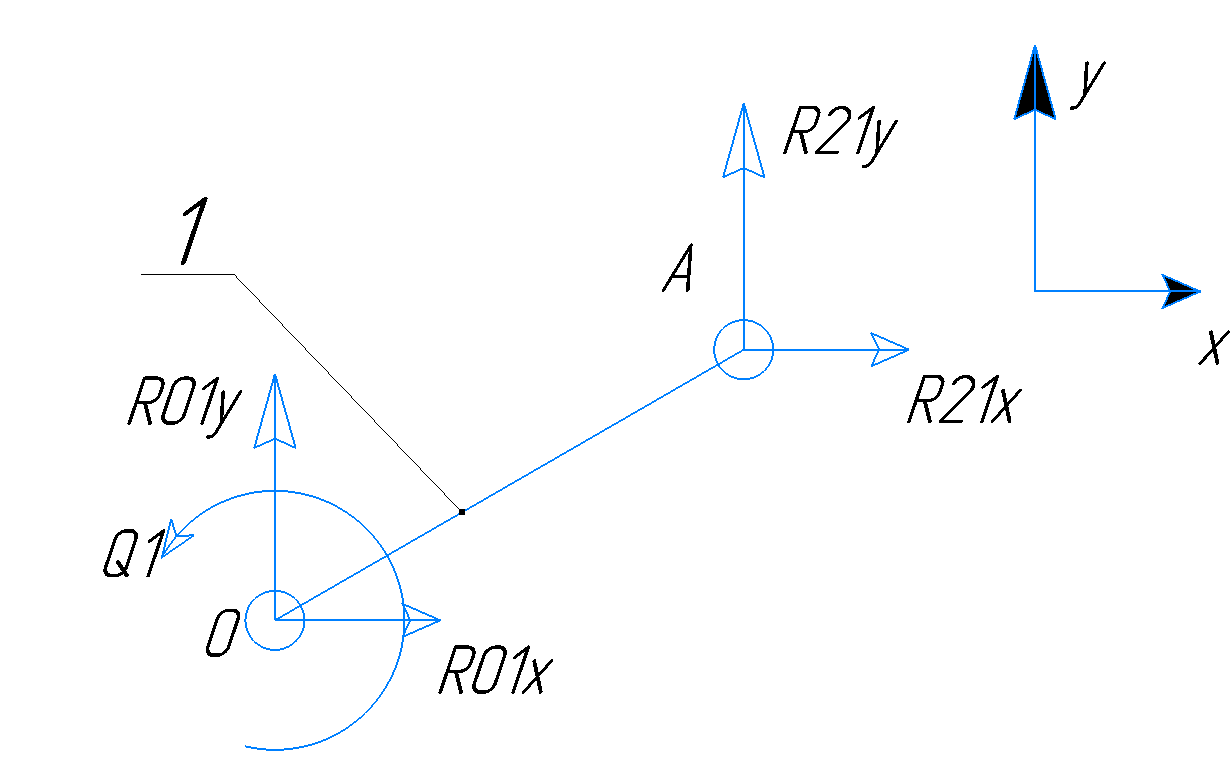

Рисунок 3. 22

Силы реакции R21x и R21y будут равнять силам реакции со стороны звена 2 на звено 1 с противоположным знаком.

Спроецируем все силы на ось x, y и сумму всех моментов относительно т. О:

Из второго уравнения выражаем R01y, из первого уравнения выражаем R01x, из третьего уравнения Q1. Рис. 3. 23

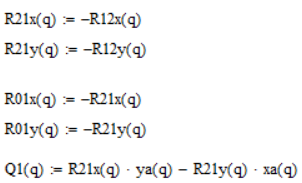
Рисунок 3. 23

Таким образом, мы с помощью уравнений кинетостатики кривошипа определили движущий момент (Q1).

3.5 Нахождение движущего момента с помощью общего уравнения динамики (уравнения Лагранжа-Даламбера).

Для нахождения движущего момента с помощью уравнения Лагранжа-Даламбера используем силы тяжести, силы инерции. Силы реакции к каждому звену компенсируются, поэтому мы их не учитываем. Рис. 3. 24

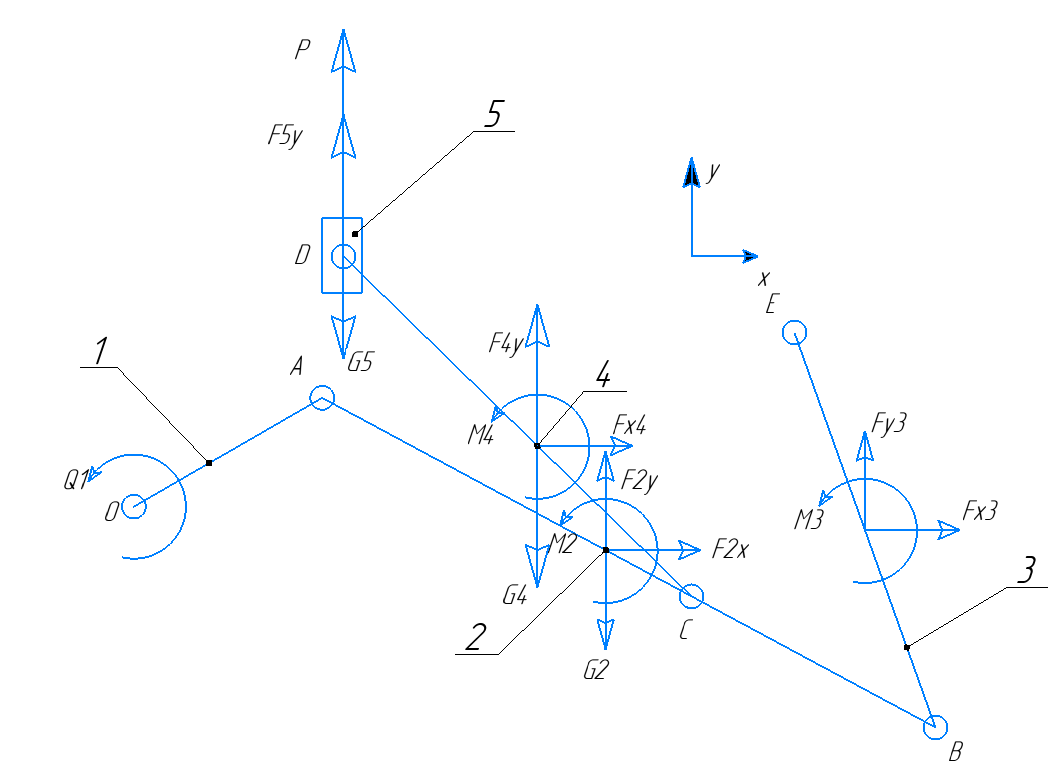
Рисунок 3. 24

Запишем уравнения Лагранжа-Даламбера для механизма:

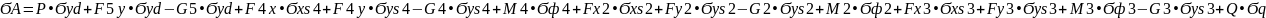
Продифференцируем уравнение по входной координате (Рис. 3.25):

Рисунок 3. 25

3.6 Сравнение найденных движущий моментов.

Можем сравнить найденные движущие моменты, которые получили двумя способами: уравнений кинетостатики и уравнения Лагранжа-Даламбера. Построим единый график, на который вынесем оба движущего момента. Рис. 3. 26

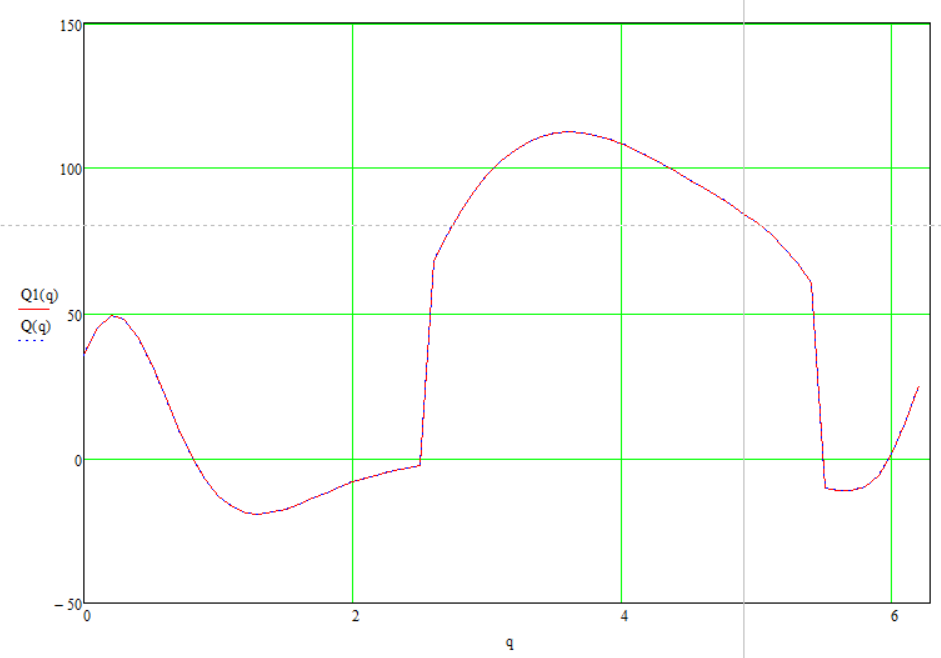
Рисунок 3. 26

Как видно из графика, оба метода совпадают. Значит все наши вычисления верны. Теперь, мы можем найти все силы.

3.7 Результаты силового расчёта

Исходя из всех вычисленных уравнений и проверки, мы можем найти все переменные в силовом расчёте. Рис. 3. 27.

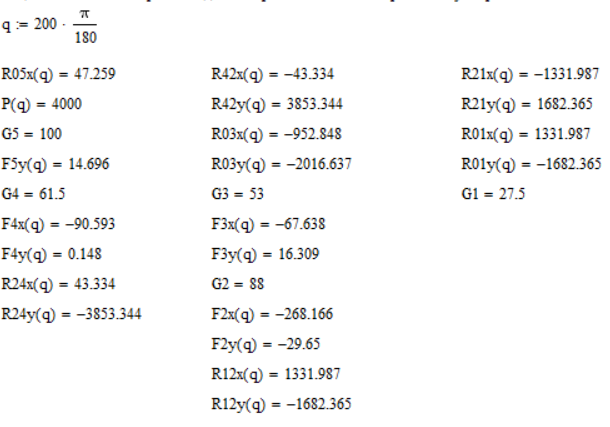
Рисунок 3. 27

4. Внешняя выиброактивность

4.1 Оценка внешней виброактивности рычажных механизмов

Определим проекции главного вектора сил инерции механизма путём суммирования соответствующих проекций отдельных звеньев (Рис. 4. 1):

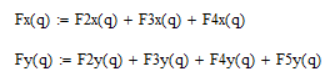
Рисунок 4. 1

Теперь мы можем построить годограф главного вектора сил инерции без уравновешивания в одном масштабе (Рис. 4. 2):

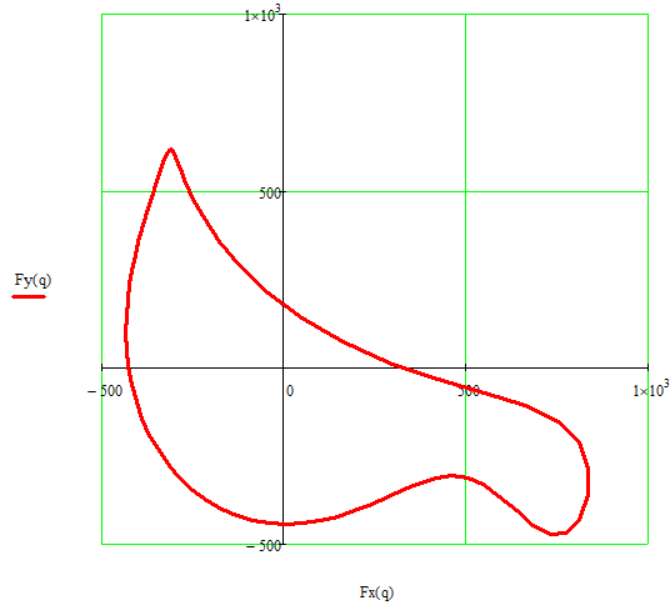
Рисунок 4. 2

4.2 Вычисление коэффициентов ряда Фурье для главного вектора сил инерци

Для этого разложим проекции главного вектора сил инерции в ряд Фурье с точностью до пяти гармоник и определим коэффициенты ряда (Рис. 4.3):

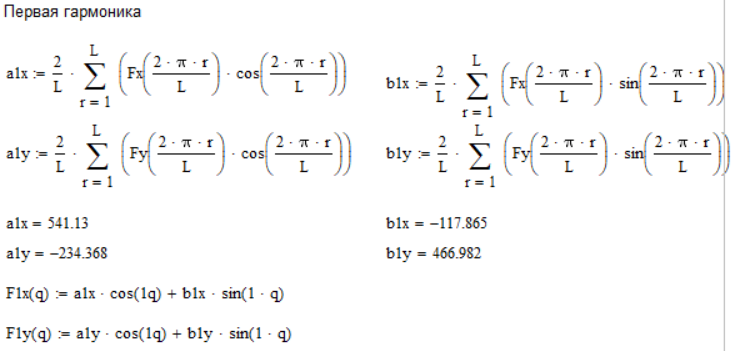
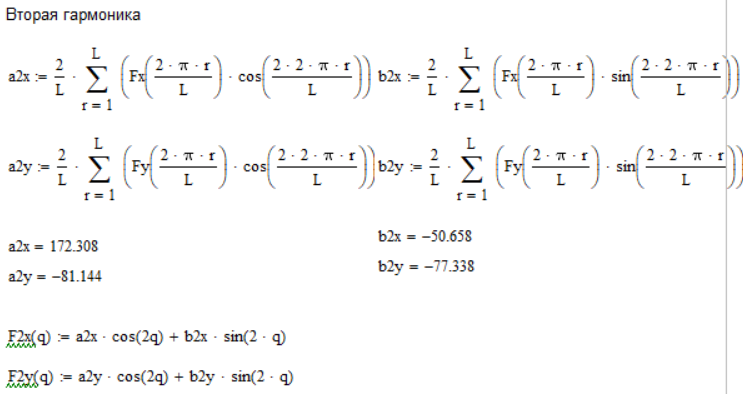
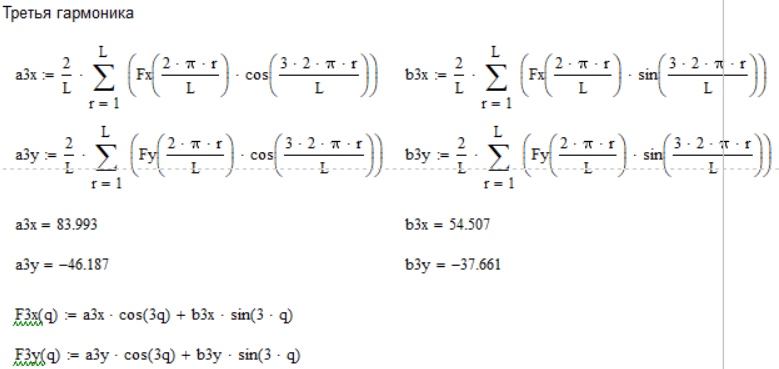
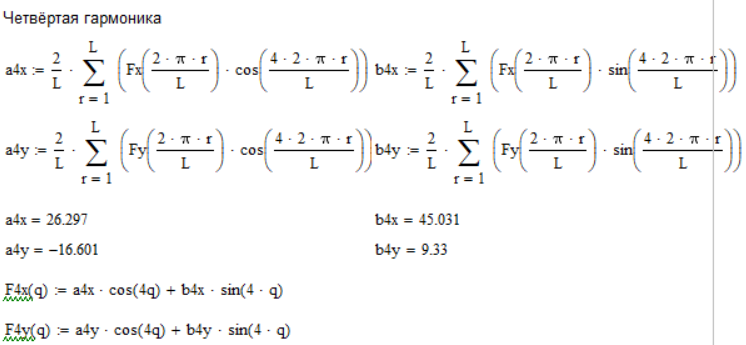
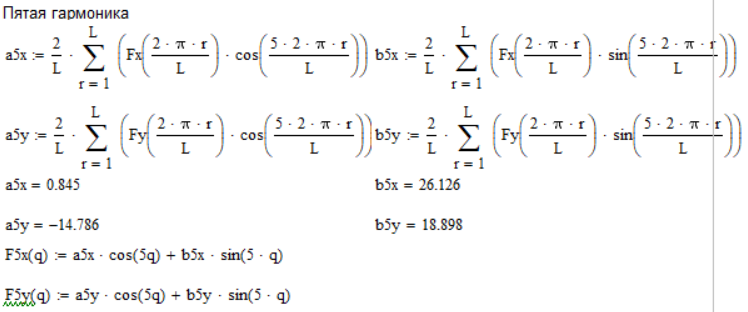
Рисунок 4. 3

4.3 Нахождение наибелее “опасной” гармоники.

Исходя из составленных пяти грамоник и нахождения их коэффицинетов, мы можем построить общий график всех гармоник для выявления наиболее “опасной”.

Для этого мы воспользуемся уравнениями, которые мы записали выше для каждой гармоники (Fix, Fiy). Общая формула представлена на рисунке 4. 4.

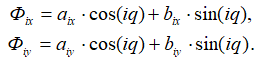
Рисунок 4. 4

Теперь мы можем построить общий график всех пяти гармоник. Рис.4. 5:

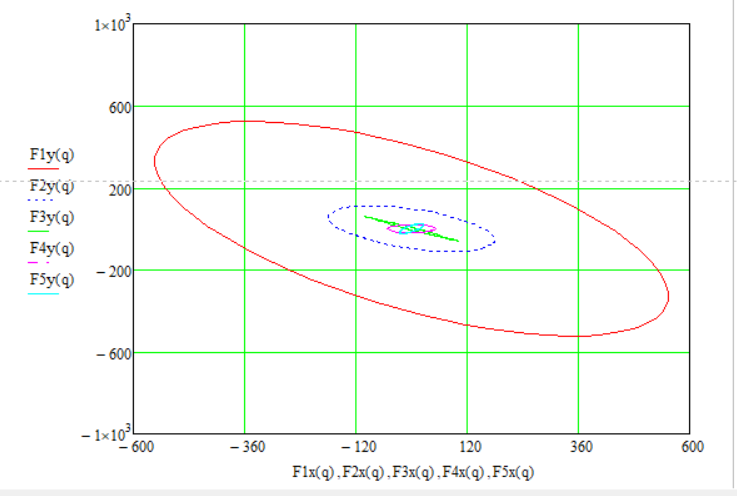
Рисунок 4. 5

Как видно из графика и самих коэффициентов гармоник, наиболее “опасной” является первая гармоника. Поэтому мы должны уравновешивать первую гармонику. Но процесс раскладывания гармоники на две окружности проведём для каждой из пяти.