12.3.Решение уравнений движения ма
Система дифференциальных уравнений движения (1) и (2) содержит две неизвестные функции времени q(t) и Q(t) . Для отыскания стационарного решения этих уравнений воспользуемся методом последовательных приближений. Для этого уравнения запишем в такой форме, чтобы в правых частях стояли только те слагаемые, которые явно содержат q , поскольку они вызывают отклонения закона движения от программного (равномерного) вращения.
где волнистой линией обозначены переменные части соответствующих функций.
В нулевом приближении, т.е. при k=0 получаем систему уравнений:
τ
Решение этой системы уравнений будем искать в виде:
После подстановки получим:
Поскольку
,
а
,
то определим среднюю угловую скорость
входного звена и средний движущий
момент:
При k=1 получим систему уравнений:
Выражение, стоящее в правой части первого уравнения характеризует возмущение, вызывающее отклонение закона движения входного звена (кривошипа) от программного (равномерного) вращения.
Возмущающий момент характеризует внутреннюю виброактивность исполнительного механизма.
Решение системы уравнений в первом приближении (k=1) разыскиваем в виде:
Здесь
ψ(t)
- отклонение закона движения входного
звена от программного (равномерного)
движения, называемое динамической
ошибкой по углу;
-
отклонение движущего момента от среднего
значения.
Подставив эти решения в систему уравнений, получим:
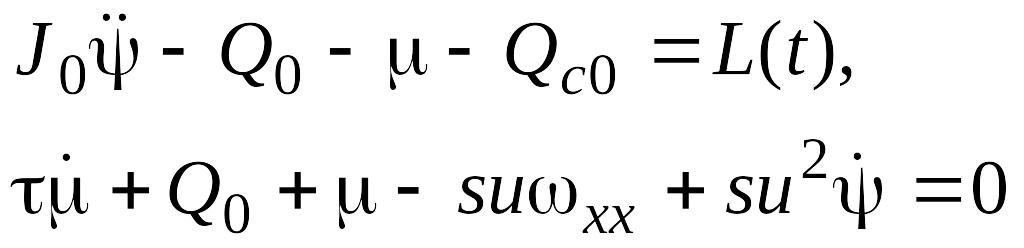
Или
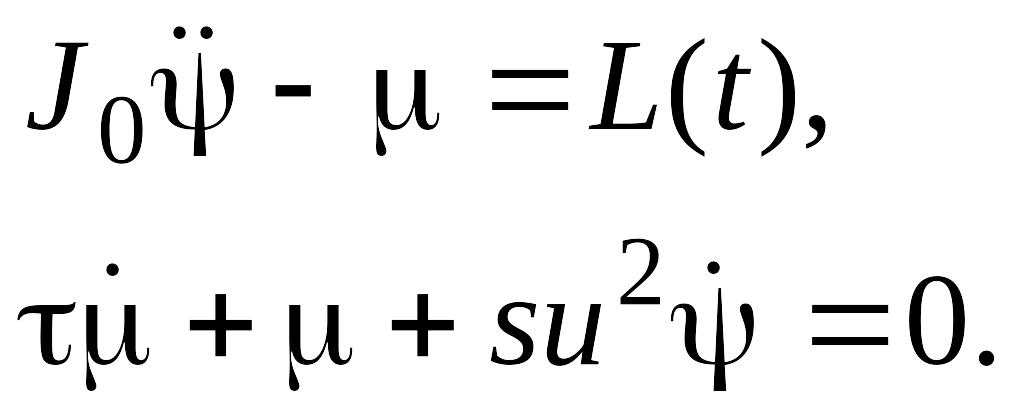
Перепишем эти уравнения в операторном виде (p=d/dt):
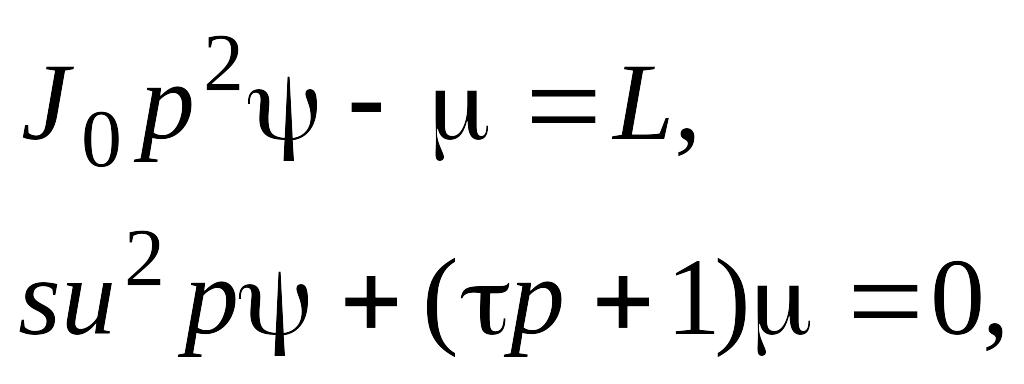
откуда найдем
где τm - механическая постоянная времени машины :
Разложим возмущающий момент на программном движении q(0)=ω0t в ряд Фурье с точностью до пяти гармоник:
;
.
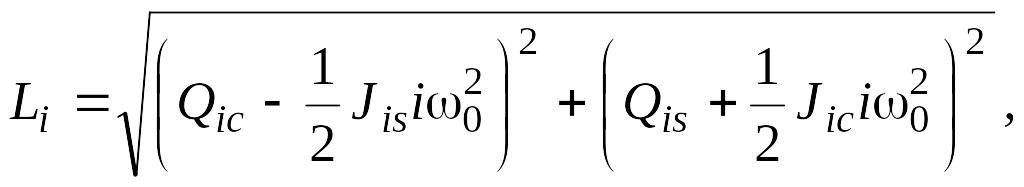
Разложение возмущающего момента в ряд Фурье:
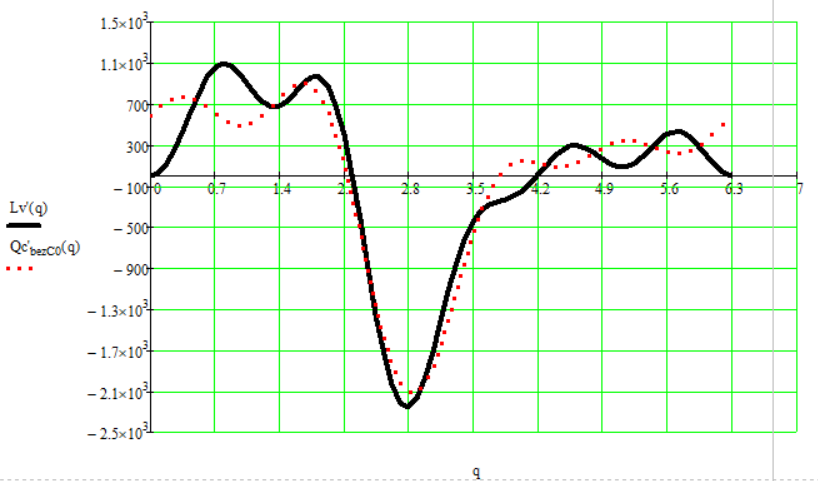
Рис. 12.6. График возмущающего момента
Далее найдем динамическую ошибку по углу с точностью до пяти гармоник:
где
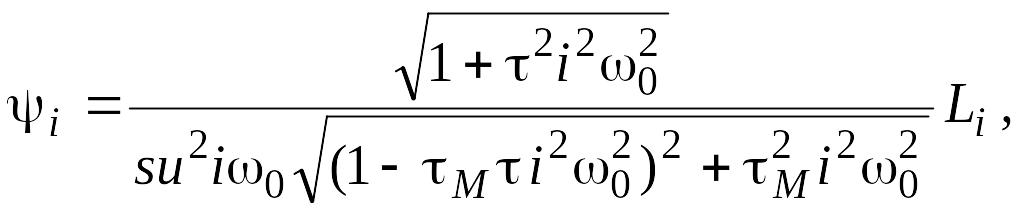
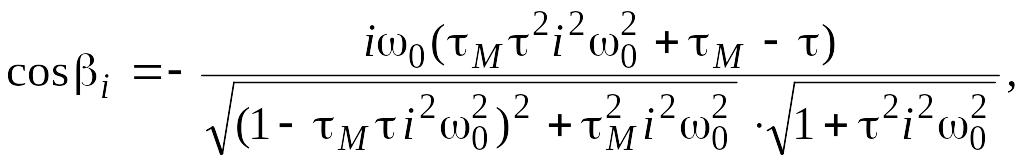
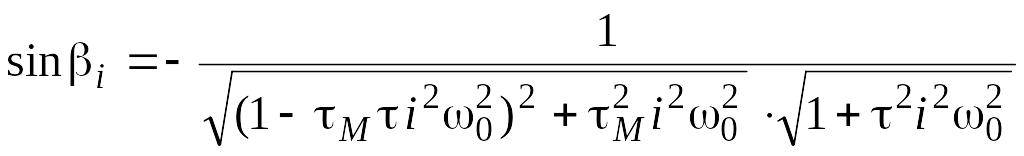
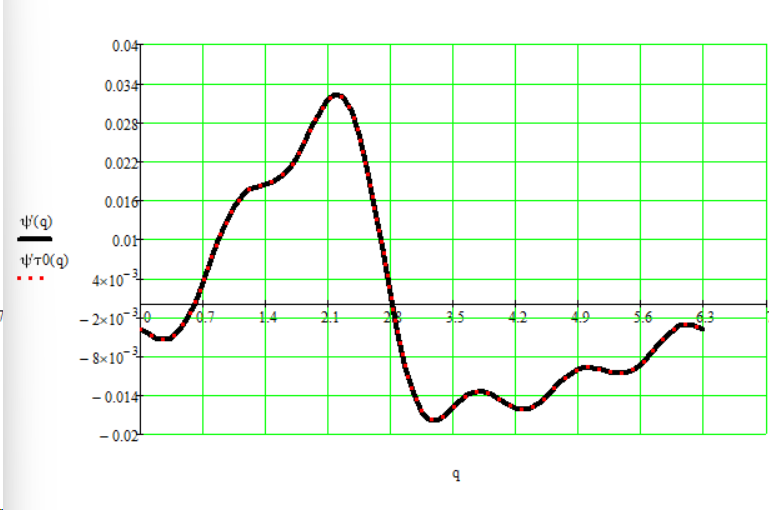
Рис. 12.7. График динамической ошибки по углу.
Найдем динамическую ошибку по скорости:
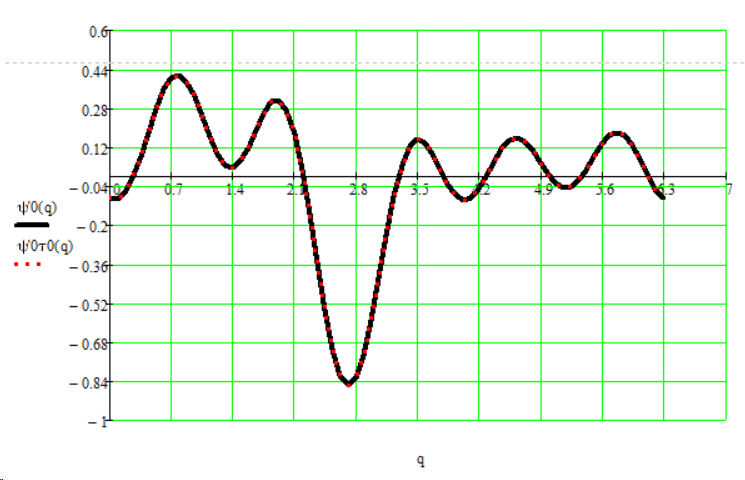
Рис. 12.8. График динамической ошибки по скорости.
Определение коэффициента неравномерности вращения входного звена:
Неравномерность вращения ротора двигателя принято характеризовать коэффициентом неравномерности вращения.
Сама по себе неравномерность вращения, как правило, не влияет на качество рабочего процесса. Чаще всего она опасна тем, что вызывает дополнительные потери энергии в двигателе и повышенные динамические нагрузки в передаточном механизме.
Кроме того неравномерность вращения ротора двигателя обладающего обычно большим моментом инерции вызывает динамические воздействия на основания.
По графику динамической ошибки по скорости найдем максимальные значения ошибки для того, чтобы рассчитать коэффициент неравномерности вращения:
Рассчитаем коэффициент неравномерности вращения:
Значение не превышает допустимое, данное в задании
и равное 0.15, значит не требуется производить улучшения динамических характеристик.
Найдем механическую характеристику двигателя с точностью до пяти гармоник:
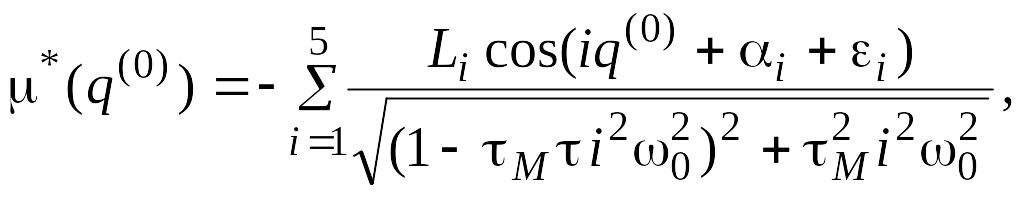
где
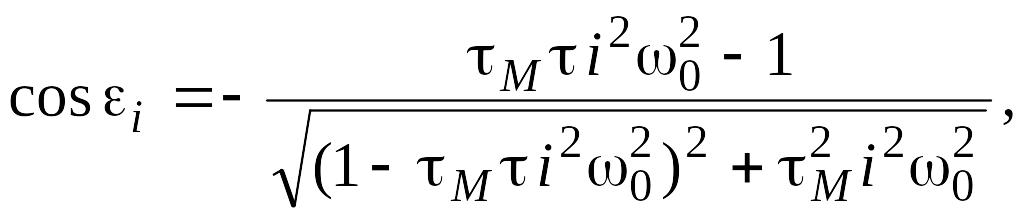
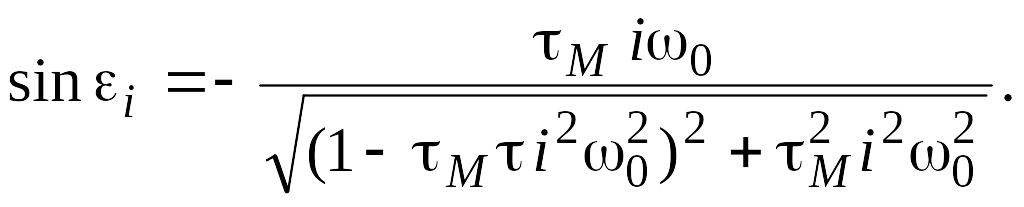
Тогда закон изменения движущего момента при учете механической характеристики двигателя с точностью до пяти гармоник определяется по формуле:
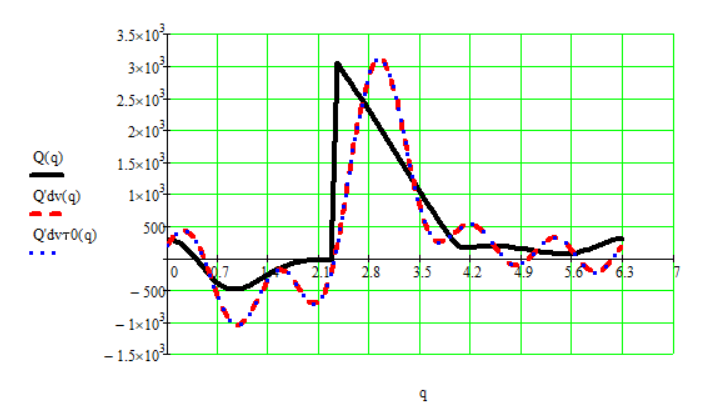
Рис. 12.9. График движущего момента при динамическом расчете, разложенный в ряд Фурье.